机器学习周记（第三十三周：文献阅读[GWO-GART]）2024.4.1~2024.4.7

本文主要是介绍机器学习周记（第三十三周：文献阅读[GWO-GART]）2024.4.1~2024.4.7，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

摘要

ABSTRACT

1 论文信息

1.1 论文标题

1.2 论文摘要

1.3 论文数据集

1.4 论文模型

2 相关知识

摘要

本周阅读了一篇使用GAT结合GRU预测PM2.5浓度的文章。论文模型为图注意力循环网络（GART），首次提出了一种新型的多层GAT架构，可以循环地提取城市的空间特征，并获取城市之间更多的隐含关联。其次，利用灰狼优化（GWO）来选择模型的最佳超参数集。这种自动化方法有助于优化GART的网络结构。

ABSTRACT

This week, We read a paper on predicting PM2.5 concentration using Graph Attention Network (GAT) combined with Gated Recurrent Unit (GRU). The model proposed in the paper is called Graph Attention Recurrent Network (GART), which introduces a novel multi-layer GAT architecture for cyclic extraction of spatial features of cities, thereby capturing more implicit associations between cities. Furthermore, Grey Wolf Optimization (GWO) is employed to select the optimal set of hyperparameters for the model. This automated approach aids in optimizing the network structure of GART.

1 论文信息

1.1 论文标题

A long-term prediction method for PM2.5 concentration based on spatiotemporal graph attention recurrent neural network and grey wolf optimization algorithm

1.2 论文摘要

随着全球工业化和城市化的迅速发展，空气污染问题变得日益严重，主要以PM2.5作为主要污染成分，直接影响了人们的健康。因此，对长期PM2.5水平进行预测是非常有必要的。然而，大多数现有的PM2.5浓度预测方法缺乏足够的提取城市空间特征的能力。因此，本文提出了一种基于时空图注意力循环神经网络和灰狼优化（GWO-GART）的新方法。首先，通过使用图注意力网络（GAT）、图神经网络（GNN）和门控循环单元（GRU）构建了一个PM2.5的长期预测模型，称为图注意力循环网络（GART）。在GART模型中，首次提出了一种新型的多层GAT架构，可以循环地提取城市的空间特征，并获取城市之间更多的隐含关联。其次，利用灰狼优化（GWO）来选择模型的最佳超参数集。这种自动化方法有助于设计GART的网络结构。最后利用从现实世界收集的数据集将GWO-GART与三种单一模型和两种混合模型进行了比较。结果显示，与最先进的模型（SOTA）相比，GWO-GART在所有数据集上的均方根误差（RMSE）平均减少了2.13％，平均绝对误差（MAE）减少了2.47％，临界成功指数（CSI）平均增加了1.55％。这表明，GWO-GART提供了一种切实有效的方法，可以准确预测城市地区的长期PM2.5水平。

1.3 论文数据集

本文选取中国184个城市区域进行PM2.5浓度预测研究，如Fig.1所示。大气污染受环境因素和地理因素的影响，包括空气湿度、地表温度、降水、大气压等。而且，特定位置的空气污染水平不仅受到当地排放的影响，还受到邻近地区污染的影响。以京津冀地区为例，北京PM2.5浓度受到天津、廊坊等多个地区工业排放的影响。因此，工厂排放的空气污染物的扩散往往受到地理因素的影响，如地点之间的距离、海拔差异、高山、强气流和风向等。为了充分考虑这些因素对PM2.5浓度沉降和扩散的影响，将每个城市节点的属性值由8个气象和环境数据组成，包括：海拔高度、k指数、经度风分量U、纬度风分量V、相对湿度、2m处地面温度、大气压和总降水量。具体数据统计如Table1所示。

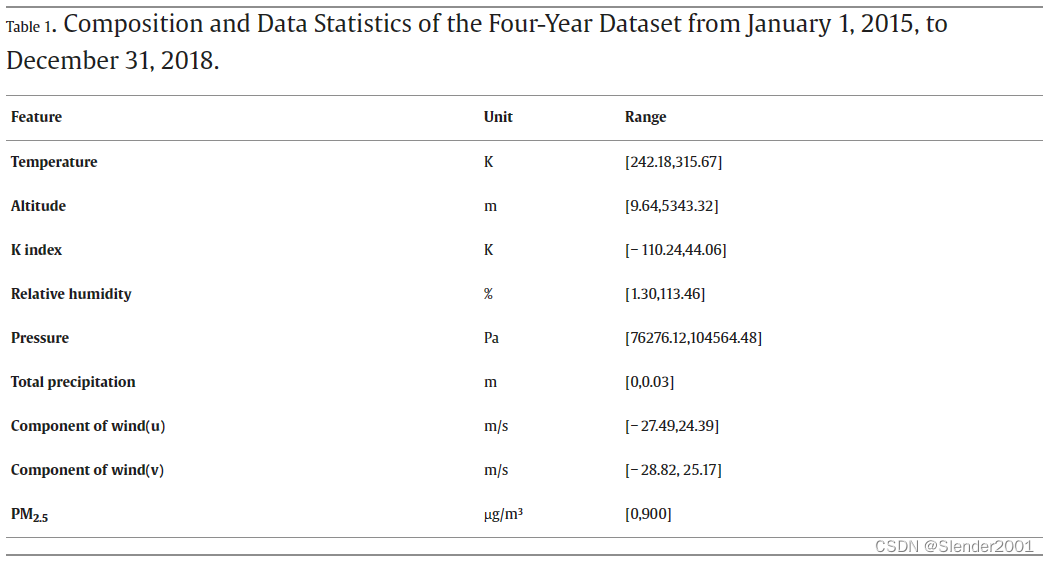
每个城市的PM2.5浓度数据来自生态环境部（MEE），而气象和环境指标则来自ERA5大气再分析数据集。这些指标通过热力学效应与PM2.5的垂直扩散动态相关。连接相邻城市节点的边的属性包括以下6个因素：两个城市节点之间的距离（ $d$ ）；起始城市节点风速（ $v$ ）；从起始城市到目标城市的方向（ $\gamma$ ）；起始城市节点风向（ $\beta$ ）；水平扩散系数（ $S$ ）；注意力系数（ $Y$ ）。这些因素与PM2.5的水平扩散有关。水平扩散系数S的计算公式如Eq.(1)所示。

$S=ReLU(\frac{\left | v \right |}{d} \cos (\left | \gamma -\beta \right |))$ (1)

1.4 论文模型

论文模型（GWO-GART），如Fig.2所示，主要由两部分组成：(1).GART预测模型，主要由多层GAT、多层GNN以及一个GRU层组成。在GART中，空间特征通过多层GAT提取，而气象环境特征通过多层GNN提取。接着，将被提取的多个特征通过特征融合连接起来，GRU层进一步捕获数据的时间特征。(2).灰狼优化算法（GWO），用于优化GART的网络结构。

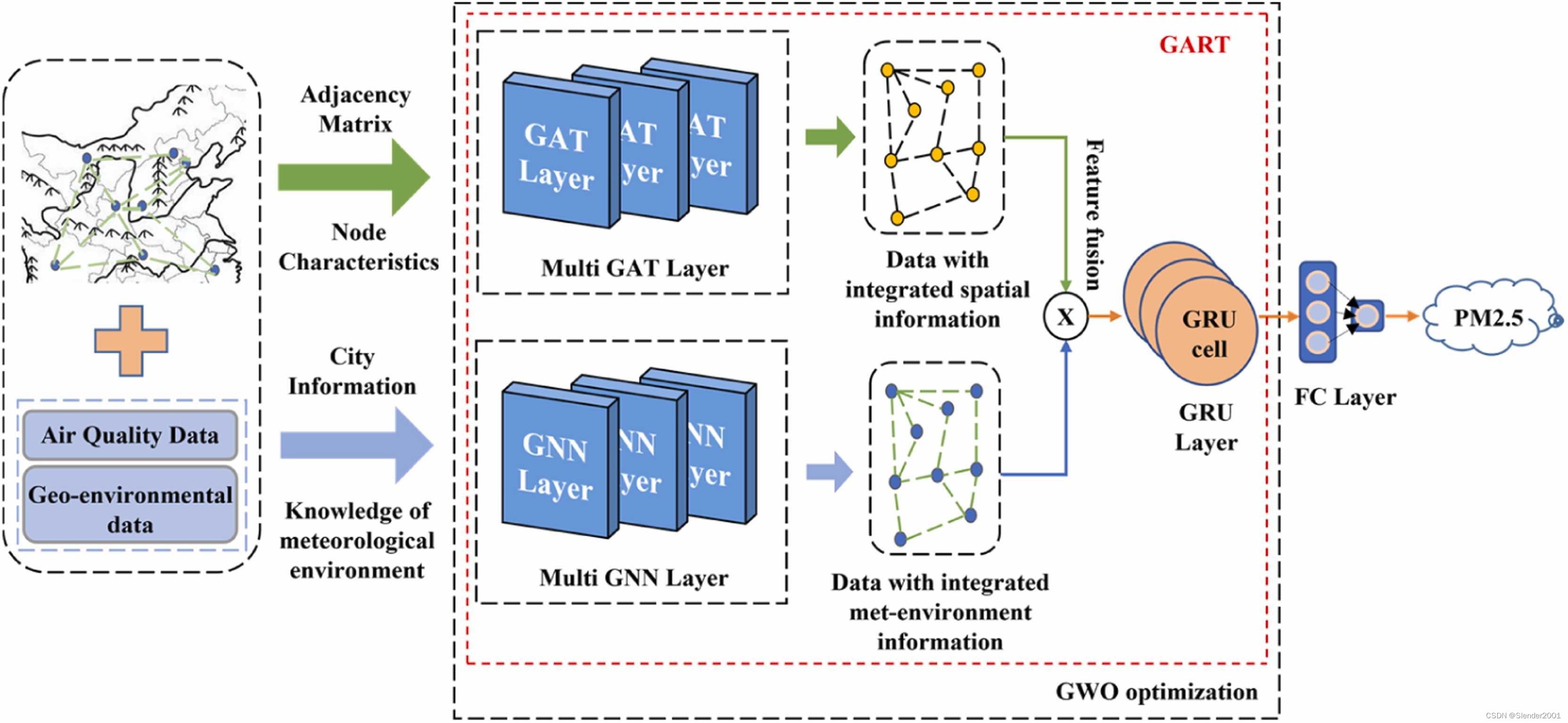
利用数据集提供的184个城市的空气质量数据、地理环境数据和经纬度信息，构建了城市的图结构和邻接矩阵。PM2.5等空气污染物的水平迁移随着两地距离的增加而减少。同样，在两个地点之间存在大量高海拔山脉也会影响空气污染物的水平迁移。因此，基于这两个视角构建邻接矩阵。通过查询城市的经纬度信息，如果两个节点之间的欧氏距离大于300公里，或者节点之间有3座及以上海拔超过1200米的山脉，则认为节点之间没有边。邻接矩阵的具体约束如Eq.(2)、Eq.(3)、Eq.(4)所示。

$d_{ij}=\left \| \alpha _{i}-\alpha _{j} \right \|$ (2)

$m_{ij}=sup\left \{ h(\lambda \alpha _{i} + (1-\lambda )\alpha _{j}) - \max \left \{ h(\alpha _{i}),h(\alpha _{j}) \right \} \right \},\lambda \in (0,1)$ (3)

$A_{ij}=H(d_{T}-d_{ij}) \cdot H(m_{T}-m_{ij})$ (4)

节点的地理坐标用 $\alpha$ 表示，高度用 $h(\alpha )$ 表示。 $m_{ij}$ 表示节点 $i$ 和节点 $j$ 之间的山脉中的最大高度差。符号 $\left \| \cdot \right \|$ 表示向量的L2范数， $d_{ij}$ 表示两个节点之间的欧氏距离。 $d_{T}$ 为距离阈值（300km）， $m_{T}$ 为高度阈值(1200m)。 $H(\cdot)$ 是赫维赛德函数，只有当 $x>0$ 时，其值为1，否则为0。

构建邻接矩阵后，两个节点之间具有非零值的节点称为邻接节点，共有3938组，这意味着整个城市图有3938条边。分别计算这些边对应的属性，形成城市信息，用于后续的水平扩散系数S和注意力系数Y的计算。

GART模型将组织好的城市信息和气象环境知识作为多层GNN的输入，充分提取气象环境数据的特征。其目标是输出融合气象和环境知识特征的融合数据。另外，基于邻接矩阵和节点特征，GART将其输入到多层GAT中提取PM2.5的空间特征。它的输出融合了空间特征的数据。然后，模型对上述两类数据进行特征融合。融合后的数据通过GRU层来反映PM2.5在时间序列上的沉积和消散，从而提取时间维度上的长期特征。为了紧密融合不同特征信息，采用全连接层将数据降维为一维。这代表了PM2.5的最终预测值。GWO通过参数组合对GART预测模型进行进一步优化，得到GWO-GART预测模型。GWO改善了多个模型之间的兼容性，增强了模型的预测精度。

GART模型采用多层GNN和MLP层融合气象和环境知识，如Fig.3所示。在Fig.3中，当预测时间 $t$ 的PM2.5浓度时，输入包括气象数据 $O^{t}$ 、节点的城市信息 $G^{t}$ ，以及上一个时间步的历史PM2.5数据 $P^{t-1}$ 。经过多层GNN的处理后，得到了一个包含气象和环境特征的融合向量 $X^{t}$ 作为输出。接下来， $X^{t}$ 被用作后续步骤中下一个GNN层的输入。通过所有GNN层融合气象和环境知识后，采用两个MLP层。第一个MLP层将输入特征向量 $X^{t+n}$ 的维度从低维度增加到高维度，而第二个MLP层将这个高维向量的维度降低。这使得不同特征向量之间的信息融合，并且使模型能够获得更全面的表达能力。最终输出 $X^{out}$ 代表了气象和环境知识的融合。

计算公式如下：

$X^{t}=\textup{GNN}(O^{t},P^{t-1},G^{t})$

$X^{t+1}=\textup{GNN}(O^{t+1},P^{t},G^{t+1},X^{t})$

$...$

$X^{t+n}=\textup{GNN}(O^{t+n},P^{t+n-1},G^{t+n},X^{t+n-1})$

$X^{out}=\textup{MLP}_{2}(\textup{MLP}_{1}(X^{t+n}))$ (5)

气象数据 $O^{t}$ 包括12个特征，其中包括城市节点在时间 $t$ 的8个气象和环境特征，两个时间特征，以及风速特征和风向特征。城市信息 $G^{t}$ 包括在时间 $t$ 的3938条边的属性信息以及基于边属性计算的水平扩散系数S。

在PM2.5的长期预测中，空间特征的提取至关重要，它反映了城市节点之间的邻接关系，并包含了城市图的空间特征。本文提出了一种多层GAT循环网络，如Fig.4所示。它不仅考虑了每一层的当前输入，还考虑了前一层GAT输出的影响。通过多层GAT完全提取邻接矩阵中隐含的空间信息，也是该模型功能的关键组成部分之一。多层图注意力（Multi-GAT）如Fig.4所示。在时间 $t$ ，GAT 将节点特征 $F^{t}$ 和邻接矩阵 $A$ 作为输入。GAT的输出是注意力系数 $Y^{t}$ 。 $F^{t}$ 包括八个气象和环境特征，这些节点特征随时间变化。 $A$ 是一个184×184维的矩阵，涵盖了所有城市节点之间的空间关系。多层图注意力循环网络通过为每条边计算注意力系数来量化空间关系的强度。

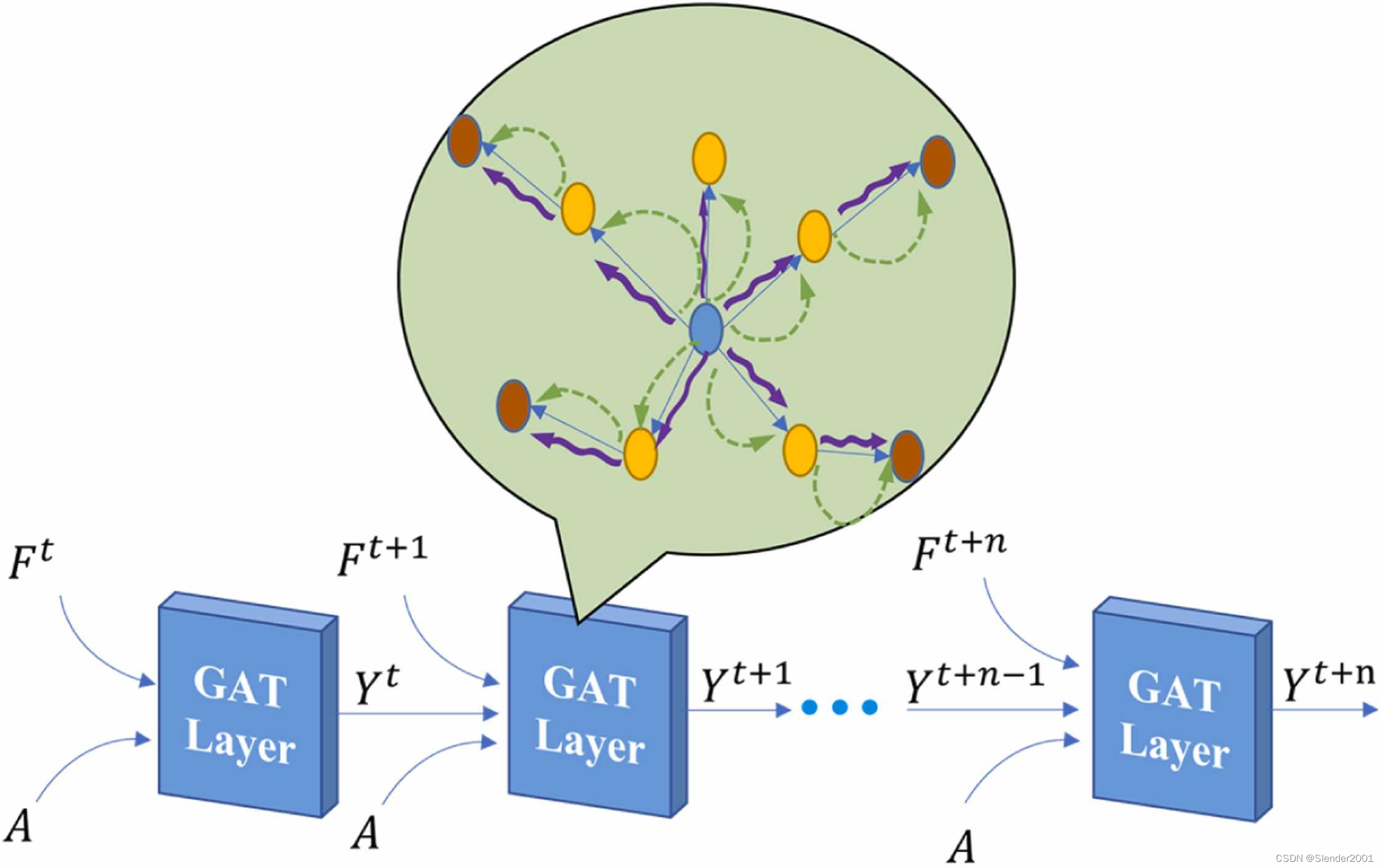
具体计算过程如Eq.(6)所示：

$Y^{t}_{ij}=\frac{\textup{ln}(LeakyReLU(a\left [ WF^{t}_{i} \left | \right | WF^{t}_{j} \right ]))}{\sum_{j\in N_{i}}^{}\textup{ln}(LeakyReLU(a\left [ WF^{t}_{i} \left | \right | WF^{t}_{k} \right ]))}$ (6)

其中， $N_{i}$ 代表节点 $i$ 的所有邻居节点， $j$ 是 $N_{i}$ 中的一个节点； $F^{t}$ 表示时间 $t$ 的节点特征； $W$ 是用于不同节点的共享参数矩阵； $W\cdot F^{t}$ 是两个向量的内积运算； $\cdot ||\cdot$ 表示在增加节点维度后的连接操作； $a(\cdot)$ 是用于减小连接后高维向量维度的单层前馈神经网络； $W$ 和 $a(\cdot)$ 都是方程中的可学习参数。注意力系数Y经过归一化处理，如Eq.(7)所示，其中使用LeakyReLU激活函数以保留节点自身的特征信息，并防止在计算过程中被丢弃。然后， $Y^{t}$ 作为下一层GAT的输入，参与后续的计算。

具体计算过程如Eq.(7)所示：

$Y^{t}=\textup{GAT}(F^{t},A)$

$Y^{t+1}=\textup{GAT}(F^{t+1},A,Y^{t})$

$...$

$Y^{t+n}=\textup{GAT}(F^{t+n},A,Y^{t+n-1})$ (7)

从Eq.(7)可以观察到，空间依赖关系随着时间变化，因为多层GAT在计算下一个时间步的注意力系数时考虑了上一个时间步的注意力系数。而且数据是每隔3小时收集一次的，包括风速、温度、湿度和降水等特征，所有这些特征都可能发生波动，进而影响PM2.5的扩散。这些特征变化也受到上一个时间步的影响，这就是本文采用循环方法更有效地提取空间依赖关系的原因。模型将传统的图注意力网络转换为类似于RNN的循环结构，目的是适应这些特征的变化。

在计算完注意力系数后，通过聚合所有邻居节点的信息来更新节点自身的特征 $F{}'$ ，如Eq.(8)所示。

$F{}'_{i}=\sigma (\sum_{j\in N_{i}}^{}Y^{t}_{j}WF^{t}_{i})$ (8)

其中， $N_{i}$ 是与中心城市 $i$ 相邻的城市集合，而 $j$ 是其中的任意一个相邻城市。 $Y^{t}_{j}$ 表示时间 $t$ 时城市 $i$ 和 $j$ 之间的注意力系数。 $W$ 是共享参数矩阵，而 $F^{t}_{i}$ 表示时间 $t$ 时城市 $i$ 的节点特征。Eq.(8)表示将城市之间的注意力系数视为权重系数，反映了相邻城市对PM2.5扩散的贡献。注意力系数越大，权重越高。根据不同的权重，所有的局部特征被聚合以更新 $i$ 的特征信息 $F{}'_{i}$ ，从而影响PM2.5的预测。

在每个GAT层中，都采用了多头注意力机制，如Fig.4中的绿色区域所示。通过多头注意力机制，模型可以使用不同的可学习参数集合集中于问题的不同方面。每个彩色箭头代表一组注意力参数，对应于Fig.4中的三头注意力机制。然后，来自多个头的注意力结果被聚合以更新节点特征。

引入了多头注意力机制后，节点信息的更新根据Eq.(9)进行。

$F{}'_{i}=\sigma (\frac{1}{K}\sum_{k=1}^{K}\sum_{j\in N_{i}}^{}Y^{t}_{j}W^{k}F^{t}_{j})$ (9)

其中， $K$ 表示注意力头的数量，每个头专注于不同的方面，可以使用 $W$ 和 $a(\cdot)$ 进行调整。在为每个头计算完注意力系数后，每个头专注于不同的方面，形成一个新的特征向量 $F{}'$ ，其中包含来自相邻节点的信息。

PM2.5浓度表现出显著的时间变化。随着时间步长的增加，不确定性增加，这使得提取PM2.5的长期时间特征变得具有挑战性。因此，在本文中，将来自相应时间段的空间特征、气象和环境特征结合起来，以改善模型在提取时间特征时的预测性能。特征融合的目的是将来自不同领域提取的特征数据集成到一个统一的表示中，从而为提取时间特征提供更全面的输入。

为了整合来自不同领域提取的特征，本文采用了多维特征串联融合，如Fig.5所示。该图描述了从时间步长 $t$ 到 $t+n$ 的特征融合过程。在时间步长 $t$ ， $X^{t}$ 表示通过多层GNN融合气象和环境知识后获得的高维数据。 $Y^{t}$ 对应于通过多头GAT提取空间特征后获得的高维数据。 $P^{t}$ 表示时间步长 $t$ 的气象和环境数据，具体包括PM2.5值和气象特征（类似于多层GNN的输入 $O^{t}$ ）。在每个时间步长，这三部分数据被串联起来形成 $N^{t}$ 。这个过程在n个时间步骤中重复进行，产生n个 $N^{t}$ 向量，对应于单个时间步骤。然后，这些n个向量再次串联起来形成高维数据 $M_{t}$ 。在完成特征串联融合后， $M_{t}$ 进一步通过GRU进行后续时间特征提取处理。

GART模型结合了多个深度学习模型，用于提取时间特征和空间特征。因此，整体模型结构变得复杂，具有大量参数和高维向量，增加了参数调整和模型优化的难度。然而，引入GWO为解决这一问题提供了有效的解决方案。

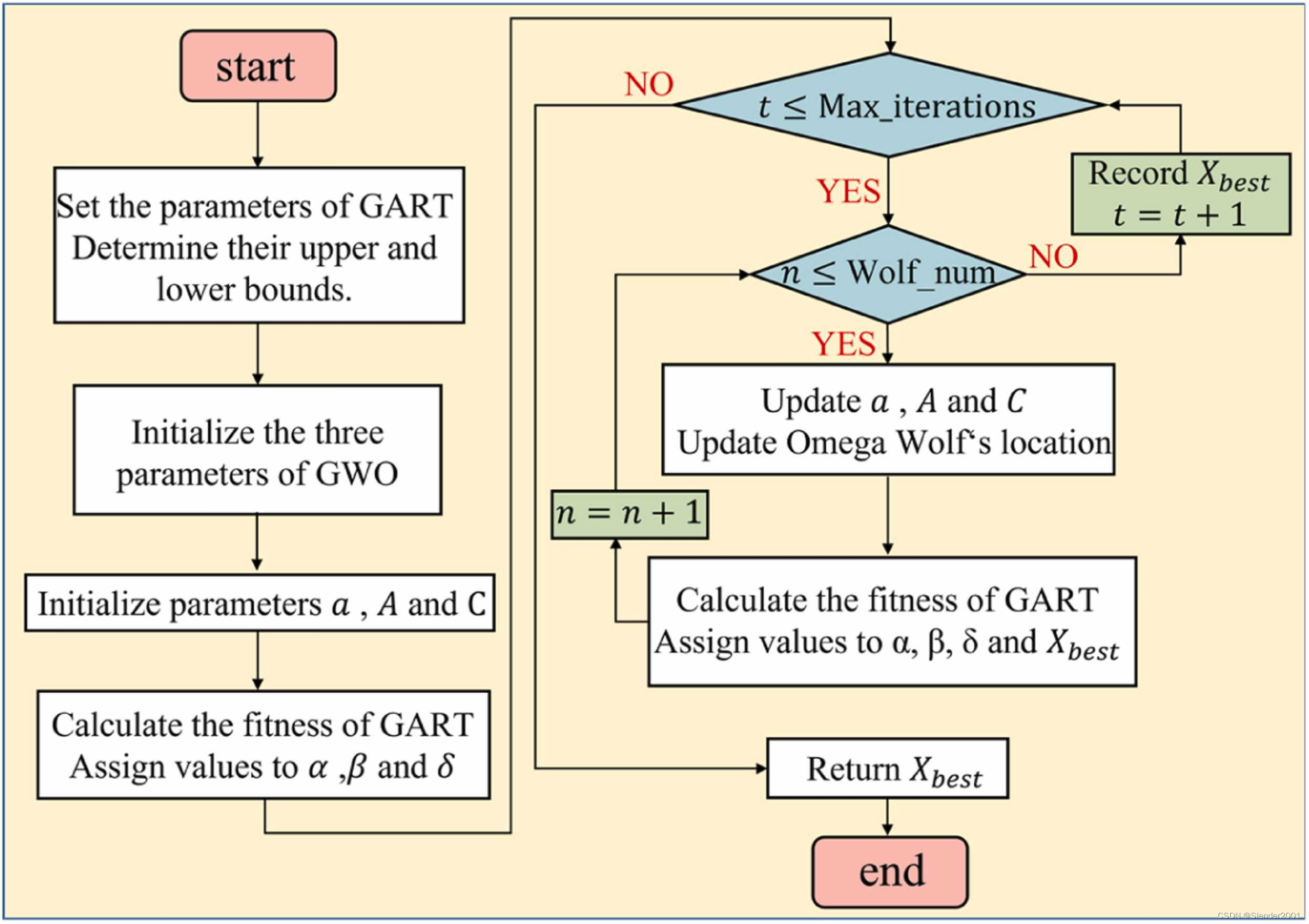
GART模型的GWO优化的主要步骤如下：

step1：定义需要优化的GART参数，并确定它们的上下边界。

step2：初始化GWO的三个参数：灰狼种群大小（Wolf_num）、要优化的参数数量（dim）和允许的最大迭代次数（Max_iterations）。

step3：初始化可训练参数a、A和C。其中，参数a的具体计算如Eq.(10)所示。

$a=\frac{2*(Max\_iterations-t)}{Max\_iterations}$ (10)

step4：计算GART的适应度，依次选择三个最低适应度值，并按升序将它们分配给α、β和δ狼。具体来说，根据step1的规定，生成适用于Wolf_num个参数组合，并将它们用作GART计算的输入。适应度由在验证集上的最佳损失值确定，其计算方式如Eq.(11)所示。

$\textup{Val}_{loss}(x_{i},x{}'_{i})=\frac{\sum_{i=1}^{n}(x_{i}-x_{i}{}')^{2}}{n}$ (11)

其中，n是城市节点的数量， $x_{i}$ 是预测的PM2.5浓度， $x_{i}{}'$ 是真实的PM2.5浓度。基于模型返回的验证集损失值进行GWO优化。较小的损失值表示更高的预测准确性，表明GWO优化过程更接近最优解。

step5：更新参数a、A和C。计算猎物与灰狼之间的距离D，然后更新Omega狼的位置，将GART参数移动到最优组合附近。

step6：根据更新后的参数，通过代入GART计算Fitness。按顺序重新分配三个最小值给α、β和δ狼，并将最小值分配给 $X_{best}$ 。

step7：迭代Max_iterations次，持续更新 $X_{best}$ 。

step8：输出GART的最佳参数组合 $X_{best}$ ，并结束GWO的优化过程。

2 相关知识

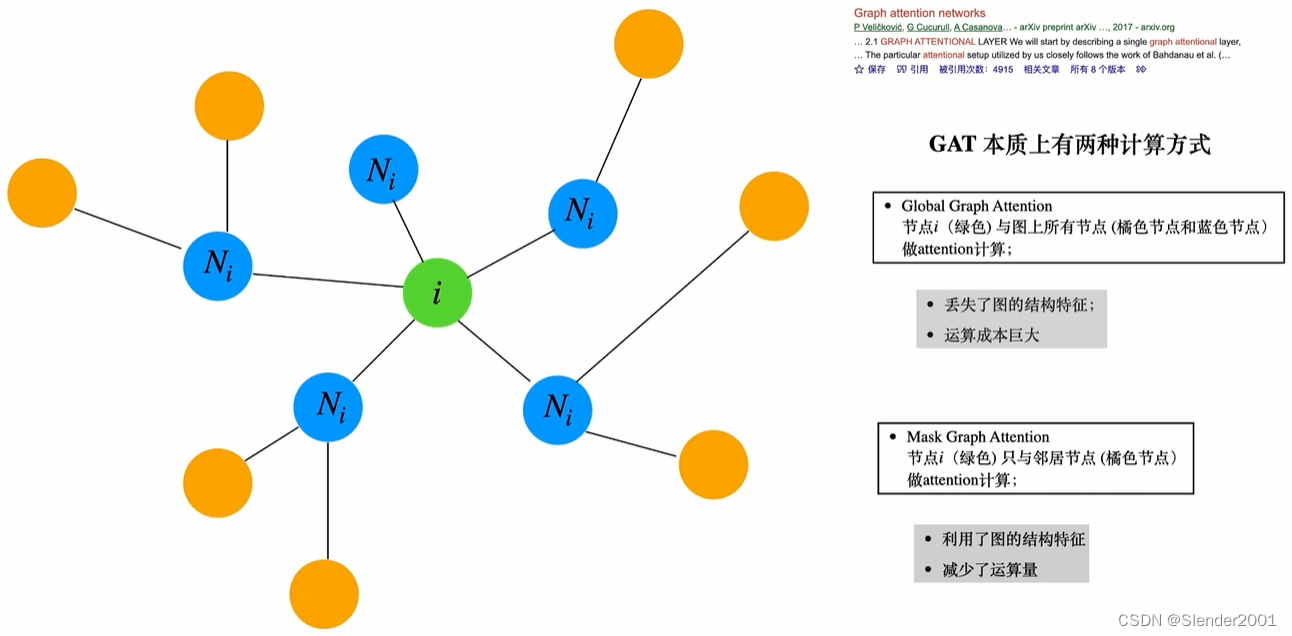
GAT（图注意力）的本质是让每一个节点和其他的节点计算Attention。Attention的方式有两种，一种是Global Graph Attention，即让当前节点和所有其他节点作Attention计算；另一种是Mask Graph Attention，即让当前节点只与邻居节点作Attention计算。Global Graph Attention的方式会缺失图的结构特征，因为在图结构数据中一个节点通常不会和其他所有节点都有边，如果计算与其他所有节点的Attention则会忽略掉这些节点是否与当前节点相邻这一信息，同时Global Graph Attention的计算量巨大。相反，Mask Graph Attention不会缺失图的结构特征，而且计算成本更小。

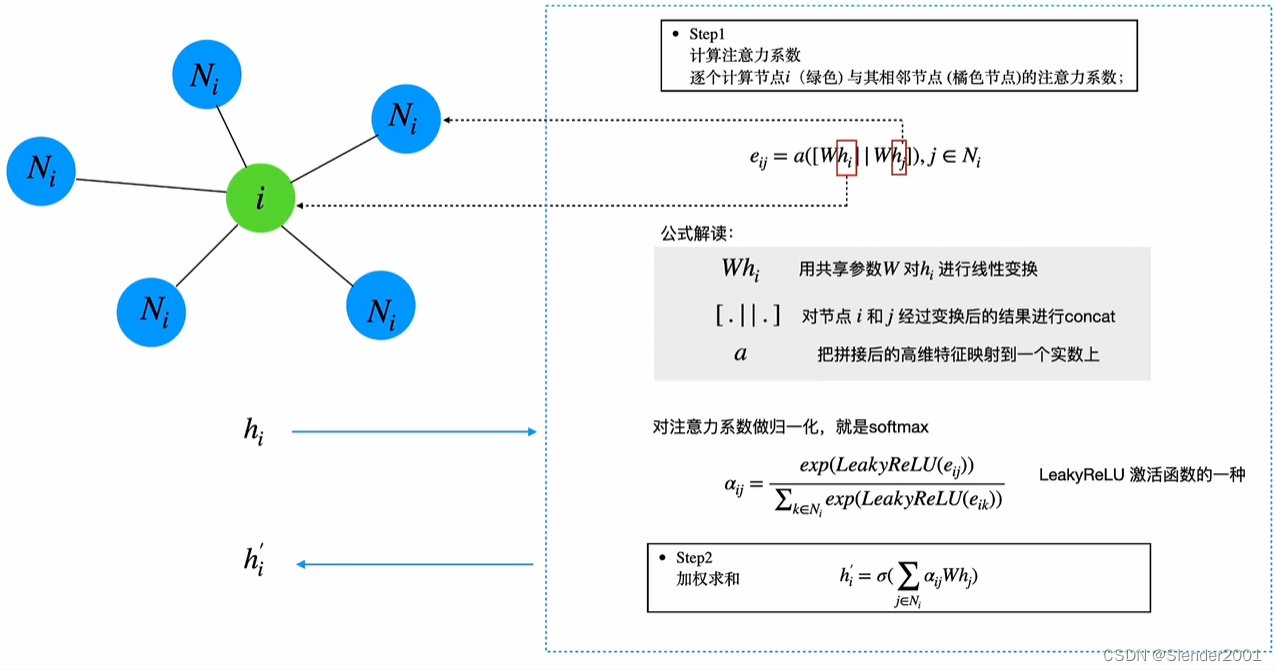
GAT的具体计算流程如下。第一步，逐点计算节点 $i$ 与其邻居节点 $N_{i}$ 之间的注意力系数，计算公式为 $e_{ij}=a([Wh_{i}||Wh_{j}]),j \in N_{i}$ ， $a_{ij}=\frac{exp(LeakyReLU(e_{ij}))}{\sum_{k\in N_{i}}^{} exp(LeakyReLU(e_{ik}))}$ 。其中 $W$ 为共享参数，对 $h_{i}$ 和 $h_{j}$ 作线性变换； $[\cdot || \cdot]$ 表示拼接操作； $a$ 将拼接后的高维特征映射到一个实数上； $a_{ij}$ 是使用softmax归一化后的注意力系数。第二步，加权求和，公式为 $h{}'_{i}=\sigma (\sum_{j\in N_{i}}^{} a_{ij}Wh_{j})$ ，至此节点更新完毕。

GAT代码如下：

import torch
import torch.nn as nn
import torch.nn.functional as Fclass GATLayer(nn.Module):def __init__(self, in_features, out_features, dropout, alpha, concat=True):super(GATLayer, self).__init__()self.in_features = in_features  # 定义节点向量的特征维度self.out_features = out_features  # 经过GAT之后的特征维度self.dropout = dropout  # dropout参数self.alpha = alpha  # LeakyReLU的参数# 定义可训练参数，即公式中的W和aself.W = nn.Parameter(torch.zeros(size=(in_features, out_features)))nn.init.xavier_uniform_(self.W.data, gain=1.414)  # xavier初始化self.a = nn.Parameter(torch.zeros(size=(2 * out_features, 1)))nn.init.xavier_uniform_(self.a.data, gain=1.414)  # xavier初始化# 定义LeakyReLUself.LeakyReLU = nn.LeakyReLU(self.alpha)def forward(self, input_h, adj):""":param input_h: [N, in_features]:param adj: 图的邻接矩阵，维度[N,N]:return: output_h"""h = torch.mm(input_h, self.W)  # [N, out_features]N = h.size()[0]  # 图的节点数input_concat = torch.cat([h.repeat(1, N).view(N * N, -1), h.repeat(N, 1)], dim=1).view(N, -1,2 * self.out_features)e = self.LeakyReLU(torch.matmul(input_concat, self.a).squeeze(2))zero_vec = -1e12 * torch.ones_like(e)attention = torch.where(adj > 0, e, zero_vec)attention = F.softmax(attention, dim=1)attention = F.dropout(attention, self.dropout, traning=self.training)output_h = torch.matmul(attention, h)return output_h

这篇关于机器学习周记（第三十三周：文献阅读[GWO-GART]）2024.4.1~2024.4.7的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！