【题解 | 分组背包】从栈中取出 K 个硬币的最大面值和

本文主要是介绍【题解 | 分组背包】从栈中取出 K 个硬币的最大面值和，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

从栈中取出 K 个硬币的最大面值和

力扣：2218. 从栈中取出 K 个硬币的最大面值和

一张桌子上总共有 n 个硬币栈。每个栈有 正整数 个带面值的硬币。

每一次操作中，你可以从任意一个栈的顶部取出 1 个硬币，从栈中移除它，并放入你的钱包里。

给你一个列表 piles ，其中 piles[i] 是一个整数数组，分别表示第 i 个栈里 从顶到底 的硬币面值。同时给你一个正整数 k ，请你返回在恰好进行 k 次操作的前提下，你钱包里硬币面值之和 最大为多少 。

示例 1：

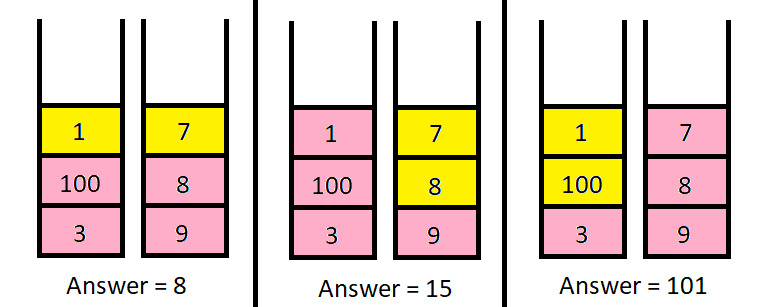
输入：piles = [[1,100,3],[7,8,9]], k = 2
输出：101
解释：
上图展示了几种选择 k 个硬币的不同方法。
我们可以得到的最大面值为 101 。

示例 2：

输入：piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
输出：706
解释：
如果我们所有硬币都从最后一个栈中取，可以得到最大面值和。

提示：

n == piles.length
1 <= n <= 1000
1 <= piles[i][j] <= 10^5
1 <= k <= sum(piles[i].length) <= 2000

解题思路

这道题很有意思，可以看作是分组背包问题。

在分组背包问题中，我们有多个组，每个组有多个物品，每组只能选一个物品，我们需要在总容量不超过背包容量的情况下，使得所选物品的总价值最大。

那这道题如何看作是分组背包问题？

实际上，每个硬币堆就是一个组，每组只能挑选一个物品（在这个问题中我们称之为方案，每个方案都是挑选前x个硬币），每个物品的体积就是所选方案的硬币数量（也可以理解为操作次数，因为一次操作获取一个硬币），那背包容量就是总操作次数（也就是一共可以拿多少枚硬币）。

算法步骤如下：

初始化动态规划表，dp[i][j] 表示前i组里面，每组挑选一个方案，在容量为j的情况下（j个硬币）获得的最大价值。
遍历每一组硬币堆，对于每一组，我们可以选择取出0到t个硬币，其中t是当前硬币堆的硬币数量和k中的较小值。
对于每一组，我们预处理前缀和，为了加速计算每个方案下前x个硬币的总价值（面值）。
更新动态规划表，对于每一组，我们可以选择取出0到t个硬币，对于每个可能的取出硬币的数量，我们更新dp[i][j]的值，使其为最大值。
最后，dp[n][k]就是我们的答案，即进行k次操作的前提下，钱包里硬币面值之和最大为多少。

参考代码如下：

class Solution {public int maxValueOfCoins(List<List<Integer>> piles, int k) {// 有 n 组硬币堆int n = piles.size();// dp[i][j] 表示前i组里面，每组挑选一个方案，在容量为j的情况下（j个硬币）获得的最大价值int[][] dp = new int[n + 1][k + 1];// 遍历每一组硬币堆for (int i = 1; i <= n; i++) {// 拿到第 i 组的硬币堆 groupList<Integer> group = piles.get(i - 1); // piles是从下标0开始的// 当前最多能取出 t 个硬币int t = Math.min(group.size(), k);// 预处理前缀和，为了加速计算每个方案下若干硬币的总价值（面值）int[] preSum = new int[t + 1];for (int j = 0, sum = 0; j < t; j++) {sum += group.get(j);preSum[j + 1] = sum;}// 更新动态规划表for (int j = 0; j <= k; j++) {// 当前方案取 0 个硬币dp[i][j] = dp[i - 1][j];// 当前方案取前 x 个硬币for (int x = 1; x <= Math.min(t, j); x++) {dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - x] + preSum[x]);}}}return dp[n][k];}
}

空间压缩版本：

class Solution {public int maxValueOfCoins(List<List<Integer>> piles, int k) {// 初始化动态规划数组，dp[j] 表示在容量为j的情况下（j个硬币）获得的最大价值int[] dp = new int[k + 1];// 遍历每一组硬币堆for (List<Integer> group : piles) {// 当前最多能取出 t 个硬币int t = Math.min(group.size(), k);// 预处理前缀和，为了加速计算每个方案下若干硬币的总价值（面值）int[] preSum = new int[t + 1];for (int j = 0, sum = 0; j < t; j++) {sum += group.get(j);preSum[j + 1] = sum;}// 从后向前更新动态规划数组，避免覆盖之前的数据for (int j = k; j > 0; j--) {// 当前组取 x 个硬币for (int x = 1; x <= Math.min(t, j); x++) {dp[j] = Math.max(dp[j], dp[j - x] + preSum[x]);}}}// 返回在恰好进行k次操作的前提下，你钱包里硬币面值之和最大为多少return dp[k];}
}