本文主要是介绍Deblo —— 树形DP+爆栈的解决方案,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Description

Input
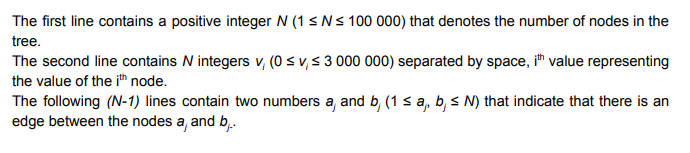
Output
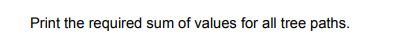
Sample Input
3
1 2 3
1 2
2 3
5
2 3 4 2 1
1 2
1 3
3 4
3 5
6
5 4 1 3 3 3
3 1
3 5
4 3
4 2
2 6
Sample Output
10
64
85
Hint

题意:
给你一棵树和每个点的权值,一条边的权值就是边上所有点的权值的异或,让你求出所有点的权值和+所有边的权值和
题解:
这道题可以用树形dp做,dp保存的是答案,num[i][j][k]保存的是在第i个点,第j位(0位就是1,1位就是2,2位就是4.。。。由于数的最大值只有3e6,那么我们可以保存每一位)的出现次数异或为k次(k是0或1,表示这位出现了奇数次或者偶数次)。那么状态转移方程就是dp[x]+=(1ll<<j)*num[ne][j][0]*num[x][j][1]+(1ll<<j)*num[ne][j][1]*num[x][j][0];然后在将儿子的状态保存到父亲这里,如果父亲在这一位是有的话,那么就是反一下:
num[x][j][0]+=num[ne][j][1],num[x][j][1]+=num[ne][j][0];
否则就是
num[x][j][0]+=num[ne][j][0],num[x][j][1]+=num[ne][j][1];
可能是我们学校oj过于垃圾,做这个用dfs的话会爆栈!!我wa了27发才过!爆栈的一种可能解决方法:用VC++交,加上下面的代码:
#pragma comment(linker,"/STACK:1024000000,1024000000")
但是!我们学校加上这个之后system error!在最后的时候才研究出来一种可以用栈来保存节点,找所有数的顺序,再放到队列里处理的方法
#include<stdio.h>#include<string.h>
#include<iostream>
#include<math.h>
#include<algorithm>
#include<queue>
#include<stack>
using namespace std;const int N=1e5+5;
#define ll __int64
ll dp[N],num[N][22][2];
struct node
{int to,next;
}e[N*2];
int cnt=1,head[N],a[N];
void add(int x,int y)
{e[cnt].to=y;e[cnt].next=head[x];head[x]=cnt++;
}
queue<int>Q;
int Fa[N];
bool vis[N];
int main()
{int i,j;int n,x,y;scanf("%d",&n);for(i=1;i<=n;i++){scanf("%d",&a[i]),dp[i]=a[i];for(j=0;j<=21;j++){if((a[i]&(1<<j)))num[i][j][1]=1;elsenum[i][j][0]=1;}}for(i=1;i<n;i++)scanf("%d%d",&x,&y),add(x,y),add(y,x);stack<int>S;S.push(1);vis[1]=1;while(!S.empty()){int p=S.top();int flag=0;for(i=head[p];i;i=e[i].next){int ne=e[i].to;if(vis[ne])continue;vis[ne]=1;S.push(ne);Fa[ne]=p;flag=1;}if(flag)continue;Q.push(p);S.pop();}ll ii=1;while(!Q.empty()){int x=Q.front();Q.pop();for(i=head[x];i;i=e[i].next){int ne=e[i].to;if(ne==Fa[x])continue;dp[x]+=dp[ne];for(j=0;j<=21;j++){dp[x]+=(ii<<j)*num[ne][j][0]*num[x][j][1]+(ii<<j)*num[ne][j][1]*num[x][j][0];if((a[x]&(1<<j)))num[x][j][0]+=num[ne][j][1],num[x][j][1]+=num[ne][j][0];elsenum[x][j][0]+=num[ne][j][0],num[x][j][1]+=num[ne][j][1];}}}printf("%I64d\n",dp[1]);return 0;
}这篇关于Deblo —— 树形DP+爆栈的解决方案的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







