本文主要是介绍Yalmip使用教程(7)-求解器的参数设置,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
博客中所有内容均来源于自己学习过程中积累的经验以及对yalmip官方文档的翻译:https://yalmip.github.io/tutorials/
这篇博客将详细介绍yalmip工具箱中常用的求解器设置选项。
1.求解器的基本设置
使用sdpsettings函数可以对求解的相关参数进行设置。最常用的设置选项包括求解器的选择(solver)、命令行结果展示的详细程度(verbose)与步骤展示(showprogress)。例如,下面的代码就是将求解器选择为cplex,结果展示的详细程度为0(最少的命令行展示,最大值为3),不显示步骤(showprogress为0):
ops = sdpsettings('solver','cplex','verbose',0,'showprogress',0);也可以先对选项结构体进行赋值,然后通过结构体操作修改具体选项的内容,例如:
ops = sdpsettings;
ops.solver = cplex;
ops.verbose = 0;
ops.showprogress = 0;Yalmip求解器的参数非常多,如果想要查看完整的参数,可以先定义一个默认的参数选项ops,然后在工作区或者命令行查看该结构体的内容:
>> opsops = 包含以下字段的 struct:solver: ''verbose: 1debug: 0usex0: 0warning: 1cachesolvers: 0showprogress: 0saveduals: 1removeequalities: 0savesolveroutput: 0savesolverinput: 0saveyalmipmodel: 0convertconvexquad: 1assertgpnonnegativity: 1thisisnotagp: 0radius: Infrelax: 0dualize: 0savedebug: 0expand: 1allowmilp: 1allownonconvex: 1shift: 0dimacs: 0beeponproblem: [-5 -4 -3 -2 -1]mosektaskfile: ''bisection: [1×1 struct]bilevel: [1×1 struct]bmibnb: [1×1 struct]bnb: [1×1 struct]cutsdp: [1×1 struct]kkt: [1×1 struct]moment: [1×1 struct]mp: [1×1 struct]mpcvx: [1×1 struct]plot: [1×1 struct]robust: [1×1 struct]sos: [1×1 struct]refiner: [1×1 struct]baron: []bintprog: [1×1 struct]bonmin: []cdcs: [1×1 struct]cdd: [1×1 struct]cbc: [1×1 struct]clp: [1×1 struct]cplex: [1×1 struct]coneprog: []csdp: [1×1 struct]dsdp: [1×1 struct]ecos: []filtersd: [1×1 struct]fmincon: [1×1 struct]fminsearch: [1×1 struct]frlib: [1×1 struct]glpk: [1×1 struct]gurobi: [1×1 struct]ipopt: [1×1 struct]intlinprog: [1×1 optim.options.Intlinprog]knitro: [1×1 struct]linprog: [1×1 struct]lmilab: [1×1 struct]lmirank: [1×1 struct]logdetppa: [1×1 struct]lpsolve: [1×1 struct]lsqnonneg: [1×1 struct]lsqlin: [1×1 struct]kypd: [1×1 struct]kktqp: [1×1 struct]nag: [1×1 struct]mosek: [1×1 struct]nomad: []ooqp: []penbmi: [1×1 struct]penlab: []pensdp: [1×1 struct]pop: [1×1 struct]qpoases: []osqp: []qsopt: [1×1 struct]quadprog: [1×1 struct]quadprogbb: [1×1 struct]scip: [1×1 struct]scs: [1×1 struct]sdpa: [1×1 struct]sdplr: [1×1 struct]sdpt3: [1×1 struct]sdpnal: [1×1 struct]sedumi: [1×1 struct]sparsepop: [1×1 struct]snopt: [1×1 struct]sparsecolo: [1×1 struct]vsdp: [1×1 struct]xpress: []default: [1×1 struct]2.常用参数详解
2.1 solver
参数solver表示yalmip在求解优化问题的将调用的求解器,如果没有指定solver参数,yalmip将自动选择已有合适的求解器,yalmip支持的求解器很多,支持的求解器和各个求解器的适用范围可参考官方文档的介绍:
Solvers - YALMIP
2.2 verbose
参数verbose表示yalmip在求解优化问题时候所展示的细节多少,取值为0时表示不展示求解的细节,取值为3时展示最多的求解细节。
2.3 debug
参数debug表示yalmip在求解过程中是否采用catch语句处理报错。如果debug参数设置为1,表示yalmip求解过程中报错时将直接显示在命令行(也就是我们在命令行常见的红色文字),如果将debug参数设置为0,yalmip求解过程中如果如果遇到错误将直接使用catch语句对错误进行处理。如果对catch语句用法不太清楚,可以尝试搜索matlab中try-catch语句的用法。
2.4 warning
参数warning表示yalmip是否在命令行显示警告,取1时表示显示警告,取0时表示不显示警告。
2.5 showprogress
参数showprogress表示是否展示Yalmip工具箱当前的动作,取1时将进行展示,取0时不展示。该参数和verbose参数类似,但有一定区别。verbose参数的取值表示时求解优化问题时候的细节,showprogress表示是否展示yalmip工具箱的动作,包括对约束条件进行处理,识别优化问题的类型等。
2.6 relax
参数relax表示对非线性约束的处理方式,如果relax设置为1,则将忽略所有非线性和完整性约束,整数变量被松弛为连续变量,非线性变量被视为独立的变量(例如x和x^2将被视为两个独立的变量)。如果设置为2,则仅松弛整数约束,如果设置为3,则仅松弛非线性约束。
2.7 usex0
参数usex0表示是否在求解优化问题时给定初值。如果将usex0参数设置为1,Yalmip会将变量的当前取值发送给求解器,作为求解时的初值。一般情况下,该参数可以和assign函数搭配使用。
在求解一些大规模优化问题时,如果已知优化问题的一组可行解,如果可以使用assign函数将这组可行解赋值给优化变量,并将usex0参数设为1,很可能将大大加快求解速度。
3.gurobi求解器的参数详解
从第一节所展示的ops所有参数可以看到,除了上述常用的参数选项之外,还有一些参数是结构体形式,点开后又有许多二级参数。其中最常用的就是求解器的参数,下面以常用的gurobi求解器为例进行讲解:
点开ops.gurobi,可以发现又有许多参数:
ops.gurobians = 包含以下字段的 struct:BarIterLimit: 1000BestBdStop: InfBestObjStop: -InfCutoff: InfIterationLimit: InfNodeLimit: InfSolutionLimit: InfTimeLimit: 7200BarConvTol: 1.0000e-08BarQCPConvTol: 1.0000e-06FeasibilityTol: 1.0000e-06IntFeasTol: 1.0000e-05MarkowitzTol: 0.0078MIPGap: 0.0100MIPGapAbs: 1.0000e-10OptimalityTol: 1.0000e-06PSDTol: 1.0000e-06InfUnbdInfo: 0NormAdjust: -1ObjScale: 0PerturbValue: 2.0000e-04Quad: -1ScaleFlag: -1Sifting: -1SiftMethod: -1SimplexPricing: -1BarCorrectors: -1BarHomogeneous: -1BarOrder: -1Crossover: -1CrossoverBasis: 0QCPDual: 0BranchDir: 0ConcurrentJobs: 0ConcurrentMIP: 1DegenMoves: -1Disconnected: -1DistributedMIPJobs: 0Heuristics: 0.0500ImproveStartGap: 0ImproveStartNodes: InfImproveStartTime: InfLazyConstraints: 0MinRelNodes: -1MIPFocus: 0MIQCPMethod: -1NodefileDir: ''NodefileStart: InfNodeMethod: -1NonConvex: -1PartitionPlace: 15PumpPasses: -1RINS: -1SolFiles: ''SolutionNumber: 0StartNodeLimit: -1StartNumber: 0SubMIPNodes: 500Symmetry: -1VarBranch: -1ZeroObjNodes: -1AggFill: -1Aggregate: 1DualReductions: 1PreCrush: 0PreDepRow: -1PreDual: -1PreMIQCPForm: -1PrePasses: -1PreQLinearize: -1Presolve: -1PreSOS1BigM: -1PreSOS2BigM: 0PreSparsify: -1TuneCriterion: -1TuneJobs: 0TuneOutput: 2TuneResults: -1TuneTimeLimit: -1TuneTrials: 3PoolGap: InfPoolSearchMode: 0PoolSolutions: 10BQPCuts: -1Cuts: -1CliqueCuts: -1CoverCuts: -1CutAggPasses: -1CutPasses: -1FlowCoverCuts: -1FlowPathCuts: -1GomoryPasses: -1GUBCoverCuts: -1ImpliedCuts: -1InfProofCuts: -1MIPSepCuts: -1MIRCuts: -1ModKCuts: -1NetworkCuts: -1ProjImpliedCuts: -1RelaxLiftCuts: -1RLTCuts: -1StrongCGCuts: -1SubMIPCuts: -1ZeroHalfCuts: -1WorkerPassword: ''WorkerPool: ''CloudAccessID: ''CloudHost: ''CloudSecretKey: ''CloudPool: ''ComputeServer: ''ServerPassword: ''ServerTimeout: 60CSPriority: 0CSQueueTimeout: -1CSRouter: ''CSGroup: ''CSTLSInsecure: 0CSIdleTimeout: -1JobID: ''CSAPIAccessID: ''CSAPISecret: ''CSAppName: ''CSAuthToken: ''CSBatchMode: 0CSClientLog: 0CSManager: ''TokenServer: ''TSPort: 41954DisplayInterval: 5FeasRelaxBigM: 1000000FuncPieceError: 1.0000e-03FuncPieceLength: 0.0100FuncPieceRatio: -1FuncPieces: 0FuncMaxVal: 1000000IgnoreNames: 0IISMethod: -1JSONSolDetail: 0LogFile: ''LogToConsole: 1Method: -1MultiObjMethod: -1MultiObjPre: -1NumericFocus: 0ObjNumber: 0OutputFlag: 1Record: 0ResultFile: ''ScenarioNumber: 0Seed: 0Threads: 0UpdateMode: 1NoRelHeurWork: 0NoRelHeurTime: 0下面将对gurobi中常用的参数选项进行讲解。
3.1 MIPGap
MIPGap参数是指gurobi求解器的偏差终止条件。当整数规划的偏差下降到设定值后,优化终止。Gurobi中该参数计算公式如下:
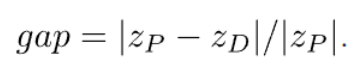
式中,ZP和ZD分别表示目标函数的上界和下界。当ZP=0且ZD≠0时,gap被视为无穷大。
该参数的默认值为 10^(-4),实际中如果对求解精度要求不是特别高,一般可以设定为 0.05 或者 0.01。修改该参数有两种方法,分别如下:
ops = sdpsettings('solver' , 'gurobi' , 'gurobi.MIPGap' , 0.01);或
ops = sdpsettings('solver' , 'gurobi' );
ops .gurobi.MIPGap = 0.01;第3节所有提到的参数修改都可采用相同的方式,后面不再赘述。
3.2 TimeLimit
TimeLimit参数表示gurobi求解器的时间终止条件。当达到规定的运行时间后,优化终止,该参数的单位为秒,默认值为inf(无穷大,即不限制求解时间)。但实际编程过程中,很多时候求解器会一直卡在某个进度,运行一天一夜也没有达到收敛,因此可以考虑对求解器的运行时间进行限制。
3.3 MIPFocus
MIPFocus参数表示MIP(混合整数规划)问题求解时所采取的策略,其默认值为0,试图在最优值和可行解之间取得平衡,取1时以可行解为优先目标,取2时以得到最优解为目标,取3时以优化边界为目标。
3.4 Presolve
Presolve参数表示gurobi求解优化问题时预优化的力度。其默认值为-1,表示,自动决定预优化力度。0:关闭预优化;1:保守;2:激进。
3.5 Method
Method参数表示gurobi求解优化问题时所采用的方法。其默认值为-1,自动决定优化方法。其他选项包括:0-原始单纯形,1-对偶单纯形,2-barrier,3-并发,4-确定性并发。
其中,并发方法不适用于QP和QCP。只有单纯形和barrier算法可用于连续QP模型。如果选择barrier算法来求解MIQP模型的根,则还需要为节点松弛选择barriel(即设置NodeMethod=2)。只有barrier算法可用于连续QCP模型。但是,如果选择LP松弛来求解MIQCP,也可以选择单纯形算法(方法=0或1)。
并发优化器在多个线程上同时运行多个解算器,并选择首先完成的解算器。并发运行的解算器可以使用ConcurrentMethod参数进行控制。确定性并发每次都会给出完全相同的结果,而非确定性并发(方式=3)通常更快,但在多次运行时可以产生不同的结果。
如果LP模型内存紧张,则应考虑使用对偶单纯形法。通常在使用默认设置时选择并发优化器,它比单独使用对偶单纯形消耗更多的内存。
3.6 ImproveStartTime和ImproveStartGap
ImproveStartTime和ImproveStartGap参数分别表示是否在一定时间或达到一定精度后改变gurobi的寻优策略,其中ImproveStartTime参数的单位为秒。ImproveStartTime和ImproveStartGap参数的默认值为inf和0,表示求解过程中不更改gurobi的寻优策略。如果将ImproveStartTime参数修改为10,表示gurobi求解器在运行10秒后将目标转为寻找可行解;同理,如果将ImproveStartGap参数修改为0.05,表示收敛精度达到0.05后将目标转为寻找可行解。
3.7 NoRelHeurTime和NoRelHeurWork
NoRelHeurTime和NoRelHeurWork参数分别表示gurobi在求解MIP问题时采用NoRel启发式算法的时间和工作量。其中NoRelHeurTime参数的单位为秒,NoRelHeurWork参数的单位为1。对于求解困难的混合整数规划问题,可以考虑使用这两个参数。两个参数主要的不同之处在于NoRelHeurTime所求结果具有不确定性,而NoRelHeurWork所得结果是具有确定性的。
3.6 Heuristics
Heuristics参数表示gurobi在求解优化问题时采用启发式算法的时间占比,其单位为1。默认值是0.05,表示gurobi求解过程中大约有5%的时间采用启发式方法。如果手中有一个很难找到初始可行解的混合整数规划问题,可以尝试增加Heuristics参数的取值。
3.7其他求解器参数设置
对于其他常用的cplex,mosek等求解器,也有许多参数选项,某些时候可以通过设置求解器参数提高求解效率,其中各自的参数选项均可从各自的使用手册上找到对应的含义和用法,此处不再赘述。
Cplex求解器参数选项文档:
List of CPLEX parameters - IBM Documentation
Mosek求解器参数选项文档:
15.5 Parameters (alphabetical list sorted by type) — MOSEK Optimizer API for C 10.1.28
这篇关于Yalmip使用教程(7)-求解器的参数设置的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





