本文主要是介绍机器学习工程师 |面试作业题记录|本科水平 | 附个人解答,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
如是我闻: 面试的是一家在加拿大的初创公司,我想他们是需要清纯质朴的廉价劳动力干点杂活,非常符合我目前的情况。祝我成功吧。以下是他们的面试作业题(take home questions),主要考察了一些基础知识,分享给各位同修做参考。
Question 1
1. Explain the principle of the gradient descent algorithm.
Answer

Question 2
2.Given the target function:
y ^ ( w 0 , w 1 ) = w 0 + w 1 x i \hat{y}(w_0,w_1)=w_0+w_1x_i y^(w0,w1)=w0+w1xi
And Error Function
E = ( y i − y ^ ( w 0 , w 1 ) ) 2 E = (y_i-\hat{y}(w_0,w_1))^2 E=(yi−y^(w0,w1))2
Assuming that a set of training examples N N N is provided, where each training example n ∈ N n\in N n∈N is associated with the target output y n y_n yn.
Find the cost function, J J J, and derive ∂ J ∂ w 0 \frac{\partial J}{\partial w_0} ∂w0∂J and ∂ J ∂ w 1 \frac{\partial J}{\partial w_1} ∂w1∂J
Answer
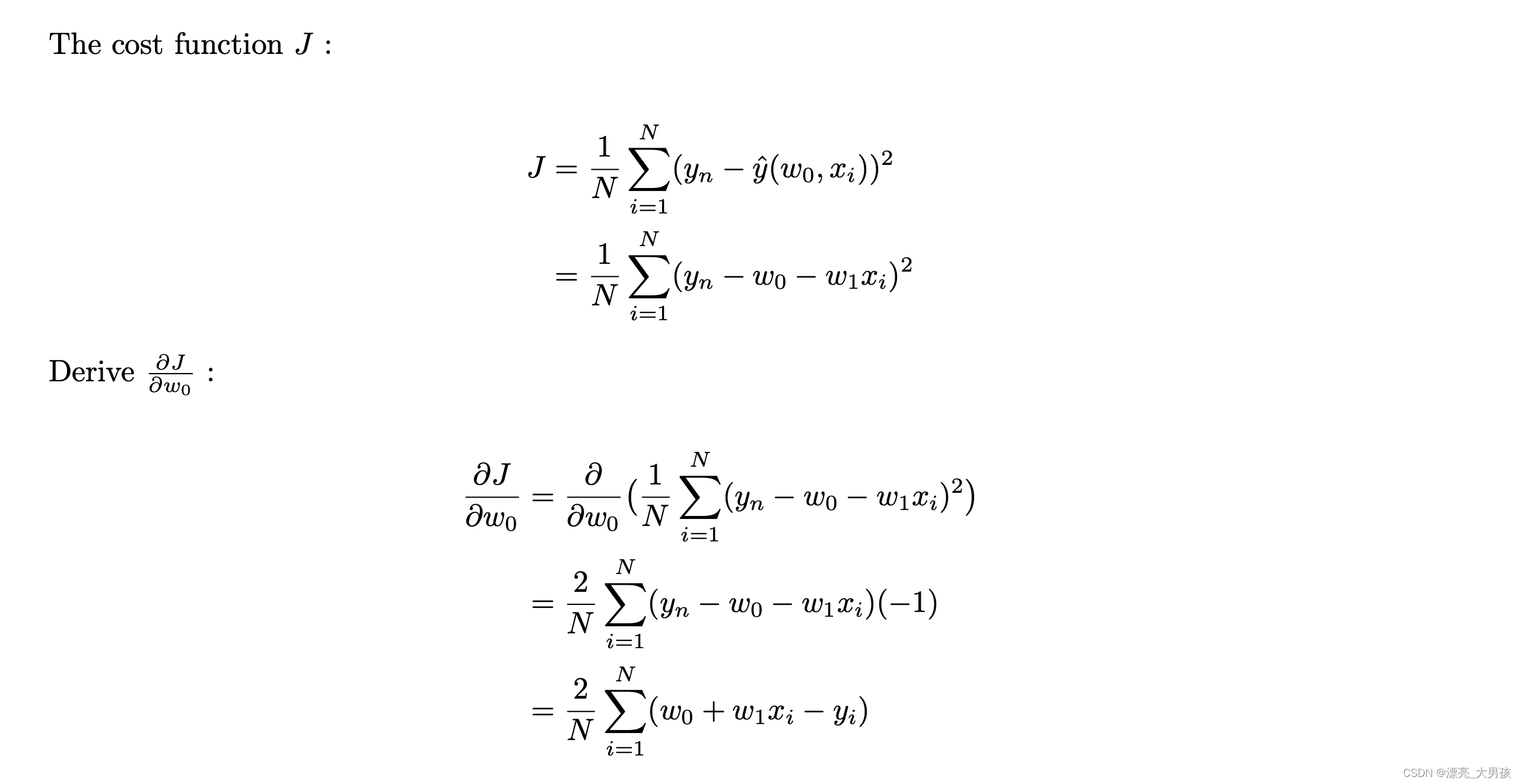
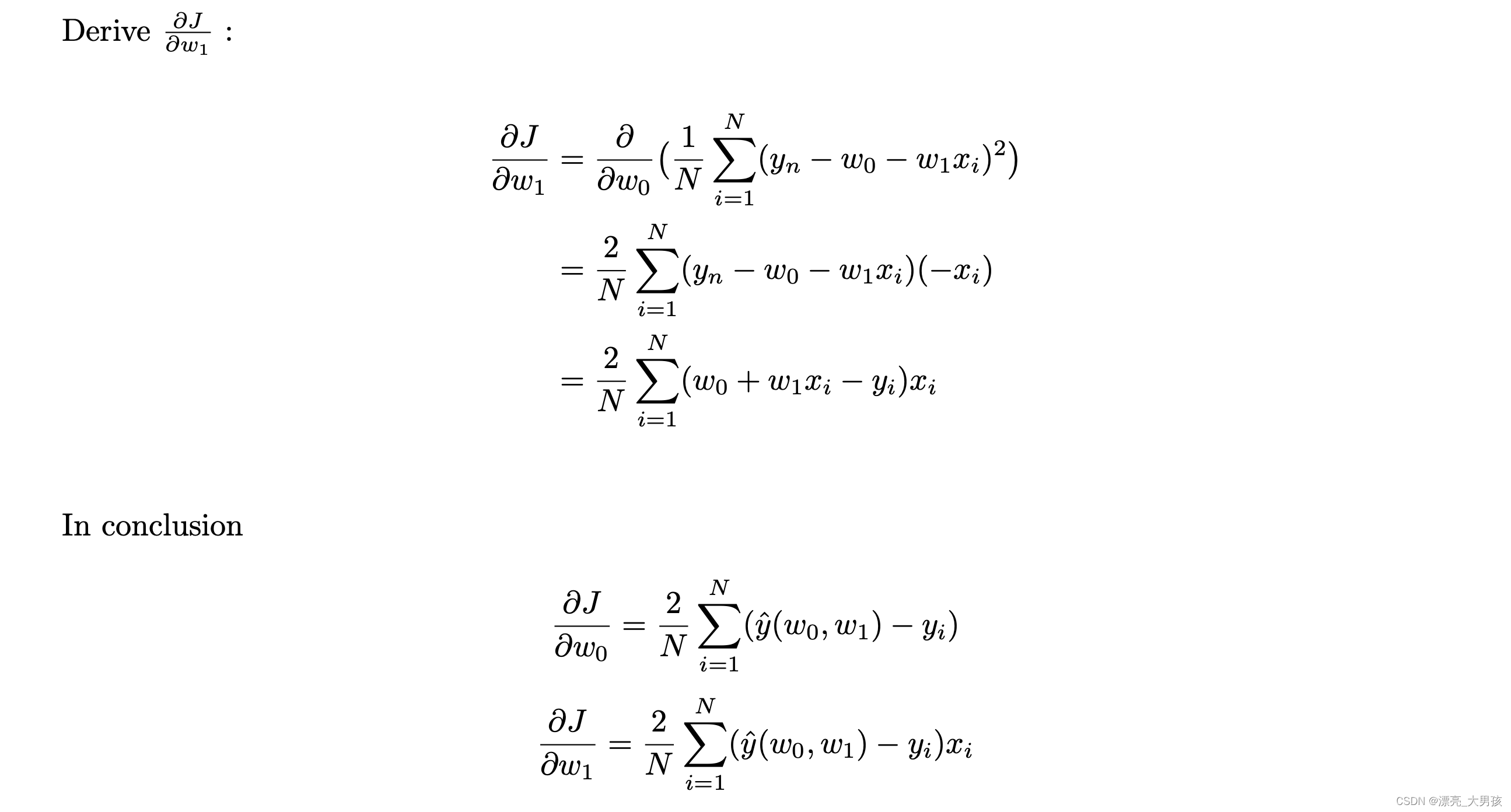
Question3
How would you design a Neural Network model to classify the diamonds from the crosses with as few as nodes and layers as possible.

Answer

Question4
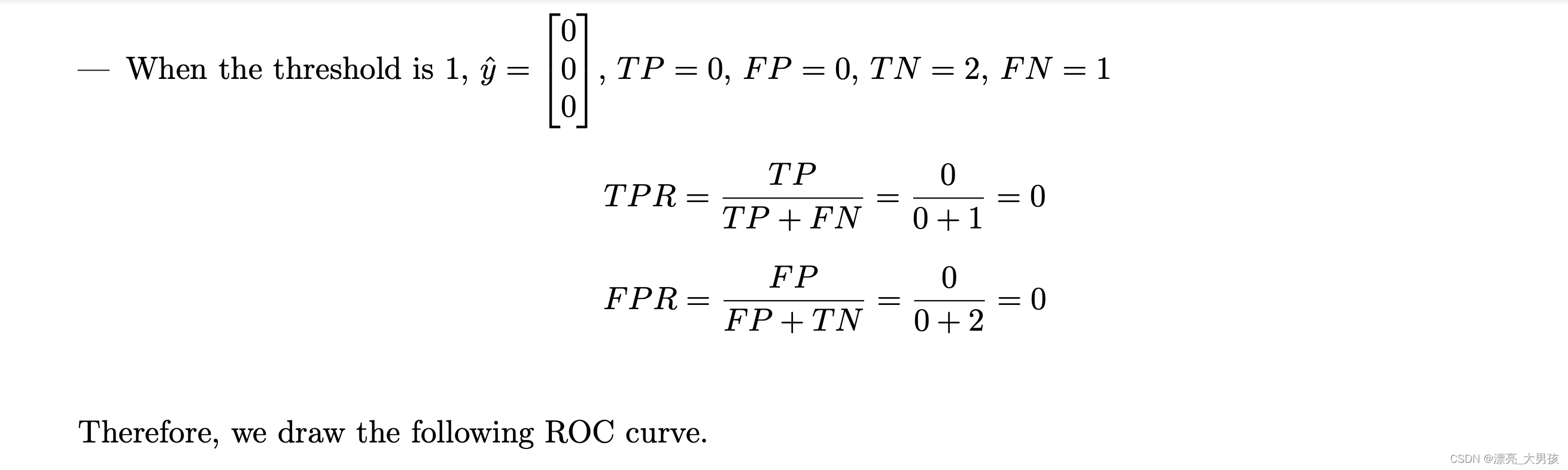
Given the simple logistic regression:
y ^ ( n ) = 1 1 + e x p ( − x ( n ) w ^ ) \hat{y}^{(n)}=\frac{1}{1+exp(-x^{(n)}\hat{w})} y^(n)=1+exp(−x(n)w^)1
Where: w ^ = − l o g 4 \hat{w}=-log4 w^=−log4
Given input features x = [ 1 0 1 ] x=\begin{bmatrix} 1\\ 0\\ 1\\ \end{bmatrix} x= 101 and Ground Truth y = [ 0 0 1 ] y=\begin{bmatrix} 0\\ 0\\ 1\\ \end{bmatrix} y= 001
Using thresholds t ∈ { 0 , 0.25 , 1 } t\in \{0,0.25,1\} t∈{0,0.25,1}, draw the ROC curve.
Answer

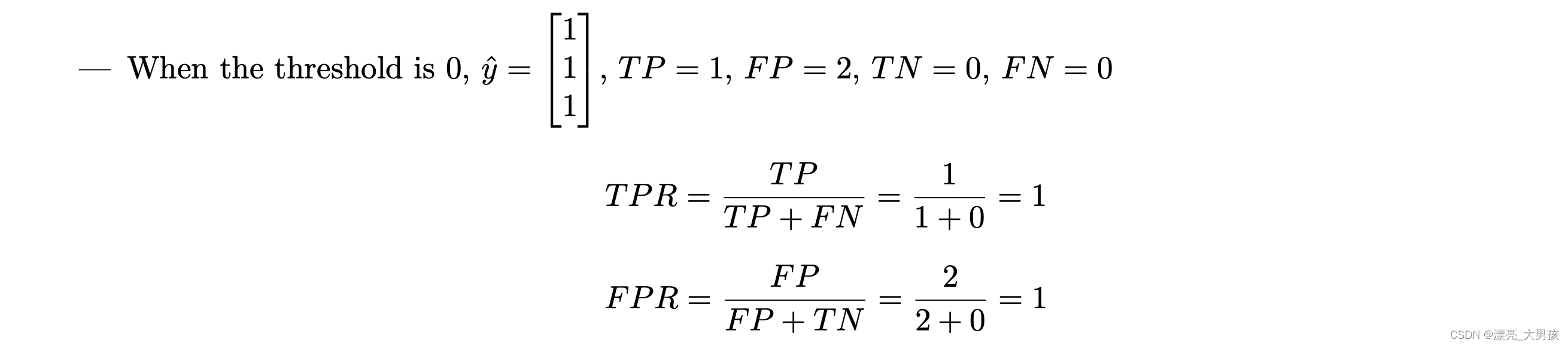
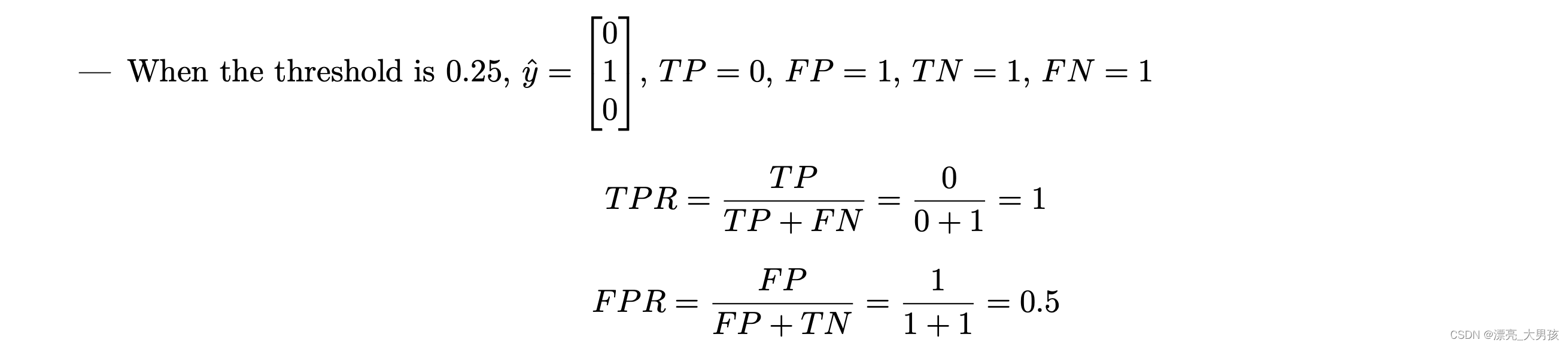
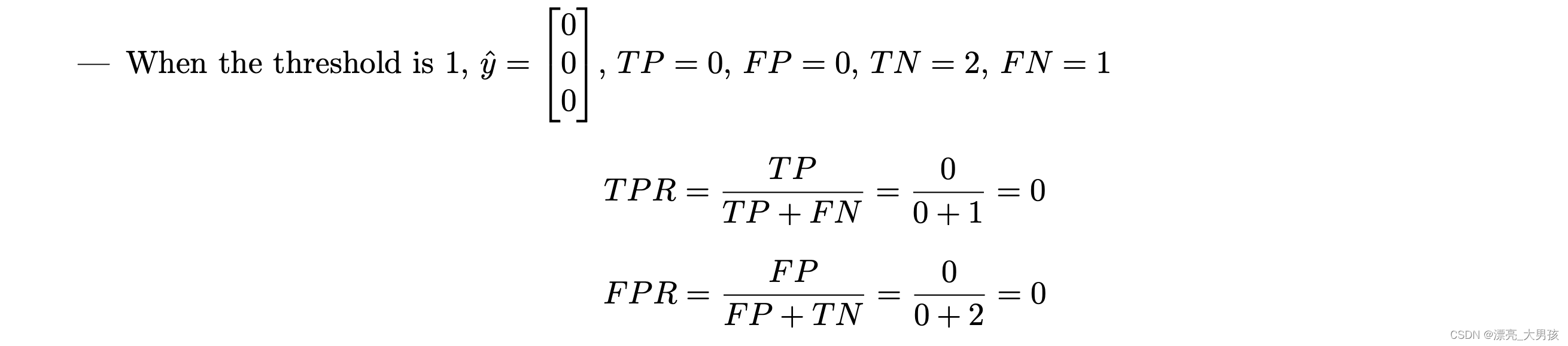

愿本文除一切找实习苦
非常的有品
以上
这篇关于机器学习工程师 |面试作业题记录|本科水平 | 附个人解答的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




