本文主要是介绍【PAT 1003】 Emergency 图论Dijkstra,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1003. Emergency (25)
As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.
Input
Each input file contains one test case. For each test case, the first line contains 4 positive integers: N (<= 500) - the number of cities (and the cities are numbered from 0 to N-1), M - the number of roads, C1 and C2 - the cities that you are currently in and that you must save, respectively. The next line contains N integers, where the i-th integer is the number of rescue teams in the i-th city. Then M lines follow, each describes a road with three integers c1, c2 and L, which are the pair of cities connected by a road and the length of that road, respectively. It is guaranteed that there exists at least one path from C1 to C2.
Output
For each test case, print in one line two numbers: the number of different shortest paths between C1 and C2, and the maximum amount of rescue teams you can possibly gather.
All the numbers in a line must be separated by exactly one space, and there is no extra space allowed at the end of a line.
5 6 0 2 1 2 1 5 3 0 1 1 0 2 2 0 3 1 1 2 1 2 4 1 3 4 1Sample Output
2 4
求单源点对最短路径数和最大的点权重之和。
分析:
求最短路径数用dijskra算法。关键是求相同最短路径的个数以及最大的点权重之和。
代码:
#include <iostream>
#include <fstream>
#include <algorithm>
#include <vector>
#include <cstring>using namespace std;//此代码使用前,需删除下面两行+后面的system("PAUSE")
ifstream fin("in.txt");
#define cin finconst int CITYNUM = 500;
const int INF = 0x7fffffff;int city[CITYNUM]; //记录各个城市的团队数
int road[CITYNUM][CITYNUM]={0};
bool visited[CITYNUM]={false};
int minLen[CITYNUM]={0}; //从源城市到达index城市的最短路径值
int sum[CITYNUM]={0}; //从源城市到达index城市,所能召集的最大团队数
int same[CITYNUM]={0}; //从源城市到达index城市,具有相同最短的路径个数void Dij(int source,int dest,int n){ //dijkstra算法int i,t,mm,next;int count = 0;int cur = source;sum[cur]=city[cur];while(count< n-1){visited[cur]=true;mm=INF;for(i=0;i<n;i++){if(visited[i])continue;if(road[cur][i]){t = minLen[cur] + road[cur][i];if(t < minLen[i] || minLen[i]==0){ //到达城市i,出现新的最短路径minLen[i]=t;same[i]=1; //重新计数sum[i]=sum[cur]+city[i];}else if(t == minLen[i]){ //到达城市i,出现相同的最短路径same[i]++;if(sum[cur]+city[i] > sum[i]) //记下团队数较大的值sum[i]=sum[cur]+city[i];}}if(minLen[i] < mm && minLen[i]!=0){mm = minLen[i];next = i;}}minLen[cur] = mm;if(next == dest)break;cur = next;count++;}return;
}int main()
{int n,m,sc,dc;cin>>n>>m>>sc>>dc;int i;for(i=0;i<n;i++)cin>>city[i];int c1,c2;for(i=0;i<m;i++){cin>>c1>>c2;cin>>road[c1][c2];road[c2][c1]=road[c1][c2];}if(sc==dc){ //若所在地就是目的地 则直接输出结果cout<<1<<' '<<city[sc]<<endl;return 0;}Dij(sc,dc,n);cout<<same[dc]<<' '<<sum[dc]<<endl;system("PAUSE");return 0;
}
测试点
| 测试点 | 结果 | 用时(ms) | 内存(kB) | 得分/满分 |
|---|---|---|---|---|
| 0 | 答案正确 | 0 | 580 | 10/10 |
| 1 | 答案正确 | 0 | 710 | 3/3 |
| 2 | 答案错误 | 0 | 580 | 0/3 |
| 3 | 答案错误 | 0 | 1510 | 0/3 |
| 4 | 答案错误 | 0 | 1510 | 0/3 |
| 5 | 答案正确 | 0 | 1510 | 3/3 |
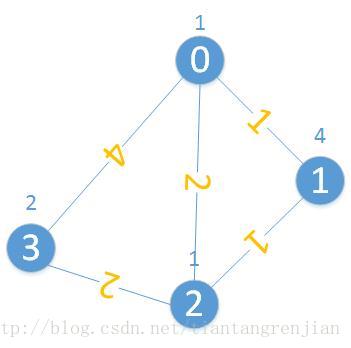
喔,经过和室友们的讨论,很快发现了问题所在。如下图这个Case:
输入数据为:
4 5 0 3
1 4 1 2
0 1 1
0 2 2
0 3 4
1 2 1
2 3 2
2号city的最短路径个数是2个,在计算目标3号city时需要考虑进去。
修改后,可AC的代码:
#include <iostream>
#include <fstream>
#include <algorithm>
#include <vector>
#include <cstring>using namespace std;//此代码使用前,需删除下面两行+后面的system("PAUSE")
ifstream fin("in.txt");
#define cin finconst int CITYNUM = 500;
const int INF = 0x7fffffff;int city[CITYNUM]; //记录各个城市的团队数
int road[CITYNUM][CITYNUM]={0};
bool visited[CITYNUM]={false};
int minLen[CITYNUM]={0}; //从源城市到达index城市的最短路径值
int sum[CITYNUM]={0}; //从源城市到达index城市,所能召集的最大团队数
int same[CITYNUM]={0}; //从源城市到达index城市,具有相同最短的路径个数void Dij(int source,int dest,int n){ //dijkstra算法int i,t,mm,next;int count = 0;int cur = source;sum[cur]=city[cur];same[cur]=1;while(count< n-1){visited[cur]=true;mm=INF;for(i=0;i<n;i++){if(visited[i])continue;if(road[cur][i]){t = minLen[cur] + road[cur][i];if(t < minLen[i] || minLen[i]==0){ //到达城市i,出现新的最短路径minLen[i]=t;same[i]=same[cur]; //重新计数,可能到达本节点cur的最短路径有多条sum[i]=sum[cur]+city[i];}else if(t == minLen[i]){ //到达城市i,出现相同的最短路径same[i]+=same[cur];if(sum[cur]+city[i] > sum[i]) //记下团队数较大的值sum[i]=sum[cur]+city[i];}}if(minLen[i] < mm && minLen[i]!=0){mm = minLen[i];next = i;}}minLen[cur] = mm;if(next == dest)break;cur = next;count++;}return;
}int main()
{int n,m,sc,dc;cin>>n>>m>>sc>>dc;int i;for(i=0;i<n;i++)cin>>city[i];int c1,c2;for(i=0;i<m;i++){cin>>c1>>c2;cin>>road[c1][c2];road[c2][c1]=road[c1][c2];}if(sc==dc){ //若所在地就是目的地 则直接输出结果cout<<1<<' '<<city[sc]<<endl;return 0;}Dij(sc,dc,n);cout<<same[dc]<<' '<<sum[dc]<<endl;system("PAUSE");return 0;
}
这篇关于【PAT 1003】 Emergency 图论Dijkstra的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!