一万小时定律的数学解释-可怕的复利

一、一万小时的来源

 

　　作家格拉德威尔在《异类》一书中指出：“人们眼中的天才之所以卓越非凡，并非天资超人一等，而是付出了持续不断的努力。1万小时的锤炼是任何人从平凡变成超凡的必要条件。“”他将此称为“一万小时定律”。要成为某个领域的专家，需要一万小时，按比例计算就是：如果每天工作八个小时，一周工作五天，那么成为一个领域的专家至少需要五年。这就是一万小时定律。

 　　 这里有一个典型的代表刘翔；田坛飞人刘翔，我们只看见他在赛场上的风驰电掣，一骑绝尘，可是为了他在赛场上的10多秒的辉煌，他从7岁开始至今已苦练了19年，不知跑了几个一万小时，汗水流了几吨，经历了多少挫折和失败，才换来了“阳光总在风雨后”。

   

二、一万小时对应时间表，一年按365天计算,倘若计划Y年完成，那么每天需要刻意练习H小时/M分钟；

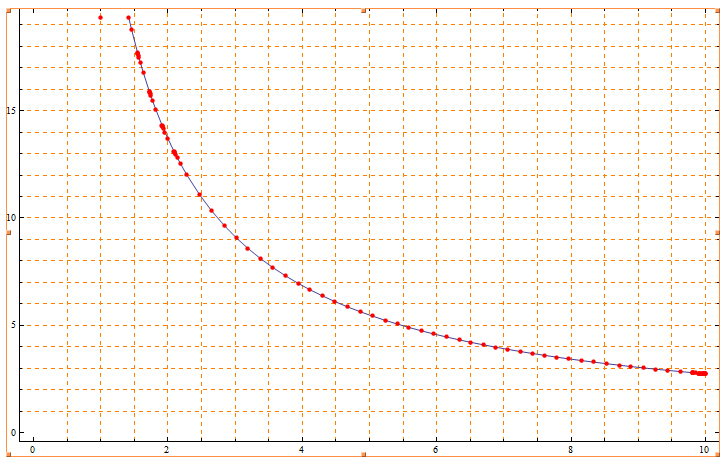
      若你打算1年就完成，这是不可能的，因为这样每天需要花费近乎27小时，然而大家都清楚一天你只有24小时；同理，2年也不太可能；你还要休息，吃饭，睡觉的时间；1万小时需要长期坚持，坚持，坚持......

     合理的选择是在3年以上根据自己情况合理选择训练的时间；

　　 当然每个人的情况都不一样，时间需要大家合理安排，没有唯一确定的方法。以我自己为例：首先认识到一万小时理论中提到的长期的刻意训练学习的确是有用的。其次考虑自己身体健康状况，年龄等因数的制约；最后我选择了7年的时间方案，每天坚持3小时55分钟，约4个小时。

 三、坚持与不坚持的差别

　　假设一个人A一天的时间价值为1，A每天坚持学习产生的价值为0.01（一天能够产生的价值非常的小）；则按复利计算，第x天的价值可以表述为f(x);

　　同理，假设一个人B一天的时间价值为1，B每天浪费一点时间损失的价值为0.01（一天损失的价值也是非常的小）；则按复利计算，第x天损失价值可以表述为g(x);

　　那么，第x天A、B之间的积累比可以用t(x)表述；

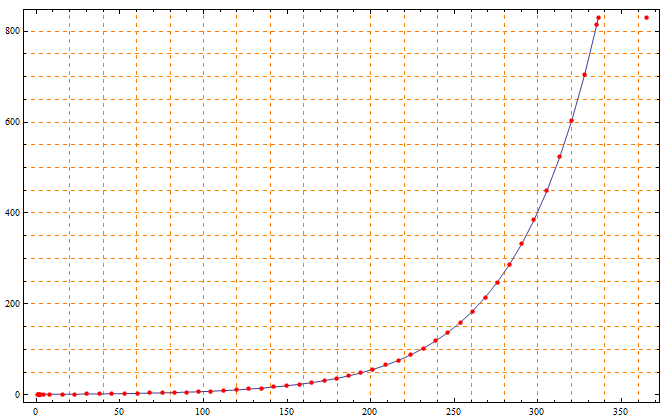
　　可以看出，至少前200天，也就是7个月前两者的差距都是非常的小的，但是如此下去到第10个月(300天)的时候，差距就非常的惊人了，约有400倍的差距；

　　如果你说1年的时间看不出差别，那我们把时间的尺度放大到10年，可以看出，至少前2800天，也就是约7.7年前两者的差距都是非常的小的，但是如此下去到第8.2年(3000天)的时候，差距就非常、非常、非常的惊人了；量变引起质变，没有量的积累，一切都是空想！

　　当然，这里的模型是非常极端的情况，所以越是到最后，差距非常的大。现实的情况很可能A并不是每天都能够积累0.01,很可能"三天打鱼，两天晒网"。B也并非无药可救，每天都会损失0.01;很可能发现问题不对劲后会迎头赶上。这里只是在非常极端的情况下的一种趋势推测，现实情况远远比这复杂的多。

　　写到此时，我有一种醍醐灌顶的感觉，忽然脑海中涌出荀子的名言：

    “不积跬步，无以至千里；

   不积小流，无以成江海。

   骐骥一跃，不能十步，

   驽马十驾，功在不舍。

   锲而舍之，朽木不折；

   锲而不舍，金石可镂。”

 

谨以此句自励，自警，自醒。