本文主要是介绍Python环境下基于离散小波变换的信号降噪方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Mallat创造了小波分析中的经典理论之一,即多分辨率分析的概念。后来,在Mallat与Meyer的共同努力之下,他们又在这一理论的基础上发明了离散小波变换的快速算法,这就是Mallat塔式算法,这种算法可以大量减少计算时间。在之前的二十年之间,小波分析方法在自身不断发展壮大的同时,也被许多学者在信号降噪领域进行了普及与应用。以Mallat为代表的一系列学者提出了模极大值重构滤波方法。这一方法的原理是:信号与噪声的小波系数在变换尺度变化的情况下,Lipschitz指数会呈现出不同的变化特点,以此来分辨信号与噪声从而进行滤波处理。
Donoho和JollllStone等在小波变换的基础上首次提出了小波域阈值滤波原理,该原理认为幅值较大的小波系数是由信号产生的。随后Donoho进一步完善了该方法,并在高斯噪声模型下推导出了通用阈值公式。Coifman和Donoho在进一步完善了小波阈值滤波方法后,提出了一种既能有效地实现信号降噪,又能抑制伪吉布斯现象的方法,这就是平移不变量降噪法。
在综上所述的所有方法中,小波域阈值降噪方法在实际操作上更为简便,同时在计算上的工作量相比于其他方法也少很多,因而得到了最为广泛的应用。这也是本文选取小波阈值降噪方法开展试验探索的原因之一。但是,如何选择小波基与阈值函数,以及怎样来确定阈值等等,这些都是小波阈值降噪方法在实践中亟待解决的几个关键问题。常用的小波基种类有很多,所以对于不同的信号,选择什么样的小波函数能实现最优的降噪效果是一个有待解决的问题。
对于如何选取阈值函数的问题,可以从显示和隐式两类阈值函数分别进行分析。首先显式阈值函数秉持的核心观点是:仅处理较大的小波系数,而将较小的统统去掉。具体的代表有:硬阈值和软阈值两种阈值函数,对于数值较大的小波系数,硬阈值函数对其进行了保留,而软阈值函数却对其进行了一定的收缩处理;
基于Donoho的研究成果,有学者提出了半软阈值函数,但是在实际的操作中,需要确定两个阈值以及计算上的复杂性成为它在实践中的缺点;为了弥补这一系列不足,有学者又在不久之后提出用Garrote函数作为阈值函数,这样做的原因在于这种阈值函数在形式上类似于硬阈值函数,其自身具有一定程度的连续性。其次,隐式阈值函数是以贝叶斯模型为基础提出来的,它围绕的核心思想是假设真实信号的小波系数服从某一先验分布。这类阈值函数的确定往往需要扎实的统计学基础,且操作起来难度较大,在实际应用中并不多见,缺少一定的实践意义,此处便不再赘述。
对于降噪方法,还有一个问题不容忽视,即如何选择阈值。Donoho首先提出了通用阈值,之后,其在对于SURE函数的研究中,提出了Stein无偏风险阈值。Jason将广义交互验证原理用于降噪算法,可在不知道噪声方差的情况下获得最优的阈值。Abramovich把小波阈值处理当作一种多重假设检验问题,并使用错误发现率方法去检验它以获取最优阈值,该阈值称为FDR阈值。Chang基于贝叶斯框架,认为小波系数服从广义高斯分布,提出了一种简单且封闭式的阈值——贝叶斯阈值,该阈值在图像处理领域得到了广泛应用。
该项目采用简单的离散小波分解对信号进行降噪,采用多种阈值方法,如下:
1. **universal**
The threshold, in this case, is given by the formula MAD x sqrt{2 x log(m)},
where MAD is the Median Absolute Deviation, and m is the length of the signal.
2. **sqtwolog**
Same as the universal, except that it does not use the MAD.
3. **energy**
In this case, the thresholding algorithm estimates the energy levels
of the detail coefficients and uses them to estimate the optimal threshold.
4. **stein**
This method implements Stein's unbiased risk estimator.
5. **heurstein**
This is a heuristic implementation of Stein's unbiased risk estimator.
运行环境为Python环境,所使用的模块如下:
numpy
scipy
matplotlib
scikit-learn
PyWavelets
Pandas运行代码如下:
import numpy as np
# import pandas as pd
import matplotlib.pylab as plt# from scipy.signal import butter, filtfilt
from scipy.signal import spectrogramfrom denoising import WaveletDenoisingdef plot_coeffs_distribution(coeffs):"""! Plots all the wavelet decomposition's coefficients. """fig = plt.figure()size_ = int(len(coeffs) // 2) + 1if size_ % 2 != 0:size_ = size_+1for i in range(len(coeffs)):ax = fig.add_subplot(size_, 2, i+1)ax.hist(coeffs[i], bins=50)def pretty_plot(data, titles, palet, fs=1, length=100, nperseg=256):"""! Plots the contents of the list data. """fig = plt.figure(figsize=(13, 13))fig.subplots_adjust(hspace=0.5, wspace=0.5)index = 1for i, d in enumerate(data):ax = fig.add_subplot(8, 2, index)ax.plot(d[:length], color=palet[i])ax.set_title(titles[i])ax = fig.add_subplot(8, 2, index+1)f, t, Sxx = spectrogram(d, fs=fs, nperseg=nperseg)ax.pcolormesh(t, f, Sxx, shading='auto')index += 2def run_experiment(data, level=2, fs=1, nperseg=256, length=100):"""! Run the wavelet denoising over the input data for each thresholdmethod."""# Experiments titles / thresholding methodstitles = ['Original data','Universal Method','SURE Method','Energy Method','SQTWOLOG Method','Heursure Method']# Theshold methodsexperiment = ['universal','stein','energy','sqtwolog','heurstein']# WaveletDenoising class instancewd = WaveletDenoising(normalize=False,wavelet='db3',level=level,thr_mode='soft',selected_level=level,method="universal",energy_perc=0.90)# Run all the experiments, first element in res is the original datares = [data]for i, e in enumerate(experiment):wd.method = experiment[i]res.append(wd.fit(data))# Plot all the results for comparisonpalet = ['r', 'b', 'k', 'm', 'c', 'orange', 'g', 'y']pretty_plot(res,titles,palet,fs=fs,length=length,nperseg=nperseg)if __name__ == '__main__':# ECG Dataimport pandas as pdfs = 100raw_data = pd.read_pickle("data/apnea_ecg.pkl")N = int(len(raw_data) // 1000)data = raw_data[:N].valuesdata = data[:, 0]run_experiment(data, level=3, fs=fs)plt.show()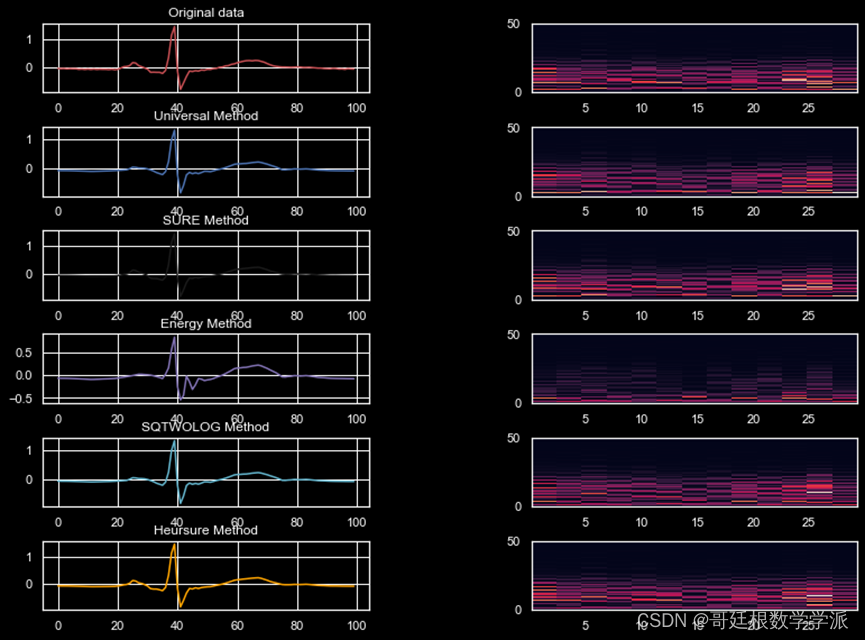
if __name__ == '__main__':raw_data = np.genfromtxt("./data/Z001.txt")fc = 40fs = 173.61w = fc / (fs / 2)b, a = butter(5, w, 'low')data = filtfilt(b, a, raw_data)run_experiment(data, level=4, fs=fs)plt.show()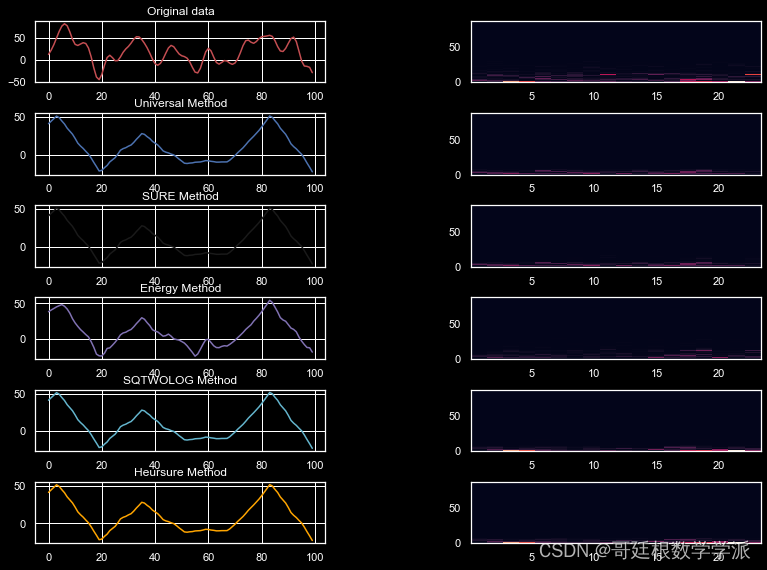
完整代码:Python环境下基于离散小波变换的信号降噪方法
工学博士,担任《Mechanical System and Signal Processing》等期刊审稿专家,擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。
这篇关于Python环境下基于离散小波变换的信号降噪方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



