本文主要是介绍不堪大用的pow，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
【题目描述】
输出100～999中的所有水仙花数。若3位数ABC满足
，则称其为水仙花
数。例如
，所以153是水仙花数。
【题目来源】
刘汝佳《算法竞赛入门经典 第2版》习题2-1 水仙花数（daffodil）
题目很简单，利用分离整数的方法将数字分离后判断是否满足水仙花数条件即可，代码如下：
#include<stdio.h>
int main(){for(int i=100; i<=999; i++){int ge = i%10;int shi = i/10%10;int bai = i/100;if(i == bai*bai*bai + shi*shi*shi + ge*ge*ge){printf("%d\n", i);}}return 0;
}为什么这样的数会叫“水仙花数”呢？
它源于一个古老的传说。说有一位名叫纳西塞斯的年轻人，他过于自恋，看到水中自己的影子不能自已，于是纵身一扑……
在他死去的地方，长出了一株水仙花。
人们为了纪念这位自恋的年轻人，将这种同样有自恋特质的数命名为“水仙花数”。
如果把水仙花数的公式写成下面这种形式，你就能充分品味出它的自恋特质了。
ABC = A*A*A + B*B*B + C*C*C
不过，这里老金想提的是另一个问题：假设用pow()函数求立方有没有问题？
本题老金测试过是完全没有问题的。但网上普遍说pow()因为浮点数的原因是存在误差的，即便底数和指数都是整数。
老金不知道pow()的内部实现是什么样的（据说算法非常复杂），但老金知道，整数值是不会产生浮点数误差的，导致出现误差的是小数部分（详见《浮点数产生误差的根源》一文），所以老金认为，当底数和指数都是整数时，按理pow()函数也是不应该产生误差的。
实践是检验真理的唯一标准，编段代码测试一下：
#include<stdio.h>
#include<math.h>
int main(){long long a, b; //x的y次幂：a用循环求，b用pow求int cnt=0, cnt_dif=0; //记录计算次数、差异次数for(int x=1; x<=100; x++){for(int y=1; y<=9; y++){b = pow(x,y);a=1;for(int z=1; z<=y; z++){a *= x;}if(a != b){printf("%d %d %lld %lld\n", x, y, a, b);cnt_dif++;}cnt++;}}printf("%d %d", cnt, cnt_dif);return 0;
}思路很简单，分别用循环的方式和pow函数求出x的y次幂，对比二者的值是否一致，不一致就打印出来。
输出结果：
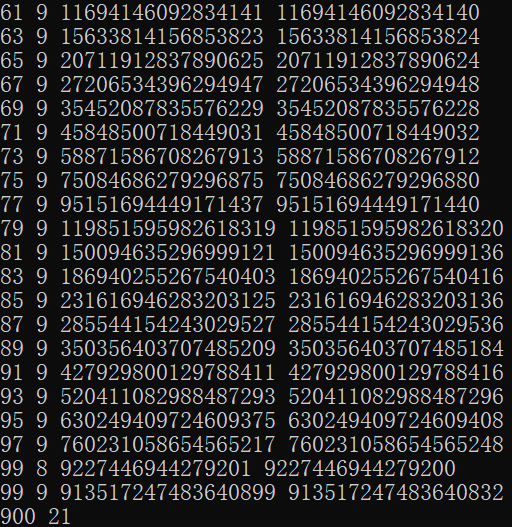
pow函数实在是不争气，辜负了老金的期望，900次运算中竟有21次产生了误差。
大哥，就是有一次也不行啊！
从上面的运行结果可以看出，产生误差的数都是非常大的幂（106
以上）。此外，指数基本都是9，只有一个是8，说明指数越大，越容易产生误差。
不管怎么样，这个结果都证明了即便底数和指数都是整数，当幂的值变得足够大时，就会产生误差。
综上，避免用pow还是对的。
这篇关于不堪大用的pow的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
