【C++进阶】红黑树的复仇（红与黑的爱恨厮杀）

本文主要是介绍【C++进阶】红黑树的复仇（红与黑的爱恨厮杀），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

🪐🪐🪐欢迎来到程序员餐厅💫💫💫

          主厨：邪王真眼

主厨的主页：Chef‘s blog  

 所属专栏：c++大冒险
 

 总有光环在陨落，总有新星在闪烁

引言：

ps：建议先看过AVL树后再来学习红黑树：

带你手撕AVL树 

一. 红黑树的概念

推导：

• 性质1不必多说
• 性质2与后面的旋转有关
• 性质3表明不能有连续的红色结点
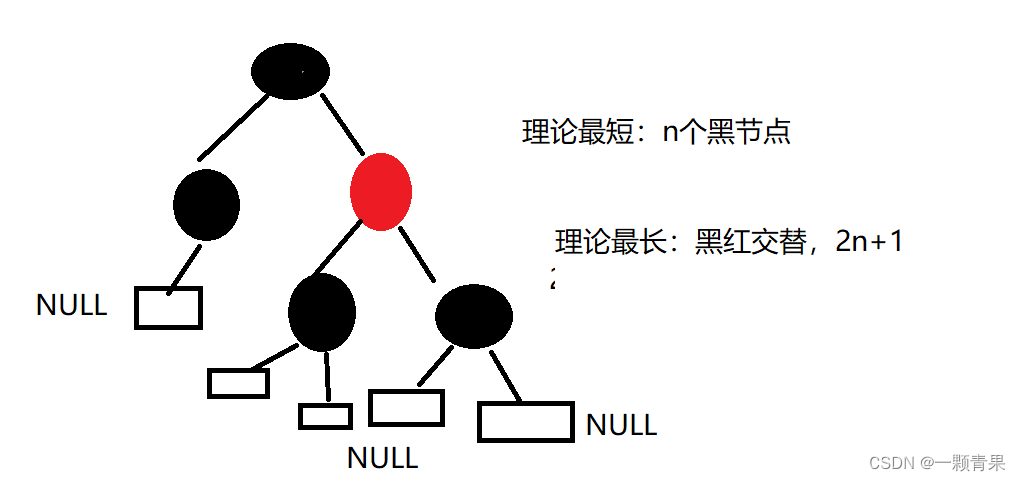
• 性质4表明理论最短路径就是纯黑节点路径

综上：

            我们可以认为事先建造好一颗纯黑节点的满二叉树，再在两个黑节点之间插入红节点，则理论最长路径就是一黑一红交替，不超过最短路径的二倍。

 三.红黑树的节点讲解及模拟

enum Color
{RED,BLACK
};
template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Color _col;RBTreeNode(pair<K, V>& kv = pair<K, V>()):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED)
};

代码讲解：

• 1.我们枚举出了Color
• 2.除左右指针外，还有父亲指针，使得可以向上回溯
• 3.用pair对象存储K值V值
• 4.增加了颜色的成员变量，且默认颜色为红色

提问：

           为什么结点的颜色初始化为红色呢？

回答：

           因为插入新节点时（不为根部），如果插入黑色，一定破坏性质4，导致每条路径黑结点数目不同；而如果插入红色，有可能不会破坏性质3，所以结点初始化为红色。

四.红黑树模拟

4.1 成员变量

template<class K, class V>
class RBTree
{
protected:typedef RBTreeNode<K, V> Node;
public://函数
protected :Node* _root;
};

4.2插入

与搜索二叉树以及AVL树相比，红黑树的默认成员函数和遍历相差不大，所以这里重点讲插入

4.2.1插入过程：

1. 以普通二叉搜索树的方式进行插入
2. 根据插入后的不同情况进行调整 

	bool Insert(pair<K, V>& kv){if (_root == nullptr){_root = new Node(val);return true;}else{Node* cur = _root;Node* parent = nullptrwhile (cur){parent = cur;if (cur->_val > val)cur = cur->left;else if (cur->_val < val)cur = cur->_right;elsereturn false;}cur = new Node(val);if (parent->_val.first > cur->_val.first){parent->_left = cur;}else{parent->_parent = cur;}cur->_parent = parent;///从此处开始进行插入后的调整while (parent && parent->_col == RED){Node* grandparent = parent->_parent;Node* uncle = nullptr;if (grandparent->_left == parent)uncle = grandparent->_right;elseuncle = grandparent->_left;if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;parent = cur->_parent;}else if (grandparent->_left == parent){if (parent->_left = cur){RotateR(grandparent);grandparent->_col = RED;parent->_col = BLACK;}else{RotateL(parent);RotateR(grandparent);grandparent->_col = RED;cur->_col = BLACK;}}else{if (parent->_right = cur){RotateL(grandparent);grandparent->_col = RED;parent->_col = BLACK;}else{RotateR(parent);RotateL(grandparent);grandparent->_col = RED;cur->_col = BLACK;}}void RotateL(AVLNode * parent)//左旋{Node* grandparent = parent->_parent;Node* ChildR = parent->_right;if (grandparent){if (grandparent->_left == parent)grandparent->_left = ChildR;elsegrandparent->_right = ChildR;}else_root = ChildR;ChildR->_parent = grandparent;parent->_right = ChildR->_left;ChildR->_left->_parent = parent;ChildR->_left = parent;parent->_parent = ChildR;ChildR->_bf = parent->_bf = 0;}void RotateR(AVLNode * parent)//右旋{Node* grandparent = parent->_parent;Node* ChildL = parent->_left;if (grandparent){if (grandparent->_left == parent)grandparent->_left = ChildL;elsegrandparent->_right = ChildL;}else_root = ChildL;ChildL->_parent = grandparent;//两两一组进行改变parent->_left = ChildL->_right;ChildL->_right->_parent = parent;ChildL->_right = parent;parent->_parent = ChildL;//ChildL->_bf = parent->_bf = 0;}void RotateRL(AVLNode * parent)//双旋，先右旋在左旋{Node* ChildR = parent->_right;int bf = ChildR->_left->_bf;RotateR(ChildR);RotateL(parent);if (bf == 0){parent->_bf = 0;ChildR->_bf = 0;ChildR->_left->_bf = 0;}else if (bf == 1){parent->_bf = -1;ChildR->_bf = 0;ChildR->_left->_bf = 0;}else if (bf == -1){parent->_bf = 0;ChildR->_left->_bf = 0;ChildR->_bf = 1;}else{assert(false);}}void RotateLR(AVLNode * parent)//双旋，先左旋，再右旋{Node* ChildL = parent->_left;int bf = ChildL->_right->_bf;RotateR(ChildL);RotateL(parent);if (bf == 0){parent->_bf = 0;ChildL->_bf = 0;ChildL->_right->_bf = 0;}else if (bf == 1){parent->_bf = 0;ChildL->_bf = -1;ChildL->_right->_bf = 0;}else if (bf == -1){parent->_bf = 1;ChildL->_right->_bf = 0;ChildL->_bf = 0;}else{assert(false);}}void Inorde(AVLNode * root, vector<pair<K, V>>&v){if (root == nullptr)return;Inorde(root->_left, v);v.push_back(root->_val);Inorde(root->_right, v);}}}}

插入后调整的分析：

• 1.像AVL树一样，大框架也是向上回溯，判断循环进行条件是父亲节点不为空且父亲节点颜色为红，.因为新节点的默认颜色是红色，如果其双亲节点的颜色是黑色，没有违反红黑树任何 性质，则不需要调整；
• 2当新插入节点的双亲节点颜色为红色时，就违反了性质三不能有连在一起的红色节点，此时需要对红黑树分情况来讨论：cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点

  ---

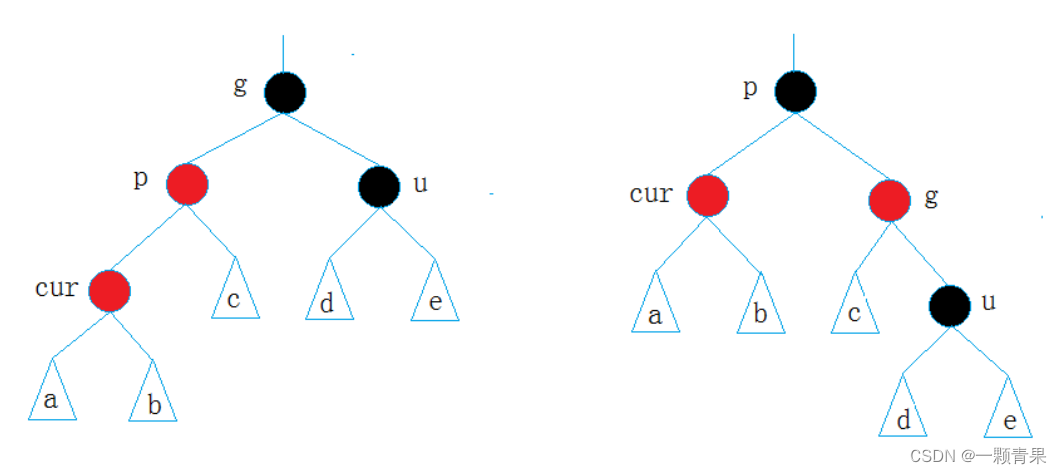
  🍒🍒4.2.2情况一：

cur为红，p为红，g为黑，u存在且为红 

cur为红，p为红，g为黑，u不存在/u存在且为黑，p是g的左孩子，cur是p的左孩子

解决方案：

1. 先对grandparent进行右单旋
2. 再将parent变黑，grandparent变红

🍒🍒4.2.4情况三

cur为红，p为红，g为黑，u不存在/u存在且为黑，p是g的左孩子，cur是p的右孩子

  重点提醒：

               可以发现左单旋后就变成了情况二

解决方案：

1. 先对parent进行左单旋
2. 再对grandparent进行右单旋
3. 最后将cur变黑，grandparent变红，这里将cur变黑而不是parent是因为左单旋后cur取代了parent的位置

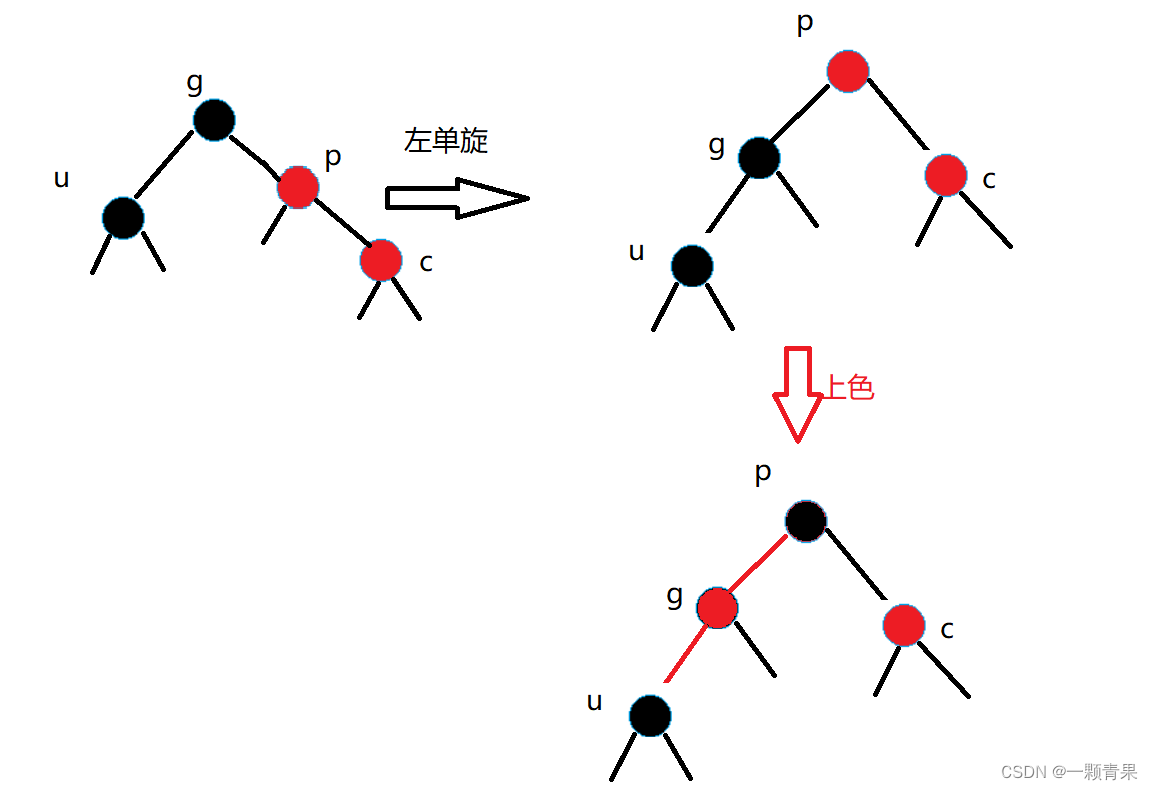
🍒🍒4.2.5情况四：

cur为红，p为红，g为黑，u不存在/u存在且为黑，p是g的右孩子，cur是p的右孩子

解决方案：

1. 先对grandparent进行左单旋
2. 再将parent变黑，grandparent变红

🍒🍒4.2.6情况五：

cur为红，p为红，g为黑，u不存在/u存在且为黑，p是g的右孩子，cur是p的左孩子

重点提醒：

               可以发现右单旋后就变成了情况四

解决方案：

1. 先对parent进行右单旋
2. 再对grandparent进行左单旋
3. 最后将cur变黑，grandparent变红，这里将cur变黑而不是parent是因为左单旋后cur取代了parent的位置

5.红黑树的验证

1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)

void Inorde(AVLNode * root, vector<pair<K, V>>&v)
{if (root == nullptr)return;Inorde(root->_left, v);v.push_back(root->_val);Inorde(root->_right, v);
}

2. 检测其是否满足红黑树的性质

bool IsBalance(Node*root)
{//空树也是红黑树if (root == nullptr)return true;//违反性质2if (root->_col == RED){cout << "树的根节点应该是黑色，可该树却是红色" << endl;return false;}//计算一条路径黑节点数量Node* cur = root;int num = 0;while (cur){if (cur->_col == BLACK)num++;cur = cur->_left;}return _IsBlance(root, num);
}
IsBalance(Node* root, size_t num, size_t cur_num)
{if (root == nullptr){//违反性质4if (num != cur_num){cout << "对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点，但该树却不是" << endlreturn false;}elsereturn true;}if (root->_col == BLACK)num++;//违反性质3if (root->_parent && root->_parent == RED && root->_col == RED){cout << "如果一个节点是红色的，则它的两个孩子结点是黑色的,可该树却出现了连续的红色节点" << endl;return false;}return IsBalance(root->_left, num, cur_num) && IsBalance(root->_right, num, cur_num);
}

6. 红黑树与AVL树的比较

这篇关于【C++进阶】红黑树的复仇（红与黑的爱恨厮杀）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！