本文主要是介绍多叉树题目:N 叉树的最大深度,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:N 叉树的最大深度
出处:559. N 叉树的最大深度
难度
3 级
题目描述
要求
给定一个 N 叉树,返回其最大深度。
最大深度是从根结点到最远叶结点的最长路径上的结点数。
N 叉树在输入中按层序遍历序列化表示,每组子结点由空值 null \texttt{null} null 分隔(请参见示例)。
示例
示例 1:
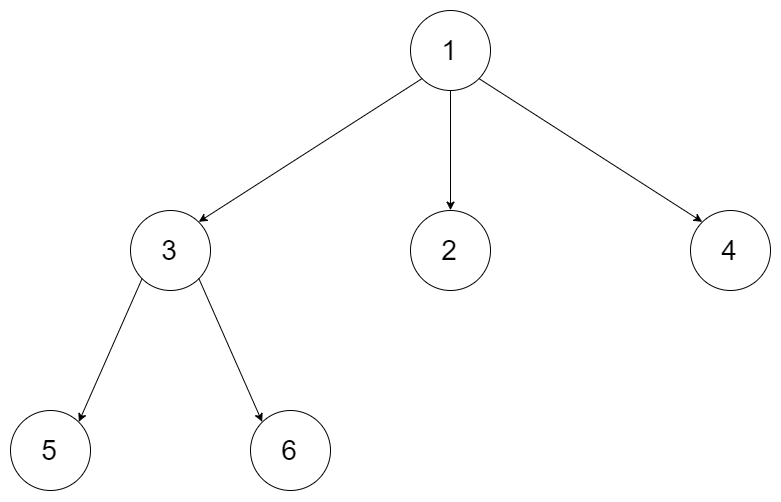
输入: root = [1,null,3,2,4,null,5,6] \texttt{root = [1,null,3,2,4,null,5,6]} root = [1,null,3,2,4,null,5,6]
输出: 3 \texttt{3} 3
示例 2:
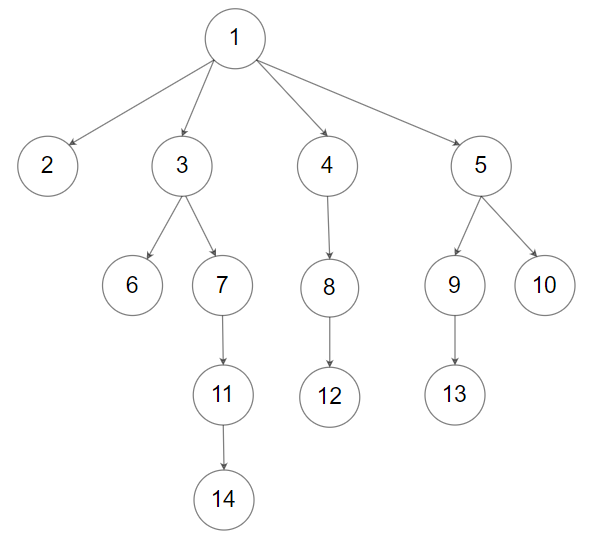
输入: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] \texttt{root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]} root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出: 5 \texttt{5} 5
数据范围
- 树中结点数目在范围 [0, 10 4 ] \texttt{[0, 10}^\texttt{4}\texttt{]} [0, 104] 内
- N 叉树的高度小于或等于 1000 \texttt{1000} 1000
解法一
思路和算法
如果 N 叉树为空,则深度为 0 0 0。对于非空 N 叉树,首先计算每个子树的最大深度,子树最大深度的最大值加 1 1 1 即为 N 叉树的最大深度,每个子树的最大深度可以使用同样的方式计算。因此可以使用深度优先搜索计算 N 叉树的最大深度。
计算 N 叉树的最大深度的过程是一个递归的过程,递归的终止条件是 N 叉树为空,此时 N 叉树的最大深度为 0 0 0。对于非空 N 叉树,首先递归地计算每个子树的最大深度,然后将子树最大深度的最大值加 1 1 1 即为 N 叉树的最大深度。
代码
class Solution {public int maxDepth(Node root) {if (root == null) {return 0;}int childDepth = 0;List<Node> children = root.children;for (Node child : children) {childDepth = Math.max(childDepth, maxDepth(child));}return childDepth + 1;}
}
复杂度分析
-
时间复杂度: O ( m ) O(m) O(m),其中 m m m 是 N 叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( m ) O(m) O(m),其中 m m m 是 N 叉树的结点数。空间复杂度主要是递归调用的栈空间,取决于 N 叉树的高度,最坏情况下 N 叉树的高度是 O ( m ) O(m) O(m)。
解法二
思路和算法
也可以使用广度优先搜索计算 N 叉树的最大深度。
广度优先搜索需要使用队列存储待访问的结点,初始时将根结点入队列。最简单的广度优先搜索的做法是,每次将一个结点出队列,然后将该结点的子结点入队列,直到队列为空时遍历结束。
这道题需要计算 N 叉树的最大高度,因此在广度优先搜索的过程中需要维护深度的信息,实现和最简单的广度优先搜索有所不同。为了维护深度信息,需要确保每一轮访问的结点为同一层的全部结点。
初始时,队列内只有根结点,是同一层的全部结点。每一轮访问结点之前需要首先得到队列内的元素个数,此时队列内的元素为同一层的全部结点,然后访问这些结点,并将这些结点的子结点入队列。一轮访问结束之后,当前层的全部结点都已经出队列并被访问,此时队列内的元素为下一层的全部结点,下一轮访问时即可访问下一层的全部结点。使用上述做法,可以确保每一轮访问的结点为同一层的全部结点。
在确保每一轮访问的结点为同一层的全部结点的情况之下,根据访问的总轮数即可得到 N 叉树的最大深度,其中根结点的深度为 1 1 1。
代码
class Solution {public int maxDepth(Node root) {if (root == null) {return 0;}int depth = 0;Queue<Node> queue = new ArrayDeque<Node>();queue.offer(root);while (!queue.isEmpty()) {depth++;int size = queue.size();for (int i = 0; i < size; i++) {Node node = queue.poll();List<Node> children = node.children;for (Node child : children) {queue.offer(child);}}}return depth;}
}
复杂度分析
-
时间复杂度: O ( m ) O(m) O(m),其中 m m m 是 N 叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( m ) O(m) O(m),其中 m m m 是 N 叉树的结点数。空间复杂度主要是队列空间,队列内元素个数不超过 n n n。
这篇关于多叉树题目:N 叉树的最大深度的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





