本文主要是介绍Day25:回溯法 LeedCode216.组合总和III 17.电话号码的字母组合,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
216. 组合总和 III
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
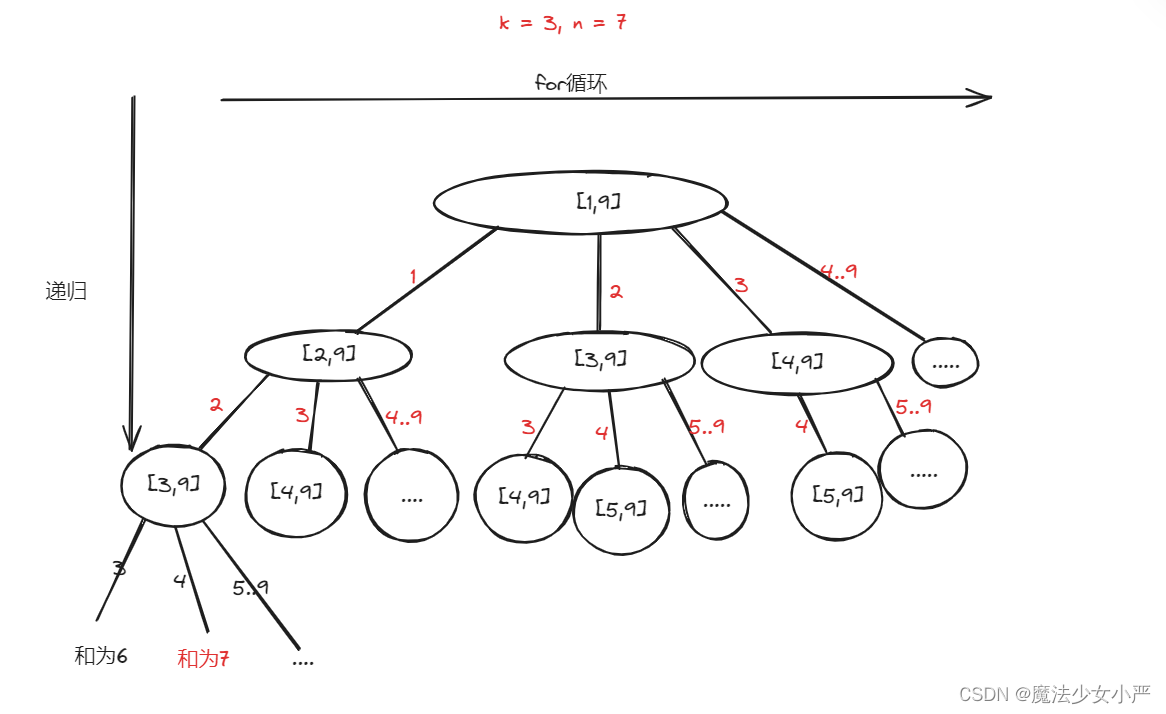
输入: k = 3, n = 7 输出: [[1,2,4]] 解释: 1 + 2 + 4 = 7 没有其他符合的组合了。
思路:本题与77.组合思路一致,无非就是多了一个和的限制
递归三部曲:
1.确定返回值和参数的类型
用全局变量List<List<Integer>> result 和List<Integer> path记录路径和结果,无需返回值,需要传入k(树的深度/数的目标个数),targetSum(目标和),startIndex(为下一层for循环搜索的起始位置),sum(当前和)
void backtracking(int targetSum,int sum,int k,int startIndex)
2.确定结束条件
遍历到path.size()==k时,判断该路径是否加入结果,结束递归
if(path.size()==k){
if(targetSum==sum)
result.add(new ArrayList(path));
return;
}
3.单层递归逻辑
for循环横向遍历,递归纵向遍历,本题和77.组合区别之一就是集合固定的就是9个数[1,...,9],所以for循环固定i<=9,处理过程就是 path收集每次选取的元素
for(int i=startIndex;i<10;i++){
sum+=i;
path.add(i);
backtracking(targetSum,sum,k,i+1);
sum-=i;
path.removeLast();
代码参考:
class Solution {List<List<Integer>> result;List<Integer> path;public List<List<Integer>> combinationSum3(int k, int n) {path=new LinkedList<>();result=new ArrayList<>();backtracking(n,0,k,1);return result;}void backtracking(int targetSum,int sum,int k,int startIndex){if(path.size()==k){if(targetSum==sum)result.add(new ArrayList(path));return;}for(int i=startIndex;i<10;i++){sum+=i;path.add(i);backtracking(targetSum,sum,k,i+1);sum-=i;path.removeLast();}}
}代码优化:
剪枝:
当剩下的数的个数不够用时path.size()+9-i+1<k时结束递归
当sum>targetSum时结束递归
class Solution {List<List<Integer>> result;List<Integer> path;public List<List<Integer>> combinationSum3(int k, int n) {path=new LinkedList<>();result=new ArrayList<>();backtracking(n,0,k,1);return result;}void backtracking(int targetSum,int sum,int k,int startIndex){if(targetSum<sum) return;//剪枝if(path.size()==k){if(targetSum==sum)result.add(new ArrayList(path));return;}
//剪枝for(int i=startIndex;i<=path.size()+9-k+1;i++){sum+=i;path.add(i);backtracking(targetSum,sum,k,i+1);sum-=i;path.removeLast();}}
}17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例 1:
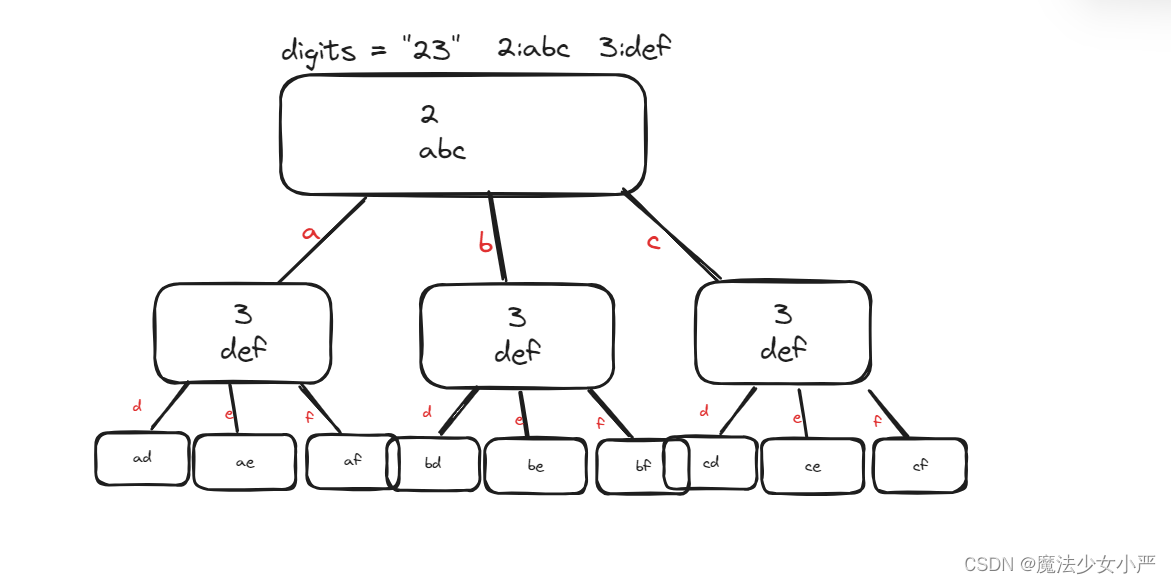
输入:digits = "23" 输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
思路:本题要思考几个问题
1.如何将字母和数字对应
用一个字符数组存储每个数字对应的字符串
numToString=new String[]{"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
将数字转为对应的字符串
String str=numToString[digits.charAt(index)-'0'];
2.两个数字需要两层循环,三个数字三层循环,如何根据个数实现几层循环
用回溯法,根据是否遍历完digits的每个数字决定是否进行for循环
if(digits.length()==index){
result.add(temp.toString());
return;
递归三部曲:
1.确定返回值和参数类型
无需返回值,用全局变量List<String> result记录结果 ,传入digits(数字字符串)和index(表示这层循环从哪个数字开始)
全局遍量 String[] numToString记录数字和字符串的对应关系
2.确定递归结束条件
当index==digits.length时结束递归,
如果digits为null或者空串时,返回空List<String> result
if(digits==null||digits.length()==0){
return ;
}
3.确定单层逻辑
首先要取index指向的数字,并找到对应的字符集(手机键盘的字符集)。
然后for循环来处理这个字符集,代码如下:
//将数字转为对应的字符串
String str=numToString[digits.charAt(index)-'0'];
//遍历字符串
for(int i=0;i<str.length();i++){
//将字符加入
temp.append(str.charAt(i));
//回溯
backtracking(digits,index+1);
temp.deleteCharAt(temp.length() - 1);
}
代码参考:
class Solution {List<String>result;String[] numToString;StringBuilder temp=new StringBuilder();public List<String> letterCombinations(String digits) {numToString=new String[]{"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};result=new ArrayList<>();backtracking(digits,0);return result;}void backtracking(String digits,int index){if(digits==null||digits.length()==0){return ;}//遍历完digits的每个数字,结束递归if(digits.length()==index){result.add(temp.toString());return;}//将数字转为对应的字符串String str=numToString[digits.charAt(index)-'0'];//遍历字符串for(int i=0;i<str.length();i++){//将字符加入temp.append(str.charAt(i));//回溯backtracking(digits,index+1);temp.deleteCharAt(temp.length() - 1);}}
}
这篇关于Day25:回溯法 LeedCode216.组合总和III 17.电话号码的字母组合的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




