本文主要是介绍[数字图像处理]数字图像的整数倍扩大(数字图像插值)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
1.序言
在不同的平台下，或者从不同仪器获得图像（或者数据），其大小与数据类型，都有着很大的不同。这里的 大小，就是指的是分辨率。 数字图像，其实是像素的集中表现形式，像素越多越密集，图像则可以表现得越精确的。我们将数字图像的像素数，称为分辨率。
本文主要介绍了数字图像的整数倍扩大（也就是分辨率的变化）。事实上，扩大处理可以归结为，新的像素值的如何决定的插值问题。首先，作为目标，先对理想的插值进行理解。然后，对现有的常用插值方法进行一个讨论，对其性能进行全面的分析。
2.理想的插值处理
首先，作为目标，先对理想的插值进行说明。为了便于理解，我们假设有如下这样一个模拟信号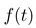
。
。
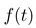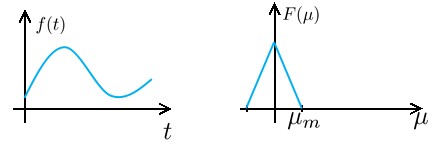
左边是我们假设的模拟型号在时间域内的表现，右边是其频谱。先这样假设着，然后，我们将这个信号进行采样。
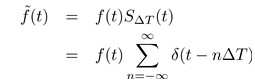
这里，
是一个冲击串函数，所得到的是一个离散的信号
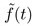。如下所示，求所得到的离散信号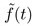的离散傅里叶变换。
是一个冲击串函数，所得到的是一个离散的信号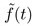。如下所示，求所得到的离散信号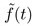的离散傅里叶变换。
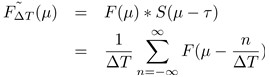
看上式，并求其离散信号的振幅谱，所得到的振幅谱变为了一个周期性的，表示为如下形式。
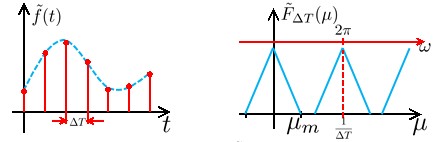
这里，我们选择的采样时间间隔为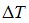
。一般的，还会将得到的振幅谱归一化，将横轴变为归一化频率。所得到的振幅谱的两个波峰之间差一个2π。
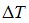。一般的，还会将得到的振幅谱归一化，将横轴变为归一化频率。所得到的振幅谱的两个波峰之间差一个2π。
为了说明理想插值，我们假设如下两个信号。首先，选择采样间隔时间为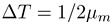
，可以得到如下信号①。
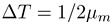，可以得到如下信号①。
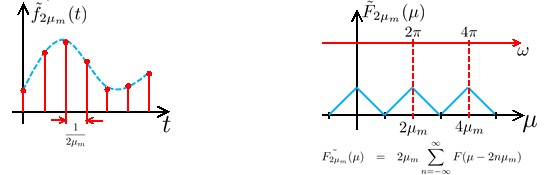
然后，将其采样时间间隔设置为0.5倍（也就是将采样频率设置为信号①的2倍），也就是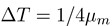
，可以得到如下的信号②。
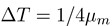，可以得到如下的信号②。
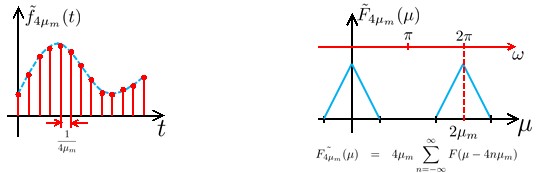
观察上述两个信号，①与②。我们可以得到这样两个信息。一，两个波峰之间的归一化频率的差都是2π。二，信号②的振幅是信号①的两倍。对于理想的插值处理，我们进行如下定义。
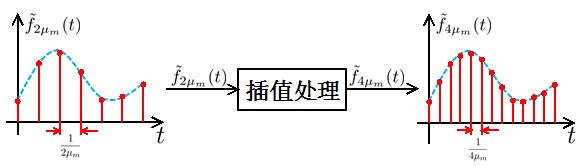
如果通过某个处理，可以从信号①变换到信号②的话，这样的插值处理就称为理想插值。
下面，从频域上来观察一下理想插值处理。如下图所示，
最左边是信号①的频谱，最右边是信号②的频谱（也就是目标信号）。首先，在信号①的时间域的相邻的信号中间，依次插入1个0（扩大倍率是U的时候，插入0的个数是U-1个0。上述例子的U为2，故插入一个0。），所得到的信号的振幅谱就像中间的那样
这篇关于[数字图像处理]数字图像的整数倍扩大(数字图像插值)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
![[OpenCV] 数字图像处理 C++ 学习——13Canny边缘检测 附完整代码](https://i-blog.csdnimg.cn/direct/a81548c3b63146cc8c6ce4f9e4b78619.png#pic_center)
