本文主要是介绍B样条曲线(记录),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

B样条曲线的生成靠的两点:
1、控制点
2、基函数
B样条曲线的基函数是一个De Boor的递归表达式[1]:
(1)
(2)
其中是第
个
阶基函数。
而B样条曲线可以表示为[2]:
(3)
如何理解上式?首先,我们知道,如果一个函数在定义域内处处可微(处处连续),则可以通过被泰勒展开成一个多项式级数。换言之,只要阶数足够,对于任意的连续可微曲线,都可以用一个多项式去逼近。B样条曲线的表达式就是一个阶多项式。它的定义域通过节点区间来表示[1][2]。
接下来,我们通过一个简单的例子来逐步理解B样条曲线。
我们以3个控制点的B样条曲线为例。其表达式为:
现在我们来看一下上式的3个基函数。由式(2),我们可知阶的基函数如下图:
阶基函数的个数为:
,简单归纳一下:
设为控制点的个数,则
阶的基函数个数也为
,而
阶的基函数个数为:
。即低一阶的基函数个数是高一阶加一。则
阶的基函数的个数为:
。
另外,对于多项式的阶,必须小于已知数据点数的个数。于是我们设。则
阶的基函数个数为
,为奇数。
接下来,我们来看看节点区间。对于阶基函数,一个基函数对应一个节点区间。所以节点区间的个数,我们以3个
阶基函数为例:

为3个区间,共计4个节点,也即节点数为0阶基函数个数加一,即个节点。
另外,当我们选取一个参数时,由于节点区间不相交,所以我们由式(1)可知0阶基函数,由且只有一个基函数的值为1。其余皆为0。考虑如下情况:

当取在区间
时,我们可以发现在1阶基函数,所有基函数相机等于1。因为0阶基函数只有一个起作用,而其余基函数的值为0.递推到1阶,所有1阶基函数,变为2个基函数起作用。而这两个基函数相加:
。
同理,到了2阶基函数,我们可以得到:
也即2阶基函数相加也等于1。以此类推,我们得出一个结论,d阶基函数相加等于1。
现在来考虑如下的递归过程。假设我们有4个控制点,阶数。于是基函数的传递如下:

假如我们把u取在内,则
,而其余0阶基函数为0。按照以上的结论,我们知道
,而实际上,没有
。于是到了1阶,基函数之和不等于1。而且每进一阶,基函数之和都会有损失。
同时,我们还希望,当u取或者
时,曲线与控制点0或者控制点n重合。换句话说,就是曲线在端点处与控制点重合,也即
,而其余3阶基函数等于0。很明显,
无法使以上条件成立。为了实现以上条件,必须解决基函数之和损失的问题。那么u就必须取在区间
内。当
时,递归到3阶可得
,而其余为0。当
时,递归到3阶可得
,而其余为0。因此为了满足基函数之和为1。而且当u取在区间端点时,曲线与控制点重合。我们必须舍弃
之外的区间。这个操作叫“重复度”。具体的操作是令
之前的节点都等于
。而
之后的节点都等于
。也即
区间之外,其余区间节点都分别赋值
。
例如,原本各区间为。进行“重复度”操作后,节点区间变为:
,甚至干脆,我们取
。
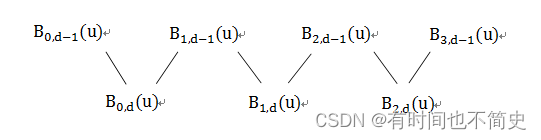
接下来,我们设,我们可以得到如下的基函数系数传递图:

则我们可以得到d阶第个基函数为
,其中
为如下分布的系数:

以上三角序列为杨辉三角序列,因此。
参考:
1、样条曲线曲面-3:BSpline的原理
2、详解B样条曲线
这篇关于B样条曲线(记录)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






