回溯dfs和分支限界bfs

本文主要是介绍回溯dfs和分支限界bfs，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一：拓扑排序

207. 课程表

这道题说白了就是在有向图中找环

拓扑排序实际上应用的是贪心算法。

贪心算法简而言之：每一步最优，全局就最优。

• 每一次都从图中删除没有前驱的顶点，这里并不需要真正的删除操作，通过设置入度数组。

• 每一轮都输出入度为 0的结点，并移除它，同时修改它指向的结点的入度（−1-即可）

  —依次得到的结点序列就是拓扑排序的结点序列

  如果图中还有结点没有被移除，则说明“不能完成所有课程的学习”。

拓扑排序顺序

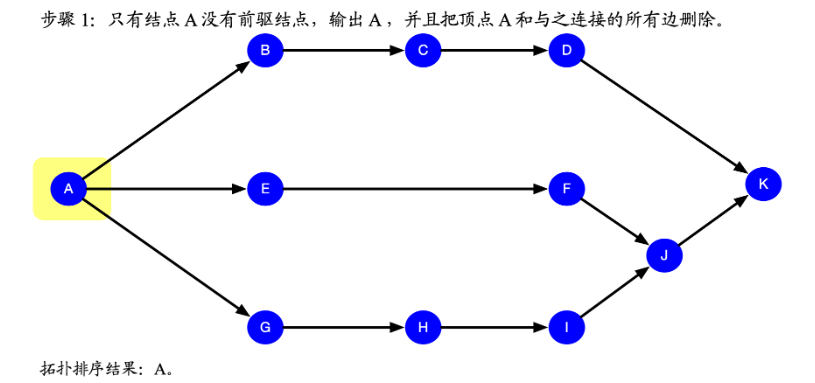
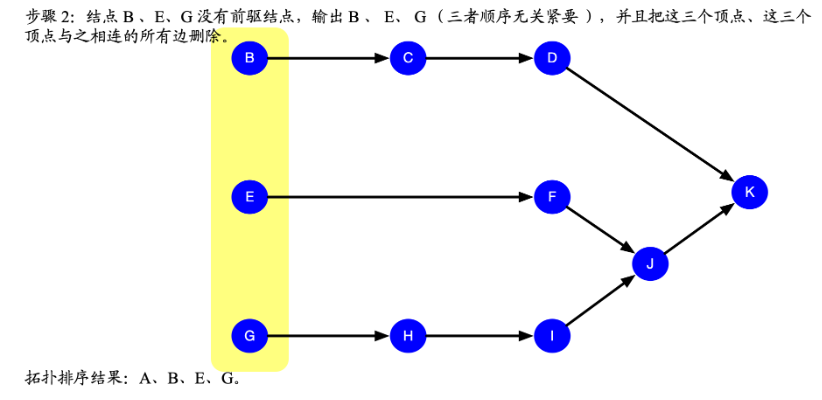
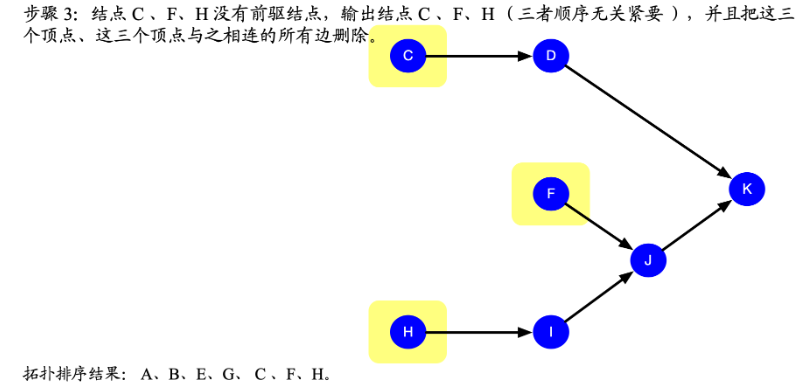
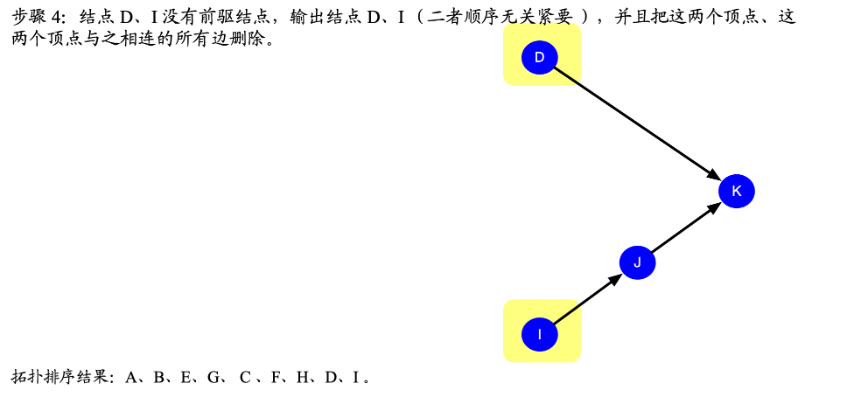
最后的排序结果

拓扑排序不能输出所有结点就说明原来的有向图有环

有环必存在一条边指向，不满足入度为0，也就不会输出

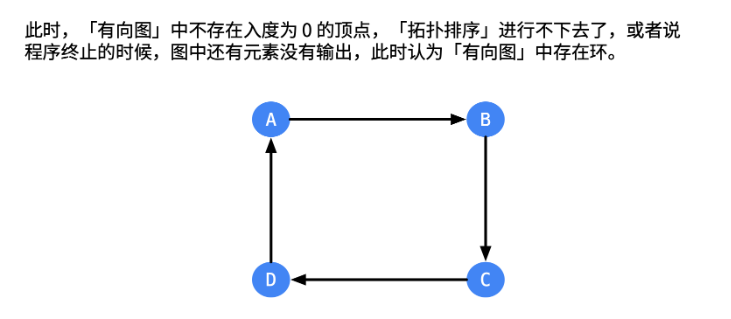
本题解法：

class Solution {
public:bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {vector<vector<int>> graph(numCourses,vector<int>());//建立入度数组vector<int> indegree(numCourses);//创建图：[u,v]---v->ufor(auto val:prerequisites){int u=val[0];int v=val[1];graph[v].push_back(u);indegree[u]++;//更新入度}queue<int> que;//装顶点，也就是下标//入读为0的节点入队for(int i=0;i<numCourses;i++){if(indegree[i]==0) que.push(i);}while(!que.empty()){auto x=que.front();que.pop();//说明一门课程满足结果numCourses--;for(auto val:graph[x]){indegree[val]--;//移除边//把入度为0的结点入队if(indegree[val]==0){que.push(val);}}}return numCourses==0;}
};

也可以用map<顶点，顶点的出边指向点集合>来创建图

class Solution {
public:bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {//set(顶点)=顶点的出边unordered_map<int,set<int>> mp;//建立入度数组vector<int> indegree(numCourses);//创建图：[u,v]---v->ufor(auto val:prerequisites){int u=val[0];int v=val[1];mp[v].insert(u);//这里是set要用insertindegree[u]++;//更新入度}queue<int> que;//装顶点，也就是下标//入读为0的节点入队for(int i=0;i<numCourses;i++){if(indegree[i]==0) que.push(i);}int col=0;while(!que.empty()){auto x=que.front();que.pop();//说明一门课程满足结果col++;for(auto val:mp[x]){indegree[val]--;//移除边//把入度为0的结点入队if(indegree[val]==0){que.push(val);}}}return col==numCourses;}
};

矩阵最长路径

329. 矩阵中的最长递增路径

这道题的难点在于：把矩阵抽象成图，然后对图进行拓扑排序，就可以得到所求

• 抽象成图

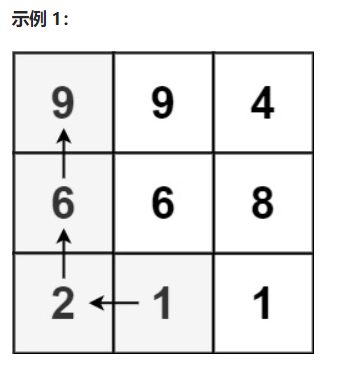
把m×n的矩阵中每一个值作为图的顶点，顶点数设置为i×n+j，那么对于每个点进行上下左右遍历，只要值大于它，也就是满足了单调递增的条件，就指向它。

比如：

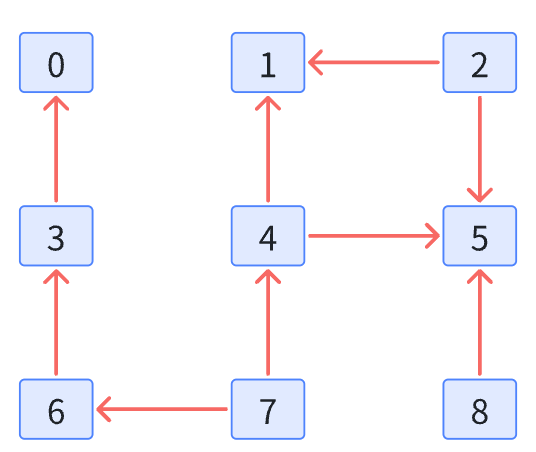
可以抽象成：

• 对创建好的图进行拓扑排序

解答：

class Solution {
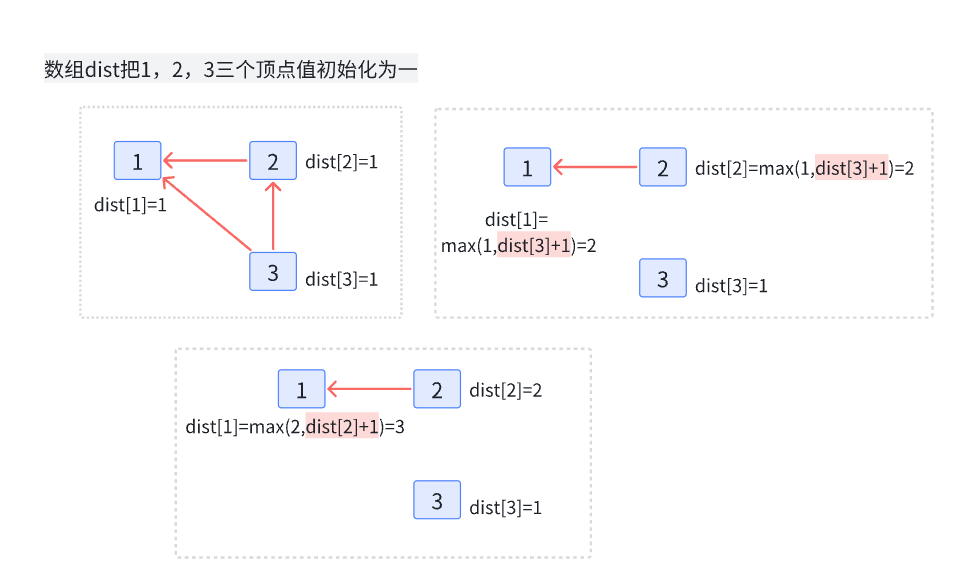
public:int longestIncreasingPath(vector<vector<int>>& matrix) {/*创建图*/this->m=matrix.size();this->n=matrix[0].size();//注意：结点数是m*nthis->graph=vector<vector<int>>(m*n,vector<int>());//遍历结点加边顺便统计入度indegree=vector<int>(m*n,0);for(int i=0;i<m;i++){for(int j=0;j<n;j++){addEdge(matrix,i,j);}}/*拓扑排序*/queue<int> que;vector<int> dist(m*n,1);//长度包含自己，最小1//结点为0入队for(int i=0;i<m*n;i++){if(indegree[i]==0) que.push(i);}//去掉该节点的出边，选择其他的入度为0结点while(!que.empty()){int tmp=que.front();que.pop();for(auto& val:graph[tmp]){indegree[val]--;//指向结点dist更新dist[val]=max(dist[val],dist[tmp]+1);if(indegree[val]==0){que.push(val);}}}/*遍历dist,取最大*/int ans=0;for(int i=0;i<m*n;i++){ans=max(ans,dist[i]);}return ans;}
private:int m,n;vector<int> indegree;vector<vector<int>> graph;int getNode(int x,int y){ return x*n+y;};int d[4][2]={{1,0},{-1,0},{0,1},{0,-1}};bool isInArea(int x,int y){return x>=0 && y>=0 && x<m && y<n;}void addEdge(vector<vector<int>>& matrix,int x,int y){for(int i=0;i<4;i++){int nx=x+d[i][0];int ny=y+d[i][1];if(isInArea(nx,ny)&& matrix[x][y]<matrix[nx][ny]){int u=getNode(x,y);int v=getNode(nx,ny);graph[u].push_back(v);indegree[v]++;//入度++}}} 
};

二：求树的每一层的最大值

515. 在每个树行中找最大值

很明显要分清每一层的结点，然后比较同层的值

每次循环的队列值就是当前层结点

   vector<int> largestValues(TreeNode* root) {vector<int> res;if(root==NULL) return res;queue<TreeNode*> que;que.push(root);while(!que.empty()){int sz=que.size();int n=INT_MIN;while(sz-->0){auto tmp=que.front();que.pop();n=max(n,tmp->val);if(tmp->left) que.push(tmp->left);if(tmp->right) que.push(tmp->right);}res.push_back(n);}return res;}

也可以用深度优先遍历来做，注意层高

class Solution {
public:vector<int> largestValues(TreeNode* root) {//if(root==NULL) return res;dfs(root,0);//注意从0开始return res;}
private:vector<int> res;void dfs(TreeNode* root,int h){if(root==NULL) return;//合法性检查：res[]要符合if(h==res.size()){res.push_back(INT_MIN);}//存放结果res[h]=max(res[h],root->val);//递归dfs(root->left,h+1);dfs(root->right,h+1);}
};

三：搜索问题知识点

搜索是一种枚举的算法，所有不能多项式时间求解的NP问题都需要靠搜索求解

定义搜索框架会极大地帮助学习动态规划和图论算法

状态空间图

状态：对问题在某一时刻的进展情况的数学描述，从一种状态转移到另一种（或几种）状态的操作叫：状态转移

状态空间就是在搜索过程中所有状态的集合

本质上,状态就是程序中程序所维护的所有动态数据结构的集合

注意状态只关注动态的数据

如果其他信息可以通过其他数据决定，那么只关注最根本的信息

如果把状态视为一个点，从一个状态可以到达另一个状态就连一条边，那么整个状态空间就是一张有向图

• 节点是搜索问题中定义的状态
• 边代表动作所导致的转换

----对状态空间的搜索就相当于对状态空间图进行遍历

搜索题解题步骤：

先提取动态变量，找出最基本的变量（不会被其他变量所确定），然后确定遍历顺序

子集和排列的状态空间

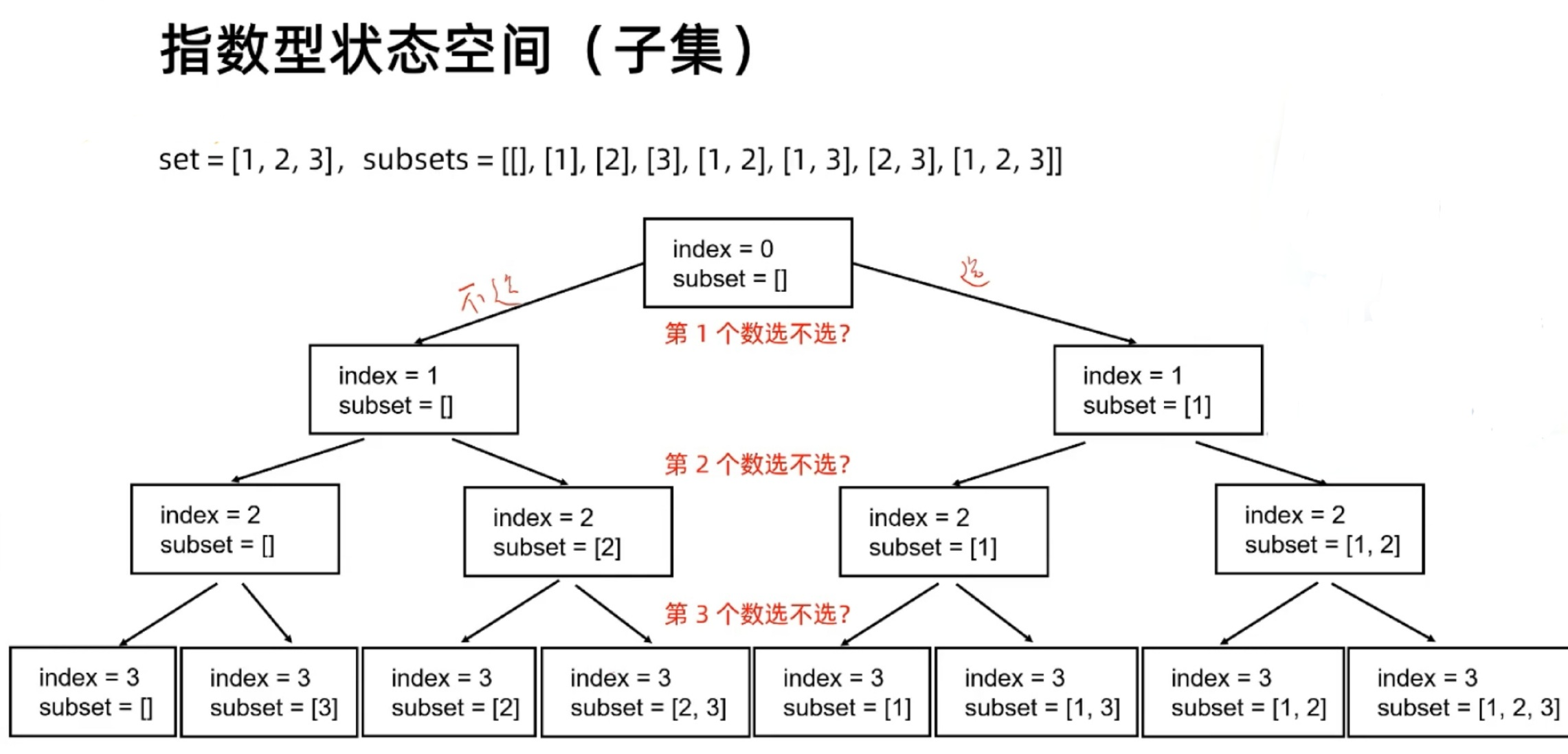
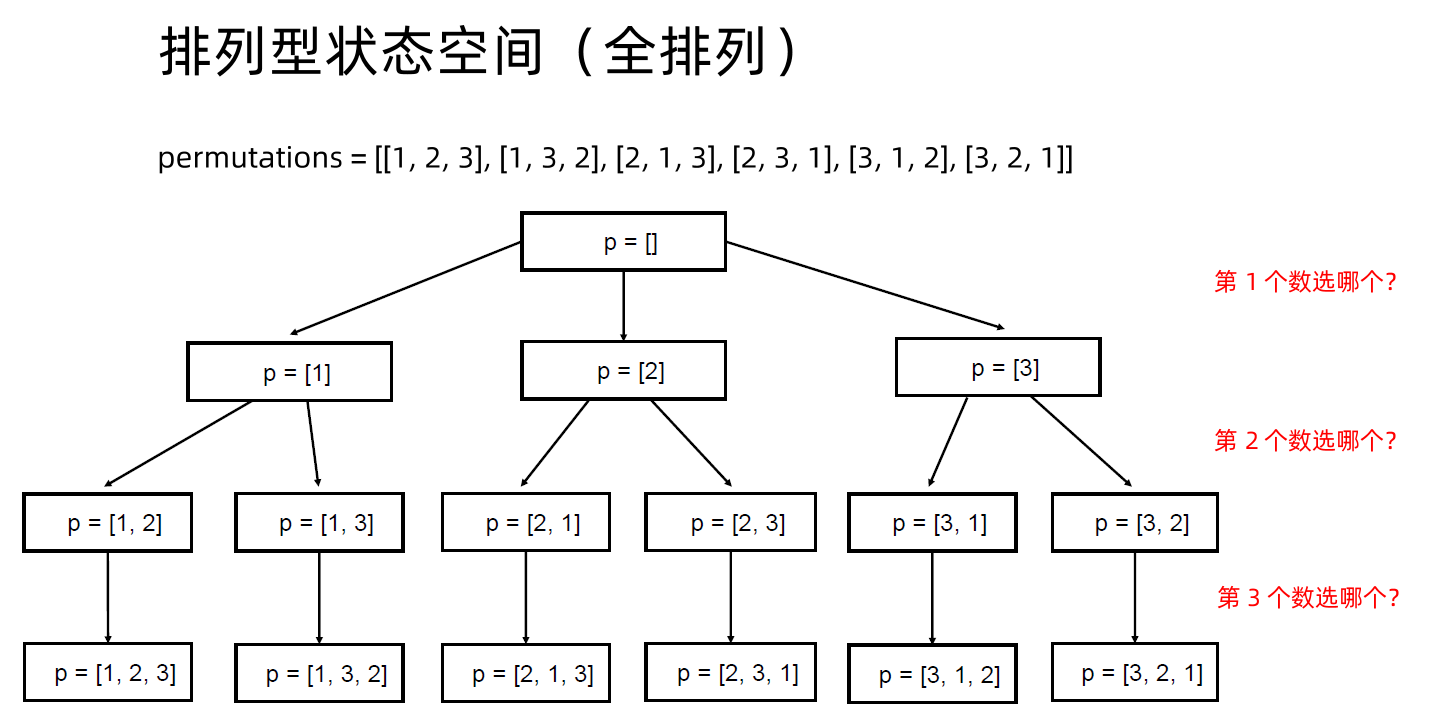
搜索其实就是遍历整个状态空间图来寻找答案的一类算法，可以分为深度优先遍历和广度优先遍历。

一般来说：一种状态只需要遍历一次，所以如果状态空间图不是树，就需要判重，也就是记忆化。

四：搜索问题力扣题

电话号码组合

17. 电话号码的字母组合

​ 本题属于子集类型的回溯，每个字母有若干个字符，最后只从其中选一个。所以递归参数需要数字i，表示当前访问的第i个数字。

class Solution {
public:const string letterMap[9]{//letter[1]对应2"","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};vector<string> letterCombinations(string digits) {this->digits=digits;if(digits=="") return res;dfs(0);return res;}
private:string digits;string ans;vector<string> res;void dfs(int index){//第index数字if(index==digits.size()){res.push_back(ans);return;//别忘了满足题目要求后需要return}int x=digits[index]-'0';string tmp=letterMap[x-1];for(int i=0;i<tmp.size();i++){ans+=tmp[i];dfs(index+1);ans.pop_back();}}
};

当然也可以用map存储，更直观一些

class Solution {
public:vector<string> letterCombinations(string digits) {this->digits=digits;//定义mapmp['2']="abc";        mp['3']="def";mp['4']="ghi";mp['5']="jkl";mp['6']="mno";mp['7']="pqrs";mp['8']="tuv";mp['9']="wxyz";     if(digits=="") return res;dfs(0);return res;}
private:string digits;string ans;unordered_map<char,string> mp;vector<string> res;void dfs(int index){//第index数字if(index==digits.size()){res.push_back(ans);return;//别忘了满足题目要求后需要return}string tmp=mp[digits[index]];//mp[digits对应的数字]for(int i=0;i<tmp.size();i++){ans+=tmp[i];dfs(index+1);ans.pop_back();}}
};

n皇后

51. N 皇后

思路：其实就是全排列的基础上加上不能选上一个对应的两个对角线位置

同一个对角线的特点，要么和为定值，要么差为定值

n×n的一面对角线个数：2×n-1

和为定值

差为定值

用数组存储注意有负数，需要加上n-1

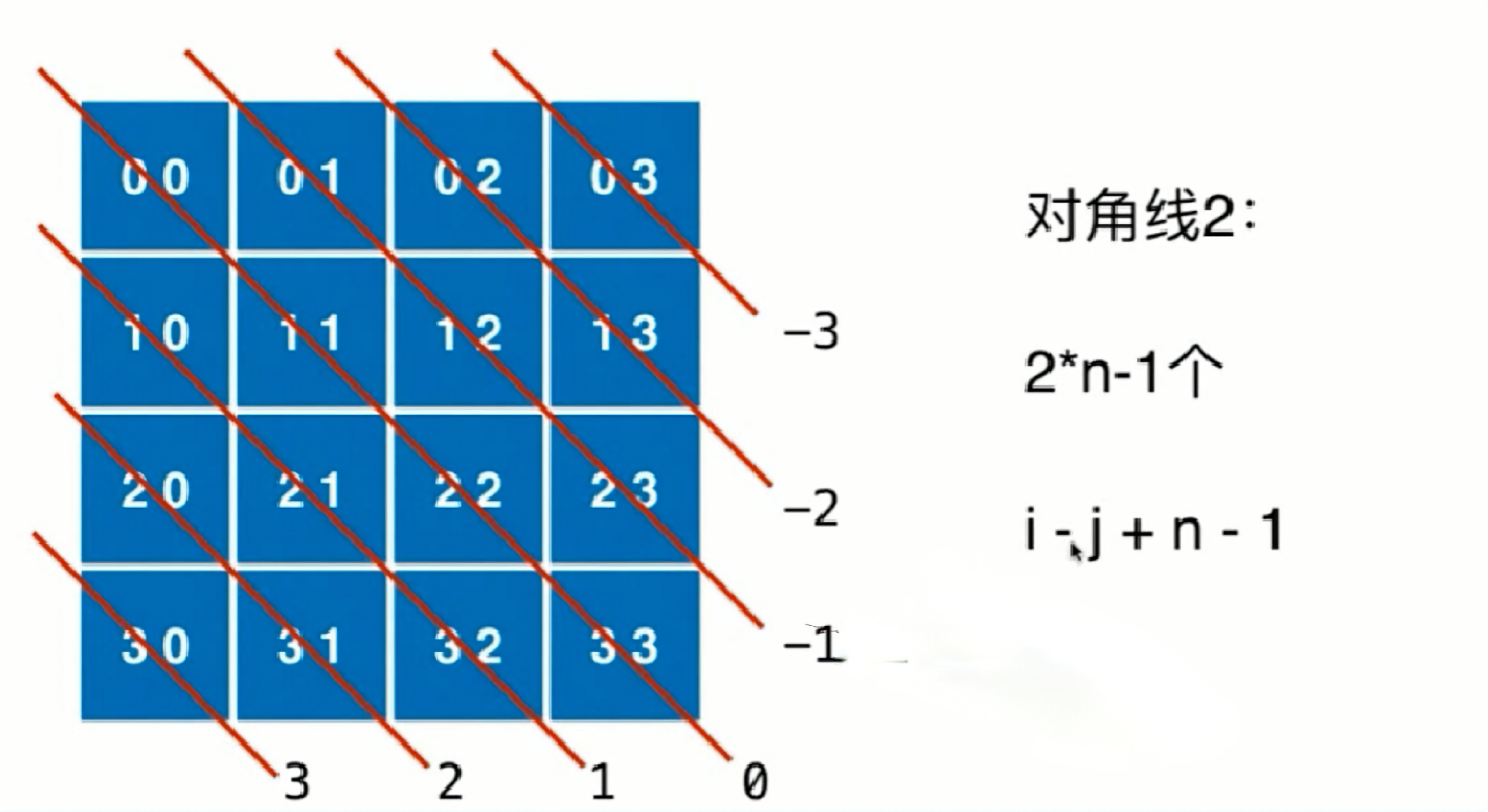
class Solution {
public:vector<vector<string>> solveNQueens(int n) {this->n=n;this->visit=vector<bool>(n,false);this->dig_sum=vector<bool>(n*2-1,false);this->dig_minus=vector<bool>(n*2-1,false);dfs(0);//把数字对应成棋盘//比如1302对应：.Q..|...Q|Q...|..Q.vector<vector<string>> res;for(auto val:vec){//一个数字排列vector<string> tmp;for(auto x:val){string ss(n,'.');ss[x]='Q';tmp.push_back(ss);}res.push_back(tmp);}return res;}
private://先写出不同行不同列不同对角线的全排列int n;vector<vector<int>> vec;vector<int> ans;vector<bool> visit;//两个对角线---撇是下标和相同，捺是下标差相同//注意：n×n的棋盘有：2*n-1个对角线vector<bool> dig_sum;//注意差下标有负数，所以加上n-1 (0,n-1)vector<bool> dig_minus;void dfs(int index){if(ans.size()==n){vec.push_back(ans);return;}for(int i=0;i<n;i++){if(!visit[i]&&!dig_sum[i+index]&&!dig_minus[n-1+i-index]){visit[i]=true;dig_minus[i-index+n-1]=true;dig_sum[i+index]=true;ans.push_back(i);dfs(index+1);ans.pop_back();dig_minus[i-index+n-1]=false;dig_sum[i+index]=false;visit[i]=false;}}}
};

当然也可以用map，map不必考虑下标为负数情况

      unordered_map<int,bool> dig_plus;unordered_map<int,bool> dig_minus;//直接i+index和i-index(或index-i)for(int i=0;i<n;i++){if(!visit[i]&&!dig_plus[i+index]&&!dig_minus[i-index]){visit[i]=true;dig_minus[i-index]=true;dig_plus[i+index]=true;ans.push_back(i);dfs(index+1);ans.pop_back();dig_minus[i-index]=false;dig_plus[i+index]=false;visit[i]=false;}}

这里也可以每次得到一个vector后直接存储vector

class Solution {
public:vector<vector<string>> solveNQueens(int n) {this->n=n;this->visit=vector<bool>(n,false);dfs(0);return res;}
private://先写出不同行不同列不同对角线的全排列int n;vector<vector<string>> res;vector<int> ans;vector<bool> visit;unordered_map<int,bool> dig_plus;unordered_map<int,bool> dig_minus;vector<string> qipan(vector<int>& ans){//[1,2,3,4]vector<string> board(n,string(n,'.'));for(int i=0;i<n;i++){board[i][ans[i]]='Q';}return board;}void dfs(int index){if(ans.size()==n){//在这里把一个ans结果变成棋盘res.push_back(qipan(ans));return;}for(int i=0;i<n;i++){if(!visit[i]&&!dig_plus[index-i]&&!dig_minus[i+index]){visit[i]=true;dig_minus[i+index]=true;dig_plus[index-i]=true;ans.push_back(i);dfs(index+1);ans.pop_back();dig_minus[i+index]=false;dig_plus[index-i]=false;visit[i]=false;}}}
};

地图类搜索----岛屿数量

200. 岛屿数量

每次dfs都可以找到一个连通分支，因为dfs的递归结果就是连通树或者连通图

本题思路：

对整张图进行dfs搜索，dfs搜索次数就是符合题目要求的数量

dfs回溯时注意：

这里每一个点（x,y两个方向）,都可以向上左右移动，这里边界（四周）有移动越界问题

所以可以继续进行dfs的条件是：

• (x,y)运动后的坐标不越界
• 移动后的(x,y)对应的结点没有访问过
• 移动后的(x,y)grid值为1不是0

而且条件之间有依赖，是否越界这个条件必须首先判断

• 也可以理解成：访问数组必须先判断下标合法性

dfs

class Solution {
public:int numIslands(vector<vector<char>>& grid) {this->m=grid.size();if(m==0) return res;this->n=grid[0].size();this->grid=grid;this->visit=vector<vector<bool>>(m,vector<bool>(n,false));//遍历整个地图for(int i=0;i<m;i++){for(int j=0;j<n;j++){//是陆地而且这个陆地没有被访问if(grid[i][j]=='1'&&!visit[i][j]){res++;//联通分量+1dfs(i,j);}}}return res;}
private:int res=0;vector<vector<char>> grid;vector<vector<bool>> visit;int m,n;//m是grid数量是宽，n是grid每一个vector的长void dfs(int x,int y){//越界returnif(x<0 || y<0 || x==m || y==n){return;}//不是陆地或者访问过 return//必须先检查越界情况if(grid[x][y]=='0' || visit[x][y]) return;//标记已经访问visit[x][y]=true;//四个方向搜索dfs(x+1,y);dfs(x-1,y);dfs(x,y+1);dfs(x,y-1);}
};

当然可以利用for循环和dx，dy来简化搜索，还可以把越界检查写成函数

int dx[4]={1,-1,0,0};int dy[4]={0,0,1,-1};bool isInArea(int x,int y){return x>=0&&y>=0&&x<m&&y<n;}void dfs(int x,int y){//越界returnif(!isInArea(x,y)){return;}if(grid[x][y]=='0' || visit[x][y]) return;//标记已经访问visit[x][y]=true;//四个方向搜索for(int i=0;i<4;i++){x+=dx[i];y+=dy[i];dfs(x,y);//回溯x-=dx[i];y-=dy[i];}}

当然可以不符合条件递归，也可以符合条件后再dfs，但是必须先判断越界然后判断陆地和是否访问过

情况1：

  int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};bool isInArea(int x, int y) { return x >= 0 && y >= 0 && x < m && y < n; }void dfs(int x, int y) {if (grid[x][y] == '0' || visit[x][y])return;// 标记已经访问visit[x][y] = true;// 四个方向搜索for (int i = 0; i < 4; i++) {x += dx[i];y += dy[i];if (isInArea(x, y))dfs(x, y);// 回溯x -= dx[i];y -= dy[i];}}

情况2：定义新变量不用回溯

 int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};bool isInArea(int x, int y) { return x >= 0 && y >= 0 && x < m && y < n; }void dfs(int x, int y) {// 标记已经访问visit[x][y] = true;// 四个方向搜索for (int i = 0; i < 4; i++) {int newx = x + dx[i];int newy = y + dy[i];if (isInArea(newx, newy) && grid[newx][newy] == '1' &&!visit[newx][newy])dfs(newx, newy);}}

bfs

和dfs一样，只不过bfs在搜索时侯，会把下一个上下左右可访问的结点入队

 int numIslands(vector<vector<char>>& grid) {int res=0;int n=grid.size();if(n==0) return 0;int m=grid[0].size();vector<vector<bool>> visit(n,vector<bool>(m,false));//遍历整个gridfor(int i=0;i<n;i++){for(int j=0;j<m;j++){//遇到0,跳出本次循环if(grid[i][j]=='0'||visit[i][j]) continue;//更新结果res++;visit[i][j]=true;//队列存放坐标值i和jqueue<pair<int,int>> que;que.push({i,j});while(!que.empty()){auto [x,y]=que.front();que.pop();//周围四个入队，注意合法性检查if(x+1<n && grid[x+1][y]=='1'&&!visit[x+1][y]){que.push({x+1,y});visit[x+1][y]=true;}if(x-1>=0 && grid[x-1][y]=='1'&&!visit[x-1][y]){que.push({x-1,y});visit[x-1][y]=true;}if(y+1<m && grid[x][y+1]=='1'&&!visit[x][y+1]){que.push({x,y+1});visit[x][y+1]=true;}if(y-1>=0 && grid[x][y-1]=='1'&&!visit[x][y-1]){que.push({x,y-1});visit[x][y-1]=true;}}//while}}return res;}

注意入队前就把周围的设置成以访问，会比出队后再设置标志节省很多时间

                  //周围四个入队，注意合法性检查visit[x][y]=true;if(x+1<n && grid[x+1][y]=='1'&&!visit[x+1][y]){que.push({x+1,y});}if(x-1>=0 && grid[x-1][y]=='1'&&!visit[x-1][y]){que.push({x-1,y});}if(y+1<m && grid[x][y+1]=='1'&&!visit[x][y+1]){que.push({x,y+1});}if(y-1>=0 && grid[x][y-1]=='1'&&!visit[x][y-1]){que.push({x,y-1});}}//while

这样的话程序时间会越界，因为一次出队相当于访问了一个结点，很慢

当然广度优先搜索可以不借助访问数组，只要每次把岛屿的1设为0即可

相当于找到1后，前后左右符合要求的入队，入队前把岛屿设为0.下一次就不再访问到了

说白了bfs就是找到一个1就把前后左右消为0，然后下一次遍历

也可以bfs设置成函数

class Solution {
public:int numIslands(vector<vector<char>>& grid) {m = grid.size();if (m == 0)return 0;n = grid[0].size();for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (grid[i][j] == '1') {grid[i][j] = '0';res++;//更新结果bfs(grid, i, j);}}}return res;}
private:int m, n;int res = 0;// grid必须可改变void bfs(vector<vector<char>>& grid, int i, int j) {queue<pair<int, int>> que;que.push({i,j});while (!que.empty()) {auto [x, y] = que.front();que.pop();// 把周围的1变成0if (x + 1 < m && grid[x + 1][y] == '1') {que.push({x + 1, y});grid[x + 1][y] = '0';}if (x - 1 >= 0 && grid[x - 1][y] == '1') {que.push({x - 1, y});grid[x - 1][y] = '0';}if (y + 1 < n && grid[x][y + 1] == '1') {que.push({x, y + 1});grid[x][y + 1] = '0';}if (y - 1 >= 0 && grid[x][y - 1] == '1') {que.push({x, y - 1});grid[x][y - 1] = '0';}}}
};

或者用4个方向

  // grid必须可改变int dx[4]={1,-1,0,0};int dy[4]={0,0,1,-1};void bfs(vector<vector<char>>& grid, int i, int j) {queue<pair<int, int>> que;que.push({i,j});while (!que.empty()) {auto [x, y] = que.front();que.pop();// 把周围的1变成0for(int i=0;i<4;i++){int nx=x+dx[i];int ny=y+dy[i];if(nx>=0 && ny>=0&& nx<m&& ny<n){if(grid[nx][ny]=='1'){que.push({nx,ny});grid[nx][ny]='0';}}}}}

被围绕区域

130. 被围绕的区域

思路一：利用dfs的visit标识

这里要从边界出发，从四周的O出发，把所有相连的O找到做好标记，这些O是不能被替换成X的。

这里不要回溯，dfs查找出所有值都是所求的

class Solution {
public:void solve(vector<vector<char>>& board) {m = board.size();if (m == 0)return;n = board[0].size();this->board = board;this->visit = vector<vector<bool>>(m, vector<bool>(n, false));// 去边界dfs所有Ofor (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {if (board[i][j] == 'O' && !visit[i][j]) {dfs(i, j);}}}}//内部没有visit标记的O标记成Xfor(int i=1;i<m-1;i++){for(int j=1;j<n-1;j++){if(board[i][j]=='O'&&!visit[i][j]){board[i][j]='X';}}}}private:int m, n;vector<vector<char>> board;vector<vector<bool>> visit;bool isInArea(int x, int y) { return x >= 0 && x < m && y >= 0 && y < n; }int d[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};void dfs(int x, int y) {visit[x][y] = true;for (int i = 0; i < 4; i++) {int nx = x + d[i][0];int ny = y + d[i][1];// 符合条件才dfsif (isInArea(nx, ny) && board[nx][ny] == 'O' && !visit[nx][ny]) {dfs(nx, ny);}}}
};

方法二：直接在棋盘上修改

把所有的边界O标记成A，然后只要是A就还原O，其他还原X

这里一定要棋盘作为一个引用参数

class Solution {
public:void solve(vector<vector<char>>& board) {m = board.size();if (m == 0)return;n = board[0].size();//去边界dfs所有O// 先找两横for (int j = 0; j < n; j++) {dfs(board,0, j);dfs(board,m - 1, j);}// 再找两竖for (int i = 1; i < m - 1; i++) {dfs(board,i, 0);dfs(board,i, n - 1);}// 还原，O还原X，A还原Ofor (int i = 0; i < m; i++) {for (int j = 0; j < n ; j++) {if (board[i][j] == 'O' ) {board[i][j] = 'X';}else if(board[i][j]=='A'){board[i][j]='O';}}}}private:int m, n;bool isInArea(int x, int y) { return x >= 0 && x < m && y >= 0 && y < n; }int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};void dfs(vector<vector<char>>& board,int x, int y) {// 不符合条件returnif (!isInArea(x, y) || board[x][y] != 'O') {return;}//在board做文章board[x][y]='A';for (int i = 0; i < 4; i++) {int nx = x + dx[i];int ny = y + dy[i];dfs(board,nx, ny);}}
};

注意：要么遍历前判断，要么在dfs前有一条不符合题意的return

    // 先找两横for (int j = 0; j < n; j++) {if(board[0][j]=='O')dfs(board,0, j);if(board[m-1][j]=='O')dfs(board,m - 1, j);}// 再找两竖for (int i = 1; i < m - 1; i++) {if(board[i][0]=='O')dfs(board,i, 0);if(board[i][n-1]=='O')dfs(board,i, n - 1);}

void dfs(vector<vector<char>>& board,int x, int y) {// 不符合条件return,针对：for的两个dfsif (board[x][y] != 'O') {return;}board[x][y]='A';for (int i = 0; i < 4; i++) {int nx = x + dx[i];int ny = y + dy[i];if(isInArea(nx,ny)&&board[nx][ny]=='O')dfs(board,nx, ny);}}

因为只有borad[i][j]=='O’才dfs,不然不是的也会被标记成A

如果主程序for提前判断了，就不用dfs不符合return 那个判断了

单词搜索

79. 单词搜索

这里需要用到回溯，因为是找一条路径，参数需要用到index表示当前第i个字符

index的范围是从：0,…,word.size()-1

class Solution {
public:bool exist(vector<vector<char>>& board, string word) {this->m = board.size();if (m == 0)return false;this->n = board[0].size();this->board = board;this->word = word;visit = vector<vector<bool>>(m, vector<bool>(n, false));// 遍历for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (!visit[i][j]) {dfs(i, j, 0);}if (hasword)return true;}}return false;}private:string word;int m, n;vector<vector<char>> board;vector<vector<bool>> visit;bool hasword = false;bool isInArea(int x, int y) { return x >= 0 && x < m && y >= 0 && y < n; }int d[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};void dfs(int x, int y, int index) {if (board[x][y] != word[index])return;if (index == word.size()-1) {hasword = true;return;}for (int i = 0; i < 4; i++) {visit[x][y] = true;int nx = x + d[i][0];int ny = y + d[i][1];if (isInArea(nx, ny) && !visit[nx][ny]) {dfs(nx,ny,index+1);}visit[x][y]=false;}}
};

visit也可以在for外面

        visit[x][y] = true;for (int i = 0; i < 4; i++) {int nx = x + d[i][0];int ny = y + d[i][1];if (isInArea(nx, ny) && !visit[nx][ny]) {dfs(nx,ny,index+1);}}//for的四个方向都不可行，还原该标志visit[x][y]=false;

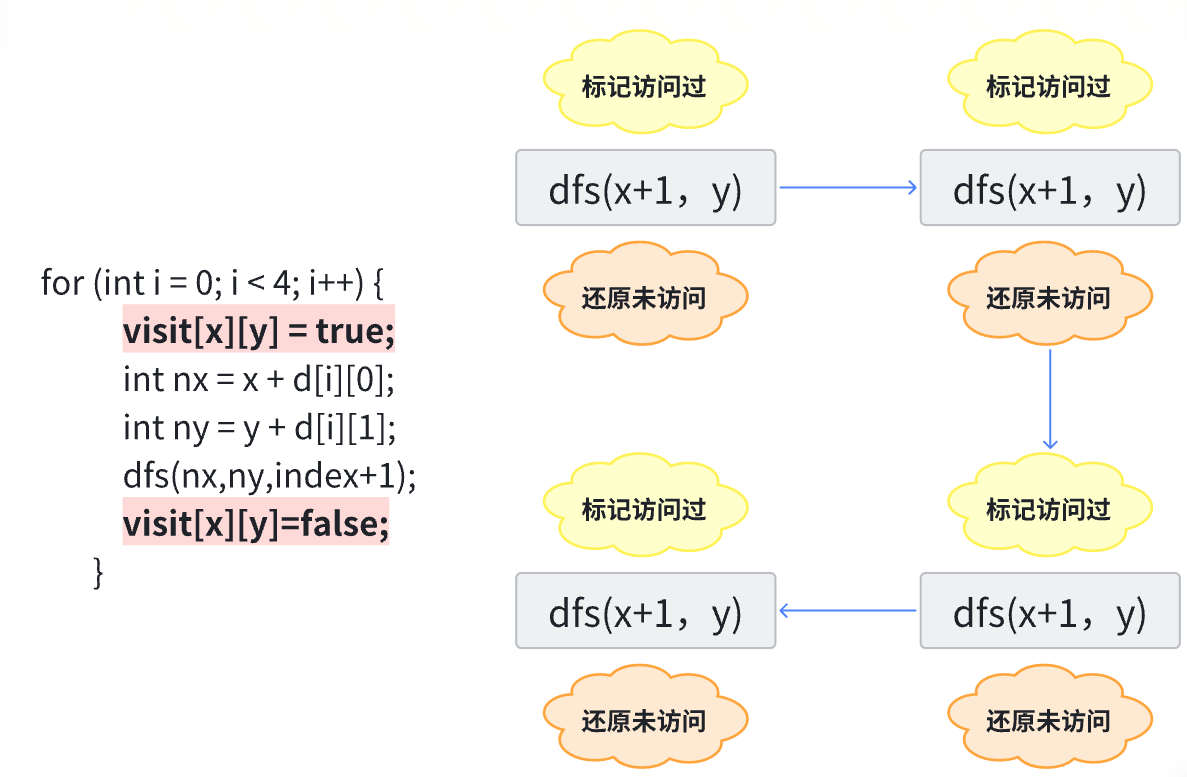
两种标志图示：

最后一个字符满足时候直接判断；

void dfs(int x, int y, int index) {if (index == word.size() - 1 && board[x][y] == word[index]) {hasword = true;return;}//等价于：if (board[x][y] != word[index]){return;}if (board[x][y] == word[index]) {visit[x][y] = true;for (int i = 0; i < 4; i++) {int nx = x + d[i][0];int ny = y + d[i][1];if (isInArea(nx, ny) && !visit[nx][ny]) {dfs(nx, ny, index + 1);}}// for的四个方向都不可行，还原该标志 visit[x][y] = false;}
}

也可以不定义visit,直接让访问的原棋盘数字变成"."

void dfs(int x, int y, int index) {if (board[x][y] != word[index] || board[x][y] == '.')return;// 保证了：board[x][y]==word[index]if (index == word.size() - 1) {hasword = true;return;}char ch = board[x][y];for (int i = 0; i < 4; i++) {board[x][y] = '.';int nx = x + d[i][0];int ny = y + d[i][1];if (isInArea(nx, ny)) {dfs(nx, ny, index + 1);}//board[x][y] = ch;}// 回溯board[x][y] = ch;
}

或者:只要不符合就return

void dfs(int x, int y, int index) {if (!isInArea(x, y) || board[x][y] != word[index] || board[x][y] == '.')return;// 满足条件返回结果if (index == word.size() - 1) {hasword = true;return;}char ch = board[x][y];board[x][y] = '.';for (int i = 0; i < 4; i++) {int nx = x + d[i][0];int ny = y + d[i][1];dfs(nx, ny, index + 1);}// 回溯board[x][y] = ch;
}

五：bfs求最短最长问题

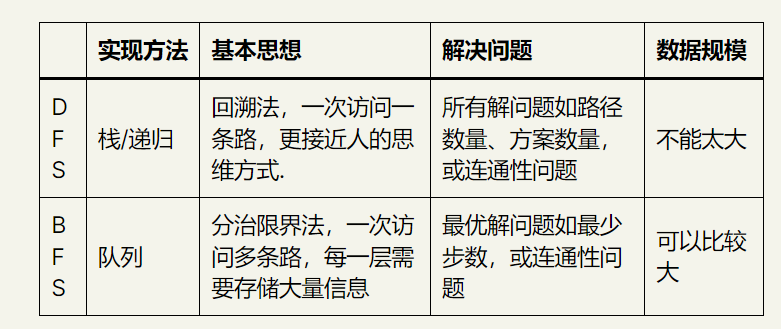
回溯法BFS和分支限界法BFS

最小基因变化

433. 最小基因变化

主要题目中出现最短最长字眼的搜索问题，一般都是用bfs来解决

用map记录字符串，第一次出现的就是最小的，用map存储后，后续不同位置变化出的相同字符串的层数不会更新

用set存储基因库的字符串，便于查找。

 int minMutation(string startGene, string endGene, vector<string>& bank) {//map来记录当前变化的处在哪一层unordered_map<string,int> depth;//st来判断当前string是否在基因库内unordered_set<string> st;for(auto& val:bank) st.insert(val);//队列用来bfsqueue<string> que;que.push(startGene);depth[startGene]=0;//startGene没有变化while(!que.empty()){string tmp=que.front();que.pop();//开始进行8个位置和每个位置3种字符的变化for(int i=0;i<8;i++){for(auto ch:{'A','C','G','T'}){//for(auto ch:"ACGT")//和自己一样的字符不要if(tmp[i]==ch) continue;string next=tmp;next[i]=ch;//next不能重复，而且必须在bank内if(depth.count(next)||!st.count(next)) continue;//更新next的层数,当前根加一depth[next]=depth[tmp]+1;//满足条件返回结果if(next==endGene) return depth[next];//入队que.push(next);}}}//whilereturn -1;}

当然也可以是满足条件执行，而不是不满足条件continue，break或return

                  // next不能重复，而且必须在bank内if (!depth.count(next) && st.count(next)) {depth[next] = depth[tmp] + 1;// 满足条件返回结果if (next == endGene)return depth[next];// 入队que.push(next);}

单词接龙

127. 单词接龙

非常类似最小基因变化，只不过返回的是序列长度，所以mp[begin]=1

在变化上：有字符串长度的位置可选择，每个位置可有26个字母可选

遍历26个小写字母利用ascii码：char ch='a';ch<='z';ch++

  //注意：endword不在wordList必须returnif(!st.count(endWord)) return 0;

class Solution {
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {//定义set记录wordList，快速查找unordered_set<string> st(wordList.begin(),wordList.end());//注意：endword不在wordList必须returnif(!st.count(endWord)) return 0;//定义map记录次数unordered_map<string,int> mp;//返回的是长度，需要算上自己mp.insert({beginWord,1});//mp[beginWord]=1queue<string> que;que.push(beginWord);//队列操作while(!que.empty()){string tmp=que.front();que.pop();int sz=tmp.size();//sz个位置，每个位置25种变化for(int i=0;i<sz;i++){for(char ch='a';ch<='z';ch++){if(tmp[i]==ch) continue;string next=tmp;next[i]=ch;//next必须不在mp中而且在st中//不符合提前returnif(mp.count(next) || !st.count(next)) continue;mp[next]=mp[tmp]+1;//找到返回结果if(next==endWord) return mp[next];que.push(next);}}}return 0;}
}

或者：在找到next就判断

//sz个位置，每个位置25种变化for(int i=0;i<sz;i++){for(char ch='a';ch<='z';ch++){if(tmp[i]==ch) continue;string next=tmp;next[i]=ch;//找到返回结果if(next==endWord) return mp[tmp]+1;//next必须不在mp中而且在st中if(!mp.count(next) &&st.count(next)){mp[next]=mp[tmp]+1;que.push(next);}}}

这篇关于回溯dfs和分支限界bfs的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---