C语言例4-35：鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一。百钱买百鸡、问鸡翁、鸡母和鸡雏各几何？

本文主要是介绍C语言例4-35：鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一。百钱买百鸡、问鸡翁、鸡母和鸡雏各几何？，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

方法一：

代码如下：

//鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一。百钱买百鸡、问鸡翁、鸡母和鸡雏各几何？
//方法一：
#include<stdio.h>
int main(void)
{int x,y,z;for(x=1;x<=20;x++)for(y=1;y<=33;y++)for(z=3;z<=100;z+=3){if((x+y+z==100)&&(5*x+3*y+z/3==100))printf("鸡翁 %d只，鸡母 %d只，鸡雏 %d只\n",x,y,z);}return 0;
}

结果如下：

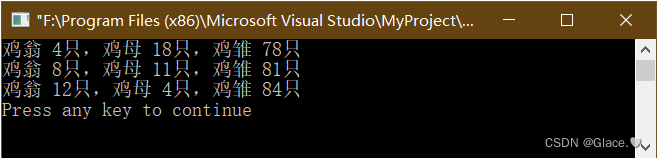
方法二：

算法分析：由于三种鸡的个数之和是固定的，所以需要枚举两种鸡的个数，第三种鸡的个数可以通过判断条件求得，这样三重循环就变成二重循环。

代码如下：

//方法二：
#include<stdio.h>
int main(void)
{int x,y,z;for(x=1;x<=20;x++)for(y=1;y<=33;y++){z=100-x-y;if((z%3==0)&&(5*x+3*y+z/3==100))printf("鸡翁 %d只，鸡母 %d只，鸡雏 %d只\n",x,y,z);}return 0;
}

结果如下：

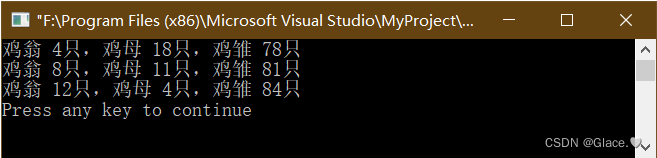
这篇关于C语言例4-35：鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一。百钱买百鸡、问鸡翁、鸡母和鸡雏各几何？的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---