Codeforces Round#768(Div.2) F. Flipping Range

本文主要是介绍Codeforces Round#768(Div.2) F. Flipping Range，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题意：

给定一个数组a，与一个集合B，每次可以选择集合B中的一个元素作为翻转a中一段的大小。使得 $\sum a_{i}$ 最大

题解：

如果我们有x、y∈B（假设x>y），等价于拥有一个x-y大小置入B中，方法是乘以从大小为 x-y 的区间的位置开始的大小为 x 的区间,和一个大小为 y 的区间，结束于与区间 x 相同的位置.或者，将一个大小为 x 的区间与大小为 x−y 的区间在相同位置结束的区间与另一个大小为 y 的区间相乘，该区间的起点与大小为 x 的区间相同。
在这里插入图片描述

对于两个元素 x,y∈B(x>y)，可以将 x−y 添加到 B，重复这样做可以得到 gcd(x,y).
让 g=gcd(b1,b2,…,bm:bi∈B)，通过应用前面的归约 g 是可以得到的最小元素，所有其他元素将是它的倍数。然后问题简化为，将大小为 g 的区间乘以 -1−任意次数，最大化 $\sum a_{i}$

让我们定义大小为 n（0 索引）的字符串 s=000…00，如果第 i 个元素不乘以 -1 ,则si=0，否则 si =1 。该操作翻转大小为 g 的子字符串中的所有 s的值。
让我们将 fx定义为所有 si值的异或，其中 i mod g =x，注意 fx的取值大小为0≤x≤g−1。
在任何操作中，f 的所有值都会同时变化，因为它们在开始时都是 0，只有使所有 fi 相等的 s 的状态是可达的。
证明所有fi相等的s的所有状态都是可达的
让我们从 s的任何状态开始，使得 f=000…00 并重复选择最右边的 i，使得 si=1 和i≥g−1，并翻转以该位置结尾的子字符串，在尽可能多地这样做之后，对于 g−1≤i≤n−1，si=0.对于任何 0≤i<g,si=1.那么 fi=1 这是一个矛盾，因为 fg-1=0并且所有 fi同时变化，则 s=000…00。f 的所有值都等于 1 的情况类似

在此之后，可以使用 dp解决问题。
令dp[i][0]为ai，ai-g,ai-2g,…,ai-kg的最大值，其中：
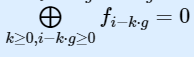
在这里插入图片描述
同理dp[i][1]为：ai-g,ai-2g,…,ai-kg的最大值，其中：

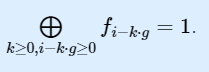
最终答案为：

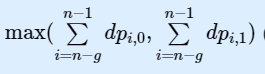
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;int main()
{ios_base::sync_with_stdio(0);cin.tie(0);int T;cin >> T;while(T--){int n,m;cin >> n >> m;vector<int> a(n),b(m);for(int i=0;i<n;i++)cin >> a[i];int g=0;for(int i=0;i<m;i++){cin >> b[i];g=__gcd(g,b[i]);}vector<vector<ll>> dp(g,vector<ll>(2));for(int i=0;i<g;i++)dp[i][1]=-2e9;for(int i=0;i<n;i++){int rem=i%g;ll v0=max(dp[rem][0]+a[i],dp[rem][1]-a[i]);ll v1=max(dp[rem][0]-a[i],dp[rem][1]+a[i]);dp[rem][0]=v0;dp[rem][1]=v1;}ll sum0=0,sum1=0;for(int i=0;i<g;i++){sum0+=dp[i][0];sum1+=dp[i][1];}cout << max(sum0,sum1) << '\n';}return 0;
}