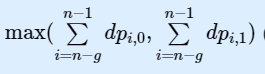768专题
Error:..\FreeRTOS\portable\RVDS\ARM_CM4F\port.c,768
出现这个报错的时候说明:刚刚发生的中断中调用了系统的API函数,但是该中断的优先级超出了系统可管理的优先级范围; 降低该中断的优先级或扩大系统可管理优先级范围即可解决。
【优化调度】基于matlab粒子群算法求解分布式能源调度优化问题【含Matlab源码 768期】
✅博主简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,Matlab项目合作可私信。 🍎个人主页:海神之光 🏆代码获取方式: 海神之光Matlab王者学习之路—代码获取方式 ⛳️座右铭:行百里者,半于九十。 更多Matlab仿真内容点击👇 Matlab图像处理(进阶版) 路径规划(Matlab) 神经网络预测与分类(Matlab) 优化求解(Matlab) 语音处理(Matlab
Codeforces Round#768(Div.2) F. Flipping Range
题意: 给定一个数组a,与一个集合B,每次可以选择集合B中的一个元素作为翻转a中一段的大小。使得 ∑ a i \sum a_{i} ∑ai最大 题解: 如果我们有x、y∈B(假设x>y),等价于拥有一个x-y大小置入B中,方法是乘以从大小为 x-y 的区间的位置开始的大小为 x 的区间,和一个大小为 y 的区间,结束于与区间 x 相同的位置.或者,将一个大小为 x 的区间与大小为 x−y
Codeforces Round#768(Div.2) E. Paint the Middle
题意: 给定编号从 1 到 n的 n 个元素,元素 i 具有值 ai 和颜色 ci,最初,对于所有 i,ci=0。 可以应用以下操作: 选取三个元素i、j、k(1≤i<j<k≤n),使得ci、cj、ck都等于0且ai=ak,则令cj =1。 问 m a x ∑ c i max\sum ci max∑ci为多少 题解: 可以将这题看成区间覆盖的问题,只要两头有个相同的数显然可以将中间所有的ci
Codeforces Round#768(Div.2) C. And Matching
题意: 给定一个值n,表示数组为[0-n-1],其中n一定是2的整数幂,将数字两两配对分别为a[i],b[i],使得 ∑ a i & b i = k \sum a_{i} \&b_{i}=k ∑ai&bi=k, 题解: 1.直接构造出一个答案为k,使得剩下的组合都为0即可。 我们知道: n-1&k=k设c(k)为k的补码, k&c(k)=0 再分情况讨论: Case 0<=k<n−1
【精读】768- 如何更好地理解中间件和洋葱模型
相信用过 Koa、Redux 或 Express 的小伙伴对中间件都不会陌生,特别是在学习 Koa 的过程中,还会接触到 “洋葱模型”。 本文阿宝哥将跟大家一起来学习 Koa 的中间件,不过这里阿宝哥不打算一开始就亮出广为人知的 “洋葱模型图”,而是先来介绍一下 Koa 中的中间件是什么? 一、Koa 中间件 在 @types/koa-compose 包下的 index.d.ts 头文件中我们
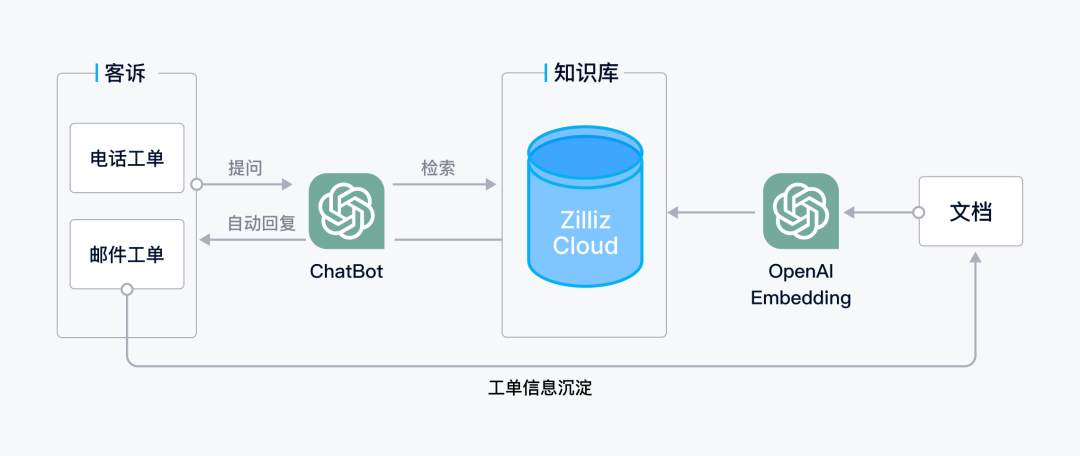
客户案例|100M 768 维向量数据,Zilliz Cloud 稳定支持 Shulex VOC 业
日前,国际化 VOC SaaS 公司数里行间(Shulex)将上亿数据量的核心业务从开源向量数据库 Milvus 迁移至全托管的向量数据库云服务 Zilliz Cloud。 相比于 Milvus,Zilliz Cloud 实现了 Shulex VOC 评论分析洞察报告生成速度 30% 的提升,VOC 智能客服召回率 98%,且系统稳定,0 宕机,大大降低了企业在向量数据库的运维成本。 01
openssl3.2/test/certs - 010 - 768-bit key
文章目录 openssl3.2/test/certs - 010 - 768-bit key概述笔记END openssl3.2/test/certs - 010 - 768-bit key 概述 openssl3.2 - 官方demo学习 - test - certs 笔记 // \file my_openssl_linux_log_doc_010.txt // \no
Codeforces Round 768 (Div. 1) D. Flipping Range(思维题 等价类性质 dp)
题目 思路来源 官方题解 洛谷题解 题解 可操作的最短区间长度肯定是gcd,记为g,然后考虑如何dp 考虑g个等价类,每个等价类i,i+g,i+2*g,... 每次翻转长度为g的区间,会同时影响到g个等价类总的翻转的奇偶性, 性质一:只有每个等价类翻的次数奇偶性相同才合法 性质二:此外,翻1-g和翻2-g+1可以起到翻(1,g+1)效果 等价类内翻两个相邻的,可以类似
【教学类-43-13】 20240103 (4宫格数独:错误版:768套) 不重复的基础模板数量:768套
作品展示:——4宫格 768套不重复模板(64页*12套题) 有错误,实际数量小于768套 背景需求: 测试4宫格数独基础模板有几种。 写个程序,验算是不是真的是乘阶法的288种。 代码展示: 768套4宫格题目不重复,每页12套=64页 # 测试11*11格,2*2一共4套3*3 宫格'''目的:数独14 4宫格有758套不同的基础模板作者:阿夏时间:
计算机组成原理像素为768,【计算机组成原理】输入输出系统(一)
I/O分类: I/O设备通过设备控制器与主板的系统总线相连。 I/O程序查询方式: 1、程序查询方式 程序查询方式、程序中断方式用于速度较低的外设。 DMA和通道方式用于速度较高的外设。 浮点数下溢当机器0处理,不需要中断处理,浮点数上溢,需要中断处理 只有具有DMA接口的设备才能产生DMA请求 程序查询方式中,COU与外设串行工作,传送与主程序串行工作 中断方式CPU与外设并行,数据准备
LeetCode 768. 最多能完成排序的块 II(java)
1.问题 给定数组中的元素可以重复,输入数组最大长度为2000,其中的元素最大为10**8。 arr是一个可能包含重复元素的整数数组,我们将这个数组分割成几个“块”,并将这些块分别进行排序。之后再连接起来,使得连接的结果和按升序排序后的原数组相同。 我们最多能将数组分成多少块? 原题链接; 2.解法 class Solution {public int maxChunksToSort