本文主要是介绍状态压缩DP【蒙德里安的梦想】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目描述

输入样例
1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0
输出样例
1
0
1
2
3
5
144
51205
题目链接
https://www.acwing.com/problem/content/293/
分析
- 总方案数即为横放的方案数,因为横放完后列填补只会出现一种情况
1表示横放,0表示竖放- 如果合并列不存在
连续的奇数个``0,即为合法状态(偶数个的话可以竖放填补) - 初始时
f[0,0]表示第0行不横放合法,故值为1 - 每一个状态由上一列递推累加方案数和而来
- 目标:
f[m][0],已经摆放完m列,且不会向下一行伸出
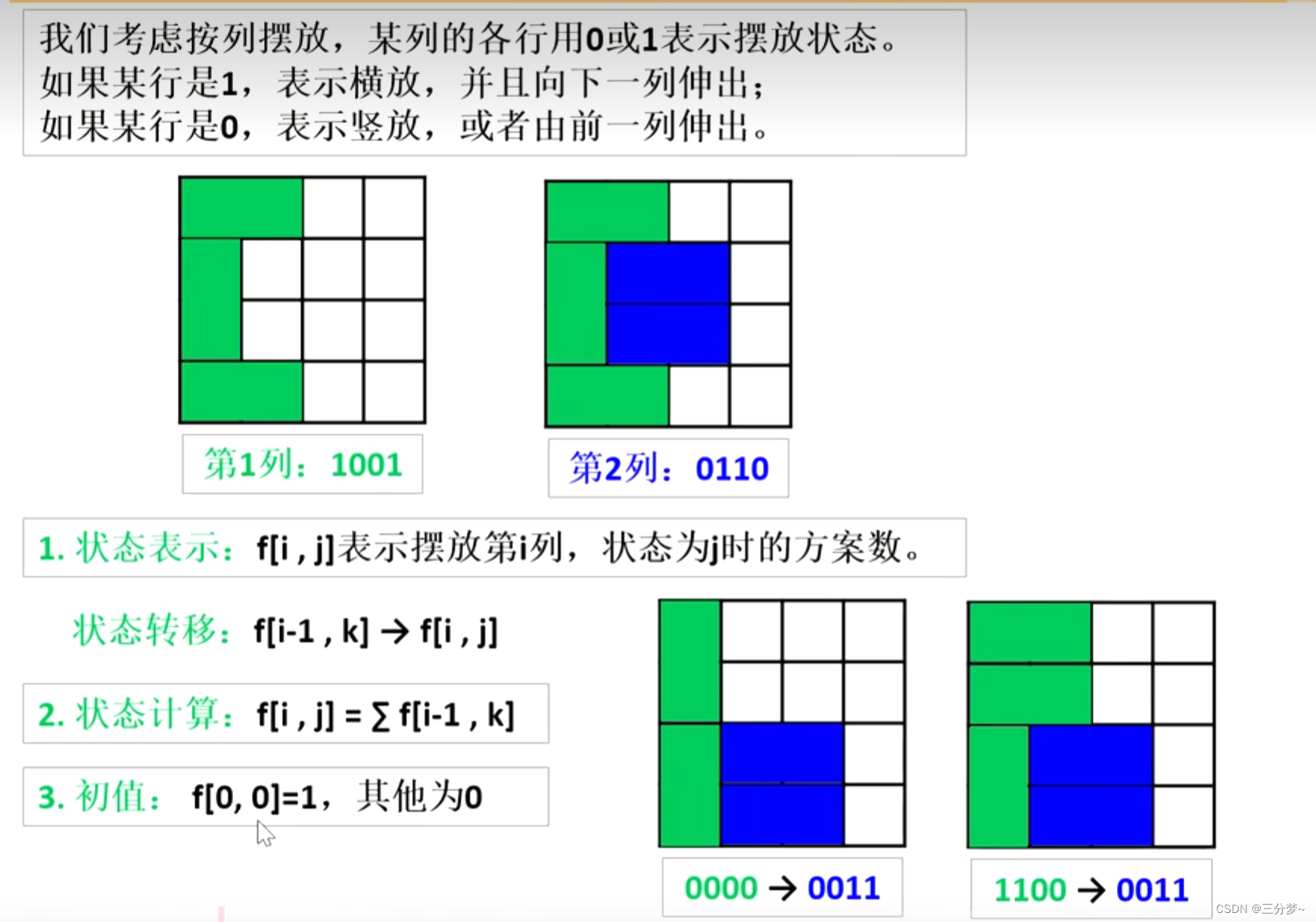
预处理:判断是否合法

具体注释及代码见下方
【AC代码】
#include<iostream>
#include<cstring>using namespace std;//数据范围1~11
const int N = 12;
//每一列的每一个空格有两种选择,放和不放,所以是2^n
const int M = 1 << N;
//方案数比较大,所以要使用long long 类型
//f[i][j]表示 i-1列的方案数已经确定,从i-1列伸出,并且第i列的状态是j的所有方案数
long long f[N][M];
//第 i-2 列伸到 i-1 列的状态为 k , 是否能成功转移到 第 i-1 列伸到 i 列的状态为 j
//st[j|k]=true 表示能成功转移
bool st[M]; //判断空着的长度是否为偶数,是否可以填满
//n行m列
int n, m;int main() {
// 预处理st数组while (cin >> n >> m, n || m) {for (int i = 0; i < 1 << n; i++) {
// 第 i-2 列伸到 i-1 列的状态为 k ,
// 能成功转移到
// 第 i-1 列伸到 i 列的状态为 jst[i] = true;
// 记录合并列中连续的0的个数int cnt = 0;for (int j = 0; j < n; j++) {
// 通过位操作,i状态下j行是否放置方格,
// 0就是不放, 1就是放if (i >> j & 1) {
// 如果放置小方块使得连续的0个数成为奇数,
// 这样的状态就是不行的,if (cnt & 1) {st[i] = false;break;}}else cnt++;
// //不放置,则0的个数++}if (cnt & 1) st[i] = false; //对高位0的处理,比如0100不合法}// 初始化状态数组fmemset(f, 0, sizeof f);// 棋盘是从第0列开始,没有-1列,所以第0列第0行,不会有延伸出来的小方块
// 没有横着摆放的小方块,所有小方块都是竖着摆放的,这种状态记录为一种方案f[0][0] = 1;
// 遍历每一列for (int i = 1; i <= m; i++) {
// 枚举i列每一种状态for (int j = 0; j < 1 << n; j++) {
// 枚举i-1列每一种状态for (int k = 0; k < 1 << n; k++) {
// f[i-1][k] 成功转到 f[i][j]if ((j & k) == 0 && st[j | k]) {f[i][j] += f[i - 1][k]; //那么这种状态下它的方案数等于之前每种k状态数目的和}}}}
// 棋盘一共有0~m-1列
// f[i][j]表示 前i-1列的方案数已经确定,从i-1列伸出,并且第i列的状态是j的所有方案数
// f[m][0]表示 前m-1列的方案数已经确定,从m-1列伸出,并且第m列的状态是0的所有方案数
// 也就是m列不放小方格,前m-1列已经完全摆放好并且不伸出来的状态cout << f[m][0] << endl;}return 0;
}这篇关于状态压缩DP【蒙德里安的梦想】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





