【OJ】动归练习四

本文主要是介绍【OJ】动归练习四，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

个人主页 ： zxctscl
如有转载请先通知

1. 面试题 17.16. 按摩师

1.1 分析

1. 状态表示
   以i位置为结尾总的分钟数最长，这里要考虑，要不要选择i位置的值。
   就分两种情况，如果选择了i位置那么就记为f[i]；
   如果没有选择i位置的值就记为g[i]。

2. 状态转移方程
   要考虑到达i位置时候，这个位置选择了就得加上这个位置对应的值nums[i]，那么它前面的位置i-1就不能选择，这个时候的状态转移方程就是f[i]=g[i-1]+nums[i];
   如果不选择这个位置，那么它前面的位置i-1也可以选也可以不选，如果选就是f[i-1],如果不选择就是g[i-1]，比较一下取大的一个就行，这个时候的状态转移方程就是g[i]=max(f[i-1],g[i-1])。

3. 初始化
   得考虑第一个位置，如果选择，那么就是这个位置对应的值f[0]=nums[0]；如果不选择，那么这个位置的值就是0：g[0]=0。
   如果给的数据为空，就直接返回0。

4. 填表顺序
   从左往右

5. 返回值
   按题目要求返回最后一个位置最长时间就行，取两种选择中大的那个max(f[n-1],g[n-1])。
   

1.2 代码

class Solution {
public:int massage(vector<int>& nums) {int n=nums.size();if(n==0)return 0;vector<int> f(n);auto g=f;f[0]=nums[0];g[0]=0;for(int i=1;i<n;i++){f[i]=g[i-1]+nums[i];g[i]=max(f[i-1],g[i-1]);}return max(f[n-1],g[n-1]);}
};

2. 198. 打家劫舍

2.1 分析

这个题目和上面那个题分析一模一样

2.2 代码

class Solution {
public:int massage(vector<int>& nums) {int n=nums.size();if(n==0)return 0;vector<int> f(n);auto g=f;f[0]=nums[0];g[0]=0;for(int i=1;i<n;i++){f[i]=g[i-1]+nums[i];g[i]=max(f[i-1],g[i-1]);}return max(f[n-1],g[n-1]);}
};

3. 213.打家劫舍 II

3.1 分析

题目与上面一个题不同的是，这里首位是相连的，而相连的不可以偷。

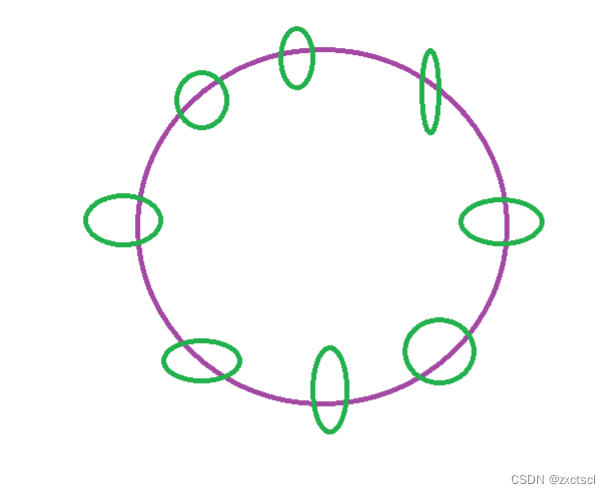
那么就转换为两个像打家劫舍的问题。
有两种情况：一、偷第一个位置，那么n-1位置就不能偷，那么2到n-2，就可以像打家劫舍那样偷。二、不偷第一个位置，那么n-1位置就偷，那么1到n-1位置就可以像打家劫舍那样偷。
所以这里就通过分类将环形问题，转换为上面两个线性的打家劫舍问题。

1. 状态表示
   以i位置为结尾总的金额最和大，这里要考虑，要不要选择i位置的值。
   就分两种情况，如果选择了i位置那么就记为f[i]，还得加上这个位置对应的值nums[i]，就是此时的最大金额；
   如果没有选择i位置的值就记为g[i]，表示此时的最大金额。

2. 状态转移方程
   要考虑到达i位置时候，这个位置选择了就得加上这个位置对应的值nums[i]，那么它前面的位置i-1就不能选择，这个时候的状态转移方程就是f[i]=g[i-1]+nums[i];
   如果不选择这个位置，那么它前面的位置i-1也可以选也可以不选，如果选就是f[i-1],如果不选择就是g[i-1]，比较一下取大的一个就行，这个时候的状态转移方程就是g[i]=max(f[i-1],g[i-1])。

3. 初始化
   得考虑第一个位置，如果选择，那么就是这个位置对应的值f[0]=nums[0]；如果不选择，那么这个位置的值就是0：g[0]=0。
   如果给的数据为空，就直接返回0。

4. 填表顺序
   从左往右

5. 返回值
   代码就直接写一个打家劫舍的函数，返回出两种分类结果的值，比较两次打家劫舍的返回值，返回大的值return max(nums[0]+rob1(nums,2,n-2),rob1(nums,1,n-1));

3.2 代码

class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();if (n == 0)return 0;return max(nums[0]+rob1(nums,2,n-2),rob1(nums,1,n-1));     }int rob1(vector<int>& nums,int left,int right){if(left>right)return 0;int n = nums.size();vector<int> f(n);auto g = f;f[left] = nums[left];for (int i = left; i <=right; i++) {f[i] = g[i - 1] + nums[i];g[i] = max(f[i - 1], g[i - 1]);}return max(f[right], g[right]);}};

有问题请指出，大家一起进步！！！

这篇关于【OJ】动归练习四的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---