802 找到最终的安全状态

本文主要是介绍802 找到最终的安全状态，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目

有一个有 n 个节点的有向图，节点按 0 到 n - 1 编号。图由一个 索引从 0 开始 的 2D 整数数组 graph表示， graph[i]是与节点 i 相邻的节点的整数数组，这意味着从节点 i 到 graph[i]中的每个节点都有一条边。

如果一个节点没有连出的有向边，则该节点是 终端节点 。如果从该节点开始的所有可能路径都通向 终端节点 ，则该节点为 安全节点 。

返回一个由图中所有 安全节点 组成的数组作为答案。答案数组中的元素应当按升序排列。

示例 1：

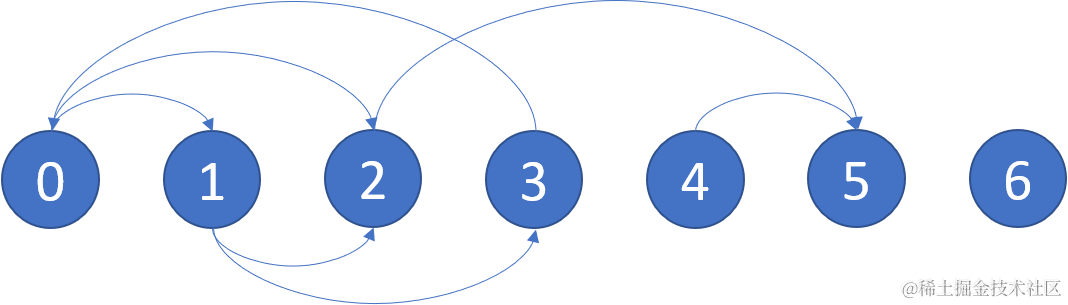
Illustration of graph

输入： graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出： [2,4,5,6]
解释： 示意图如上。
节点 5 和节点 6 是终端节点，因为它们都没有出边。
从节点 2、4、5 和 6 开始的所有路径都指向节点 5 或 6 。

解法

这道题的本质究其根本就是寻找有无环路，如果一道题目需要检测图中是否存在环路，算法如下：

深度优先搜索（DFS） ：通过深度优先搜索遍历图的所有节点，并标记节点状态，如果在搜索过程中发现某个节点已经被访问过且还未完成遍历，则存在环路。
广度优先搜索（BFS） ：通过广度优先搜索遍历图的所有节点，并检测是否存在环路。
拓扑排序：拓扑排序是一种特殊的排序算法，它可以对有向无环图进行排序，如果图中存在环路，则无法进行拓扑排序。
并查集：并查集也可以用于检测图中是否存在环路，特别适用于无向图

BFS + 拓扑序列 + 逆转图

class Solution {int N = 100010, M = N * 2 + 10, idx = 0;int[] ne = new int[M], e = new int[M], h = new int[N], cnt = new int[N];public void add(int a, int b) {e[idx] = b;ne[idx] = h[a];h[a] = idx ++;}public List<Integer> eventualSafeNodes(int[][] graph) {// 首先想到的是拓扑序列，因为终端节点意味着没有出度，// 能所有边都到达终端节点的即为安全节点，所以可以想逆转图，即出度和入度转换Arrays.fill(h, -1);int n = graph.length;for(int i = 0;i < n;i ++) {for(int j : graph[i]) {add(j, i); // 转换出度入度cnt[i] ++;}}Deque<Integer> de = new ArrayDeque<>();  // 注意这个双向队列for(int i = 0;i < n;i ++) {if(cnt[i] == 0) {de.addFirst(i);}}while(!de.isEmpty()) {int t = de.pollLast();for(int i = h[t];i != -1;i = ne[i]) {int j = e[i];cnt[j] --;if(cnt[j] == 0) {de.addFirst(j);}}}ArrayList<Integer> ans = new ArrayList<>();for(int i = 0;i < n;i ++) {if(cnt[i] == 0) {ans.add(i);}}return ans;}
}

三色图

class Solution {// 三色标记法，0 --- 未被访问过， 1 --- 正在访问中， 2 --- 已经访问过public List<Integer> eventualSafeNodes(int[][] graph) {int n = graph.length; int[] color = new int[n];List<Integer> ans = new ArrayList<Integer>();for(int i = 0;i < n;i ++) {if(isSafe(graph, color, i)) {ans.add(i);}}return ans;}public boolean isSafe(int[][] graph, int[] color, int x) {if(color[x] != 0) {return color[x] == 2;}color[x] = 1;for(int y : graph[x]) {if(!isSafe(graph, color, y)) {return false;}}color[x] = 2;return true;}
}