超大规模集成电路设计----基于阵列的可编程逻辑（七）

本文仅供学习，不作任何商业用途，严禁转载。本篇文章绝大部分资料来自中国科学院段成华教授PPT

超大规模集成电路设计----基于阵列的可编程逻辑（七）

• 7.1 引言
• • 7.1.1.回顾
  • 7.1.2. 数字逻辑系列Digital Logic Families
  • 7.1.3.从定制到半定制和结构化阵列设计方法
• 7.2 可编程阵列逻辑Programmable Array Logic(PAL)
• • 7.2.1 PAL Concept
  • 7.2.2 Basic PAL Array Architecture
  • 7.2.3 PAL Output Structures
  • 7.2.4 使用PALs设计示例
• 7.3 通用阵列逻辑Generic Array Logic
• • 7.3.1 GAL Architecture
  • 7.3.2 OLMC: Output Logic Macro Cell
  • • 7.3.3 GAL Design Example
• 7.4 复杂可编程逻辑器件Complex Programmable Logic Devices (CPLD)
• • 7.4.1 引言
  • • 7.4.1.1 CPLD Architectures
  • 7.4.2 XPLA3 CPLD Architecture
  • • 7.4.2.1 ==Architecture==
    • 7.4.2.2 ==Interconnect Matrix - ZIA==
    • • 7.4.2.2.1交叉点开关Crosspoint Switch
      • 7.4.2.2.2 2:1Mux Based Interconnect
      • 7.4.2.2.3 XPLA3 ZIA
    • 7.4.3 Logic Block
    • 7.4.3.1 Variable Function Mux (VFM)
    • 7.4.3.2 Fold-back NANDs
  • 7.4.4 Fold-back PAL versus PLA
  • 7.4.5 Product Term Sharing
  • 7.4.6 PTs Allocation Techniques
  • 7.4.7 ==宏单元Macrocell(MC) 重点==
  • • 总体描述（重点）
    • 寄存器功能
    • 时钟
    • 输入时寄存器配置方式
    • 补充：埋在逻辑块中且未连接到I/O的宏单元与非埋入的宏单元的区别
    • I/O单元
• 7.5 FPGA-Field Programmable Gate Arrays
• • • 7.5.1FPGA制作工艺
    • • 反熔丝Anti-fuse (non-volatile)
      • SRAM
      • EPROM 和 E²PROM
      • Flash
    • 7.5.2 FPGA的结构
  • 7.5.3 布尔方程和逻辑生成器
  • • 7.5.3.1 布尔方程
    • • 1. 最小项Min-Term
      • 2. 正则表达式Canonical expressions
      • 3.香浓扩展定理Shannon’s expansion theorem
      • 4. 正则定理Canonical theorem
    • 7.5.3.2 逻辑生成器
    • • 1. 基于PT原理
      • ==2. 基于MUX原理==
      • ==3. 基于LUT原理==
  • 7.5.4Configurable Logic Blocks
  • • 7.5.4.1. ACT Logic Modules
    • 7.5.4.2 XC 3000 CLB
    • • Combinational Logic Options:
    • 7.5.4.3 XC4000 CLB
    • • 1. 把XC4000 的逻辑生成器当RAM用
      • • 1. 16x2 (or 16x1) Edge-Triggered Single-Port RAM
        • 2. 32x1 Edge-Triggered Single-Port RAM (F and G addresses are identical）
        • 3. Dual-Port RAM, Simple Model
      • 2. XC4000 中的超前进位链
  • 7.5.5 可编程I/O
  • • 7.5.5.1 三态门
    • 7.5.5.2 XC3000 I/O
    • 7.5.5.3 XC4000 I/O
• 7.6 亚稳态Metastability

为什么要学习这一章：这一章详细地介绍了PAL、GAL、CPLD、FPGA等可编程逻辑器件，以及浅析了亚稳态。CPLD和FPGA部分需要重点学习，前面GAL和PAL可以粗略的看。标黄部分属于必须掌握的部分，黑体部分表示强调部分，有助于理解，对于普通字体部分，时间紧急的浏览者可以选择忽略，对于初学者，建议博文每部分都需要连贯阅读。

7.1 引言

7.1.1.回顾

纯定制设计是 1970 年代早期集成电路的常态。
1980s ~:
◆ Programmable logic array (PLAs),
◆ Standard cells,
◆ Macrocells,
◆ Module compilers,
◆ Gate arrays,
◆ Reconfigurable hardware

7.1.2. 数字逻辑系列Digital Logic Families

Standard products (Dedicated General Purpose Devices)
TTL, HC, HCT, 4000/4500
✓ Programmable logic
PAL, GAL, PROM/FLASH, CPLD, FPGA
✓ Custom logic
Full-custom: Handcrafted designs
Semi-custom: Gate Arrays, Standard cells, Macrocells, SoC/NoC

7.1.3.从定制到半定制和结构化阵列设计方法

From Custom to semicustom and Structured-Array Design Approaches

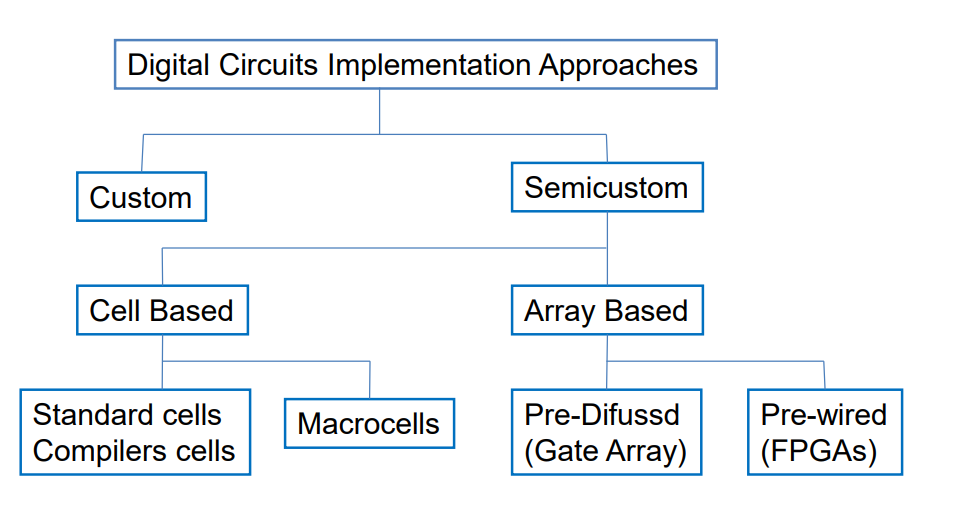
Examples of full custom cell and semicustom cell:

7.2 可编程阵列逻辑Programmable Array Logic(PAL)

7.2.1 PAL Concept

特点：
i. PAL/GAL, PROM, PLA devices share the same internal AND-OR structure,PAL/GAL、PROM、PLA 器件具有相同的内部 AND-OR 结构
ii. Varying allocation of logic features and amount of programmability.不同的逻辑功能分配和可编程性。
iii. Two levels of function: AND and OR array.两个级别的函数：AND 和 OR 数组。
iv. Implementing logic in the form of Boolean sum-of-products.以布尔乘积和的形式实现逻辑

7.2.2 Basic PAL Array Architecture

特点

1. AND array is programmable;
2. OR array is fixed;
   3.== Two AND-gates are dedicated to each OR-gate.每个或门都连接着两个与门==

7.2.3 PAL Output Structures

1. 高电平有效双向输出Active HIGH Bidirectional Output

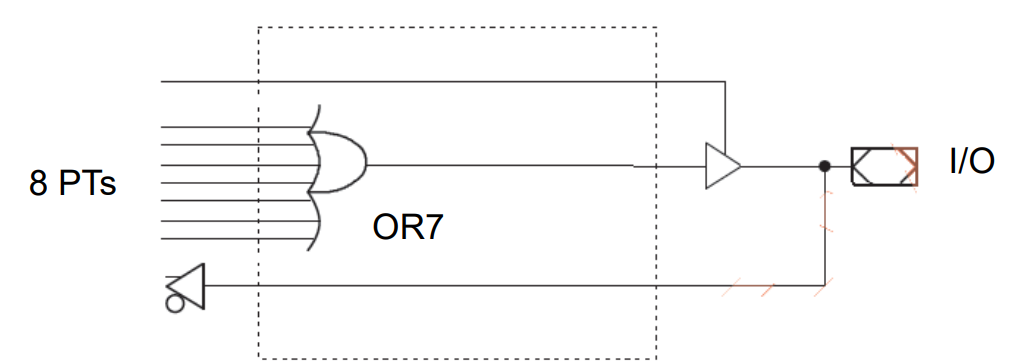
特点
◼ ==Programmable outputs enable as a function of an AND-gate in the array.可编程输出使能是阵列中与门的函数。简单说就是一个与门控制着上图中三态门的输出
◼ Output buffer programmed in three ways:
• As a dedicated output,
•A dedicated input, and
•A dynamically controllable input/output.动态可控的输入/输出。简单说就是输入输出可配置
◼ Feedback path allows more complex logic functions to be implemented 反馈路径允许实现更复杂的逻辑功能 简单说就是允许输出反馈回来再构成逻辑

2. 低电平有效双向输出Active LOW Bidirectional Output
   

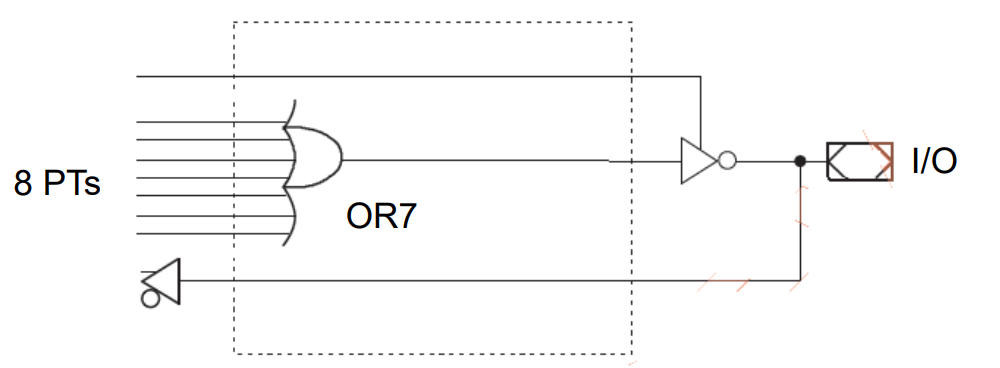
3. 低电平有效XOR双向输出Active LOW XOR Bidirectional Output
   

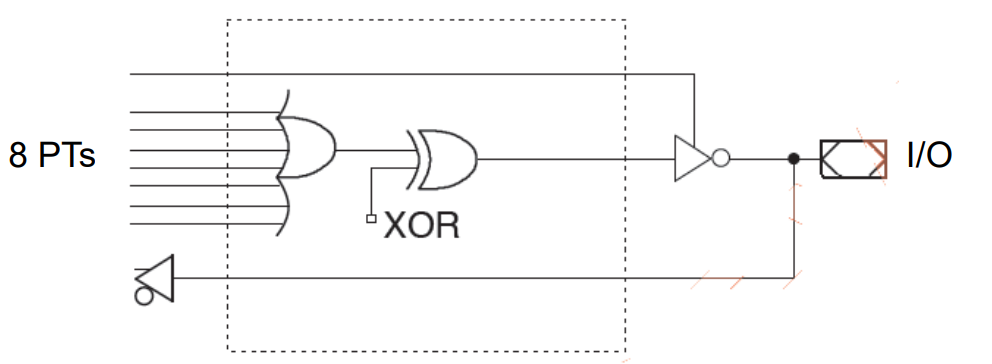
4. 异或寄存输出XOR Registered Output
   
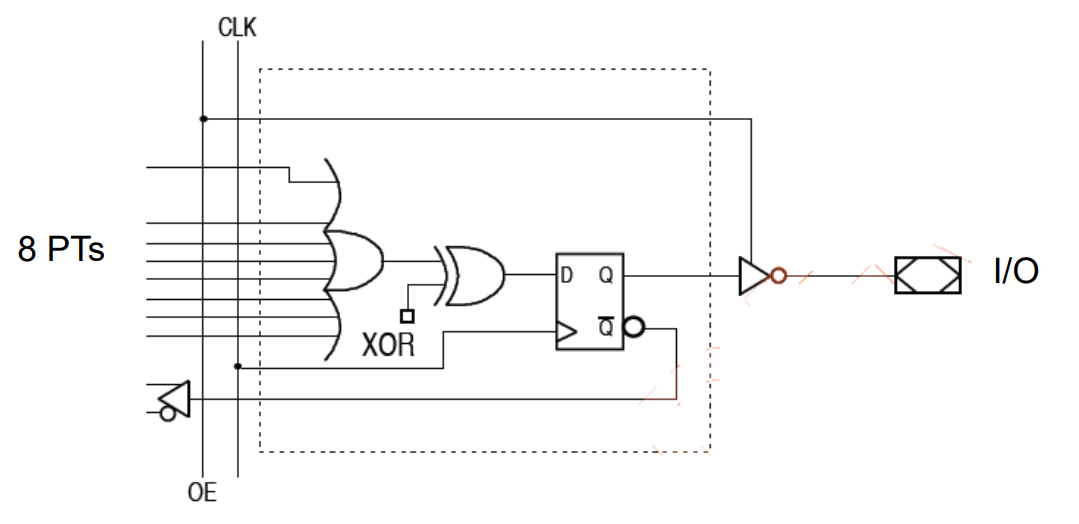
   特点
   ◼ Simplifying state machine design.
   ◼ Placed on data bus.
   ◼ CLOCK and Output Enable are dedicated.

7.2.4 使用PALs设计示例

1. 基本逻辑门的设计
   $\begin{array}{rl}& B=\overline{A},\\ & E=C\cdot D,\\ & H=F+G,\\ & O=\overline{M+N},\\ & R=P\cdot \overline{O}+\overline{P}\cdot O,\\ & L=\overline{I\cdot J\cdot K}\end{array}$

设计规范Design specification:

2. 内存映射 I/O

7.3 通用阵列逻辑Generic Array Logic

7.3.1 GAL Architecture

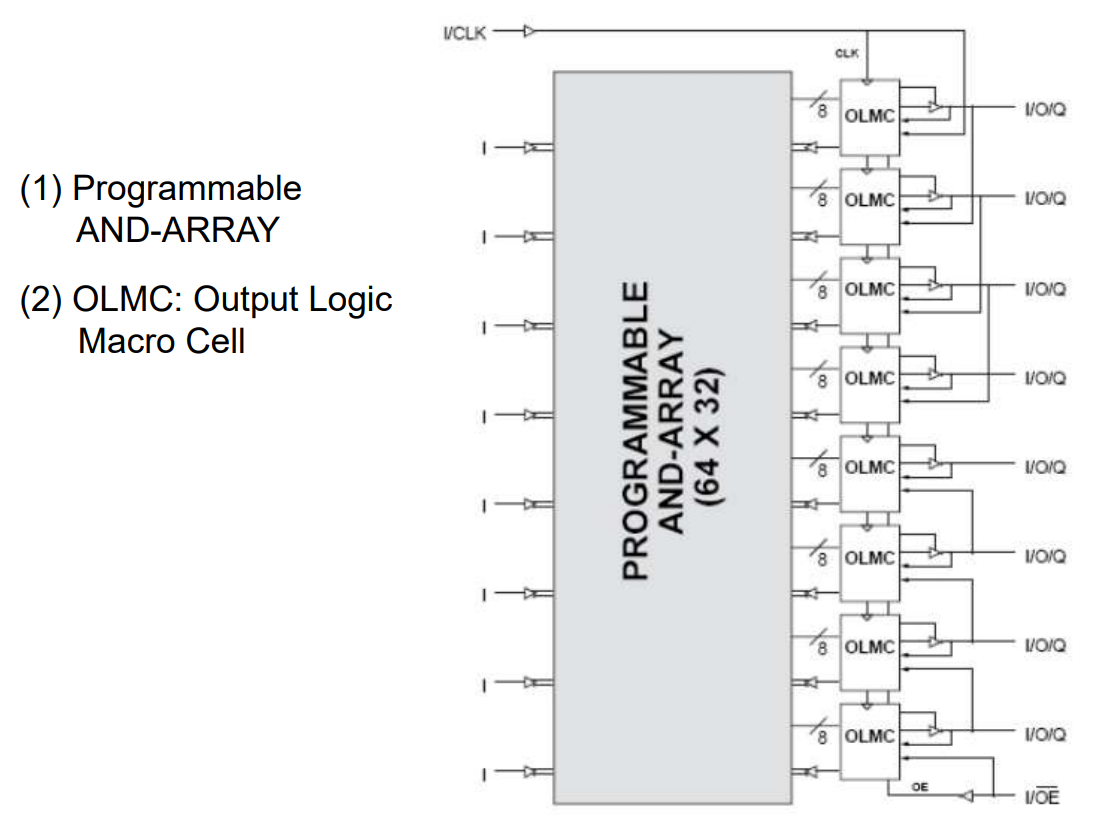
7.3.2 OLMC: Output Logic Macro Cell

PMUX: Path multiplexer TMUX: 3-state mux
OMUX: Output mux FMUX: Feedback mux

7.3.3 GAL Design Example

Implement SN374 8-bit FFs.

7.4 复杂可编程逻辑器件Complex Programmable Logic Devices (CPLD)

7.4.1 引言

7.4.1.1 CPLD Architectures

(1) Xilinx XPLA3 Architecture
(2) XC9500 Architecture

7.4.2 XPLA3 CPLD Architecture

7.4.2.1 Architecture

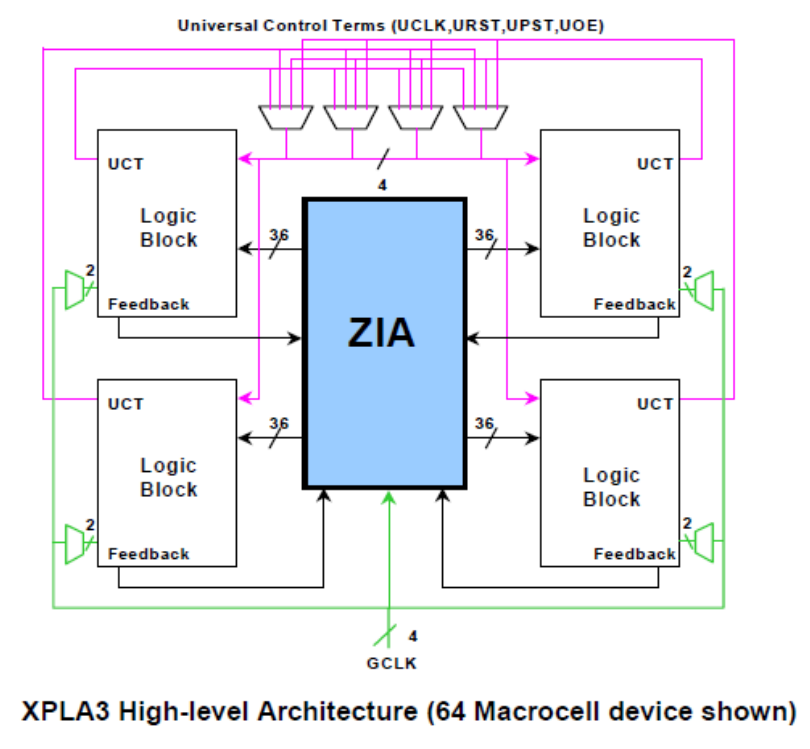
◆ ==A 4-bit Universal Bus is used to provide
✓ an individual asynchronous clock (UCLK),
✓ reset (URST),
✓ preset (UPST), and
✓ output enable (UOE). ==
◆ These bus lines are driven by four multiplexers (muxes), with the mux inputs consisting of a single control p-term from each Logic Block. 这些总线由四个多路复用器（多路复用器）驱动，多路复用器输入由来自每个逻辑块的单个control p-term组成。

7.4.2.2 Interconnect Matrix - ZIA

The routing matrix is called the ZIA (Zero-power Interconnect Array)，当然也只是号称无功耗，其实还是有功耗的
The interconnect resource is supposed to act like a crosspoint switch to route signals from(互连资源应该像交叉点开关一样路由信号)
✓ Inputs to function blocks,
✓ I/Os, and
✓ macrocell feedbacks to the logic blocks

7.4.2.2.1交叉点开关Crosspoint Switch

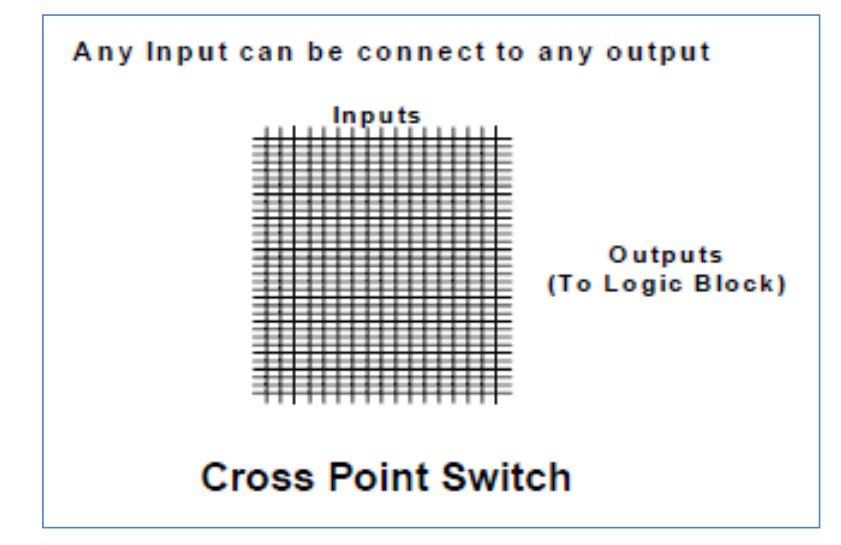
特点
✓ Any input can be connected to any output.任何输入都可以连接到任何输出。
✓ A typical 128 macrocells device would need 65536 (256X256) connections.典型的 128 宏单元设备需要 65536 （256X256） 个连接。
✓ Relative slow (8 – 15 ns delay).相对较慢（8 – 15 ns 延迟）。

7.4.2.2.2 2:1Mux Based Interconnect

7.4.2.2.3 XPLA3 ZIA

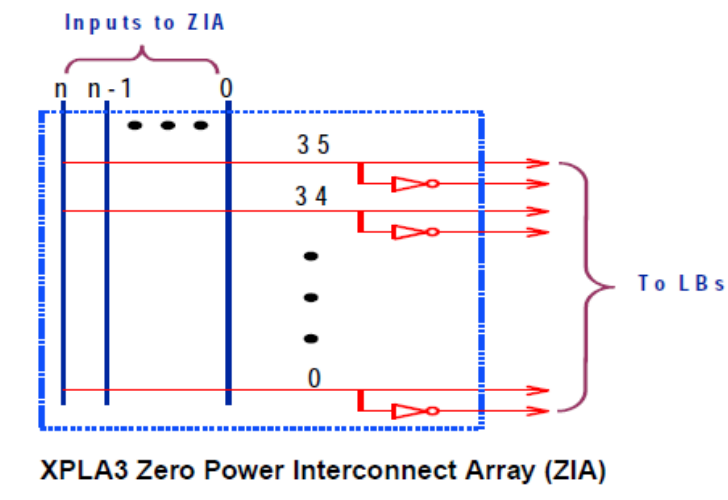
• The interconnect employs a sufficiently large number of input muxes, of sufficient width 互连采用足够多的输入多路复用器，具有足够的宽度。
• Signal routing of 99.997% when every I/O, input pin, and macrocell is in use and has a fixed pinout.

7.4.3 Logic Block

7.4.3.1 Variable Function Mux (VFM)

利用PT项和MUX生成函数

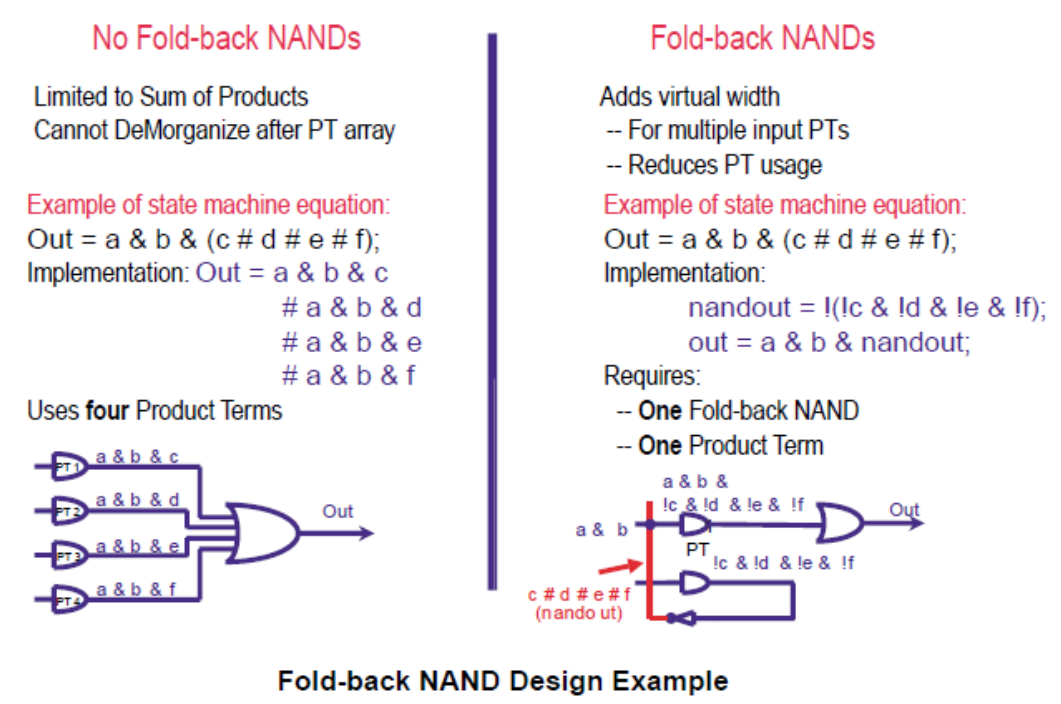
7.4.3.2 Fold-back NANDs

==折叠门，生成非逻辑再反馈回去。==下面是折叠门的例子。

7.4.4 Fold-back PAL versus PLA

PAL注重逻辑电路，PLA注重阵列，PAL的与门可编程或门固定，PLA的与门或门均可编程

7.4.5 Product Term Sharing

PLA的乘积项是能给多个或门用的。

7.4.6 PTs Allocation Techniques

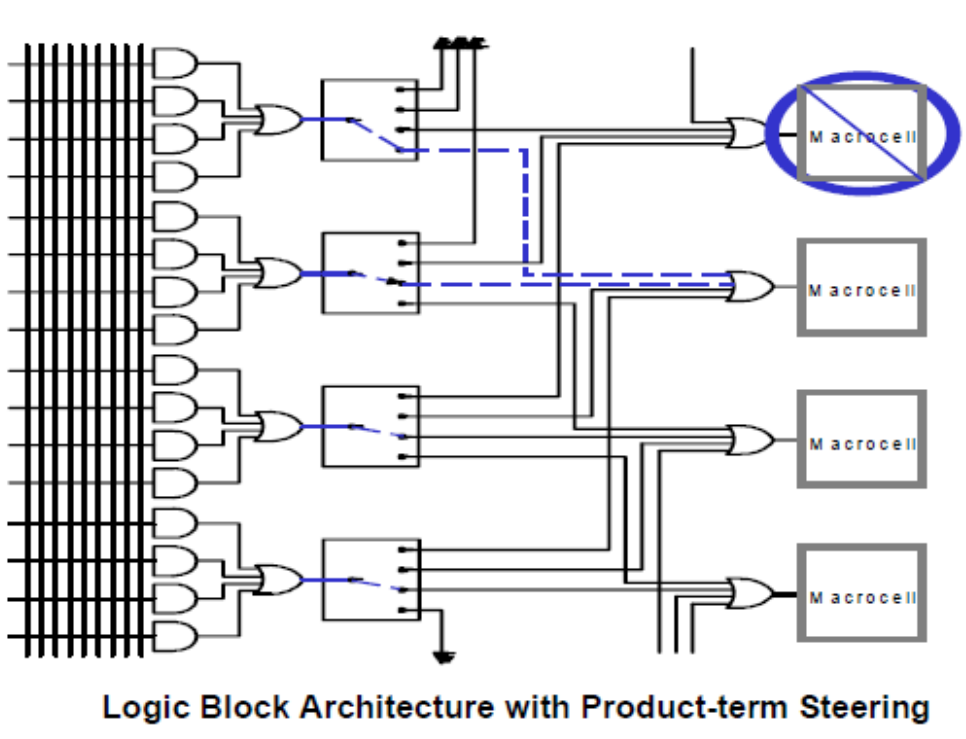
乘积项能给多个宏单元使用

7.4.7 宏单元Macrocell(MC) 重点

总体描述（重点）

如图所示，每个宏单元都可以支持组合或寄存器输入、每个宏单元的通用置位和复位以及可配置的 D、T 或 L 寄存器，具有最大的时钟灵活性。ZIA 有两条反馈路径：一条来自宏单元，另一条来自 I/O 引脚。当 I/O 用作输出时，输出缓冲区被启用，并且宏单元反馈路径可用于反馈宏单元中实现的逻辑。 当 I/O 引脚用作输入时，输出缓冲器将处于高阻状态，输入信号将通过 I/O 反馈路径馈入 ZIA。在VFM中实现的逻辑可以通过宏单元反馈路径反馈给 ZIA系统。埋在逻辑块中且未连接到 I/O 的宏单元与非埋入的宏单元相同。每个宏单元都可用于实现寄存功能或组合功能。

寄存器功能

每个宏单元寄存器的数据输入来自可变函数多路复用器的输出。每个宏单元寄存器可配置为 D、T 或锁存器型触发器;该触发器也可以配置为输入寄存器。每个触发器都具有异步置位和复位功能。有七种不同的置位和复位源：一个通用控制项（ [UCT1]用于置位，[UCT2]用于复位 ）和六个共享的本地控制项 （LCT[0-5]）。

时钟

每个宏单元的寄存器都可以从八个信号源中的任何一个时钟进行驱动。哪八个呢？看下面。==

1. 有两个全局时钟，这两个全局时钟是通过一个 4：2 多路复用器从四个外部时钟引脚产生。
2. 有一个通用时钟信号 （UCT0） 由通用控制项提供。
3. 有四个本地控制项 （LCT4-LCT7） 可用作时钟信号，并可单独配置为乘积项或从逻辑块内部可用的 36 个信号创建的求和项方程。
4. 每个宏单元有一个专用的乘积项时钟。

输入时寄存器配置方式

XPLA3 器件宏单元的寄存器可以配置为输入寄存器;这意味着来自引脚的信号可以直接由寄存器锁存，而不必通过互连阵列。如下图所示，在实现输入寄存器时，前面的宏单元逻辑仍可用作埋入的组合节点。此逻辑可以反馈到互连阵列，以便在器件的其他位置进行分配。

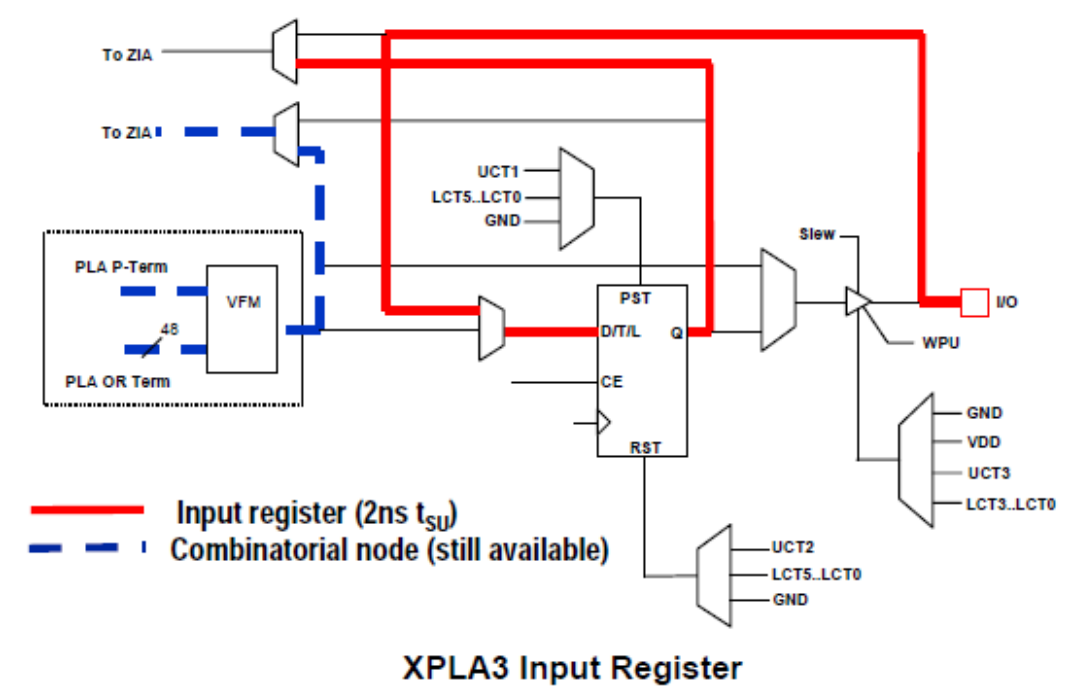
补充：埋在逻辑块中且未连接到I/O的宏单元与非埋入的宏单元的区别

埋在逻辑块中且未连接到 I/O 的宏单元与非埋入的宏单元相同，是因为它们都有相同的逻辑功能和结构。它们都可以支持组合或寄存器输入，通用预置和复位，可配置的 D, T, 或 L 寄存器，以及最大的时钟灵活性。它们都可以从 ZIA 获取 36 对真/反输入信号，以及 48 个产品项（PT）。它们都可以使用可变功能复用器（VFM）来实现任意两输入逻辑函数。它们都可以从 8个时钟源中选择一个，以及 8 个输出使能源中选择一个。它们都可以将逻辑输出反馈到 ZIA，供其他逻辑块使用。

因此，埋在逻辑块中且未连接到 I/O 的宏单元与非埋入的宏单元的唯一区别是，前者可以作为输入寄存器，直接从 I/O 引脚获取输入信号，而后者必须经过 ZIA 互连矩阵。这样可以提高输入信号的同步性和速度。但是，这并不影响它们的逻辑功能和结构，所以它们仍然是相同的。

I/O单元


7.5 FPGA-Field Programmable Gate Arrays

7.5.1FPGA制作工艺

反熔丝Anti-fuse (non-volatile)

反熔丝技术的优点是具有高抗干扰性、低功耗、高可靠性和高保密性，适合于要求稳定性和安全性的定型产品。反熔丝技术的缺点是只能一次性编程，不具备可重配置性。另外还可能发生电迁移。

SRAM

用交叉耦合的反相器锁存数据。

EPROM 和 E²PROM

EPROM (可擦可编程只读存储器) 是一种非易失性存储器，用于储存计算机固件或数据。它通过光学方式进行编程和擦除，需要特殊的设备和条件。它的特点是速度快，但不具有可重配置性。

EEPROM (电可擦可编程只读存储器) 也是一种非易失性存储器，与EPROM相比，它可以通过电信号进行编程和擦除，更加方便灵活。它的特点是具有可重写性，但速度较慢，寿命较短。

Flash

7.5.2 FPGA的结构

(1) Configurable logic block (CLB)
包含组合逻辑，寄存器
(2) Input/output block (IOB)
包含输入输出，三态控制
(3) Interconnect
具有可编程的开关，连接点
(4) B-SCAN
边界扫描单元，用于测试。

7.5.3 布尔方程和逻辑生成器

7.5.3.1 布尔方程

1. 最小项Min-Term

$F=f(A,B)$的最小项有四个----AB A’B B’A A’B’
对于N变量的函数，最小项有$2^N$个最小项

2. 正则表达式Canonical expressions

$f(x_1,x_2,\cdot \cdot \cdot ,x_n)={\sum }_{i=0}^{2^N-1}{\alpha }_i{m}_i,$
其中${\alpha }_i=0\mathrm{or}1$
所以正则表达式具有$2^{2^N}$种可能性

3.香浓扩展定理Shannon’s expansion theorem

$f(x_1,x_2,\cdots ,x_n)=x_{i}f(x_1,x_2,\cdots ,x_n){|}_{x_i=1}+\overline{x_i}f(x_1,x_2,\cdots ,x_n){|}_{xi=0}$

比如两个变量的扩展。
$f(x,y)=xf(1,y)+x\bar{f}(0,y)$

4. 正则定理Canonical theorem

N变量的布尔函数可以独一无二的表示成下面这种形式。
$\begin{array}{rl}f(x_1,x_2,\cdots ,x_n)& =f(1,1,\cdots ,1)x_1{x}_2\cdots x_n+f(1,1,\cdots ,0)x_1{x}_2\cdots x_n+\cdots +\\ & +f(0,0,\cdot \cdot \cdot ,0){\overline{x}}_1{\overline{x}}_2\cdot \cdot \overline{x_n}.\end{array}$

对于两个变量来说，形式如下
$f(x,y)=f(1,1)xy+f(1,0)xy+f(0,1)xy+f(0,0)x\overline{y}$

7.5.3.2 逻辑生成器

1. 基于PT原理

$f(x_1,x_2,\cdot \cdot \cdot ,x_n)={\sum }_{i=0}^{2^N-1}{\alpha }_i{m}_i$

2. 基于MUX原理

$f(x_1,x_2,\cdots ,x_n)=x_{i}f(x_1,x_2,\cdots ,x_n){|}_{x_i=1}+\overline{x_i}f(x_1,x_2,\cdots ,x_n){|}_{x_i=0}$

具体示例1

具体示例2

普适构造思路：不断地抽取系数，直至最后变成二变量布尔表达式。最后用很多个MUX把这些表达式串起来。

我们来分析具体怎么做的：

1. 把F中的B和/B提取出来将F改写成，$B\cdot (A+D)+\overline{B}\cdot (C+D)=B{F}_2+\overline{B}\cdot F_1$
2. 把F2中的A和/A提取出来将F2改写成$F_2=A+D=A\cdot 1+\overline{A}\cdot D$
3. 把F1中的C和/C提取出来将F1改写成$F_1=C+D=C\cdot 1+\overline{C}\cdot D$
4. F1和F2改写完已经是二值表达式了，所以最后可以用各种选择器实现了，注意提取出的系数作为控制端口。

3. 基于LUT原理

$\begin{array}{rl}f(x_1,x_2,\cdots ,x_n)& =f(1,1,\cdots ,1)x_1{x}_2\cdots x_n+f(1,1,\cdots ,0)x_1{x}_2\cdots x_n+\cdots +\\ & +f(0,0,\cdots ,0)\overline{x_1{x}_2}\cdots \overline{x_n}\end{array}$

原理：将布尔表达式的正则形式每种情况都算出来，把计算结果提前用D0和地址线存在锁存器里，后面碰到每种逻辑直接从锁存器里面读出来就好了。

7.5.4Configurable Logic Blocks

7.5.4.1. ACT Logic Modules

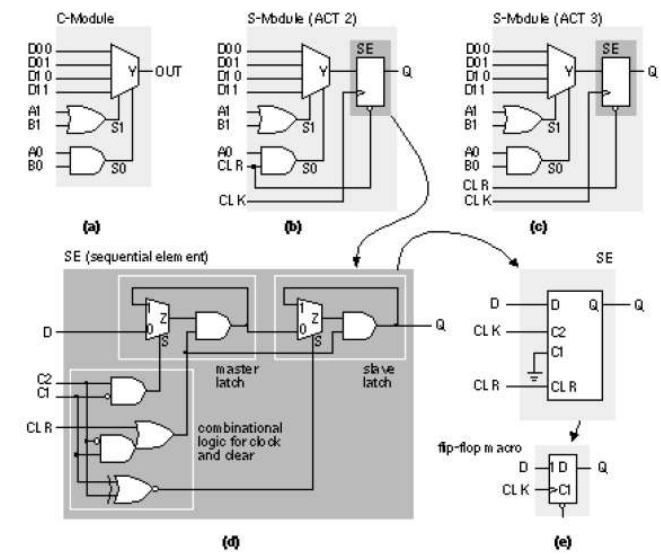
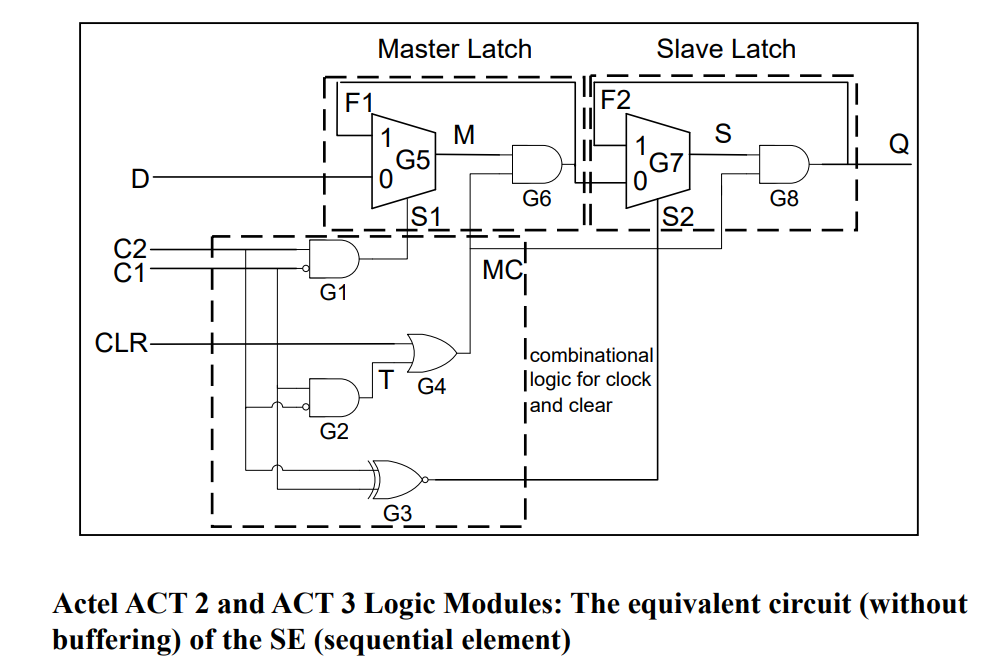
顺序单元 SE图如上。

7.5.4.2 XC 3000 CLB

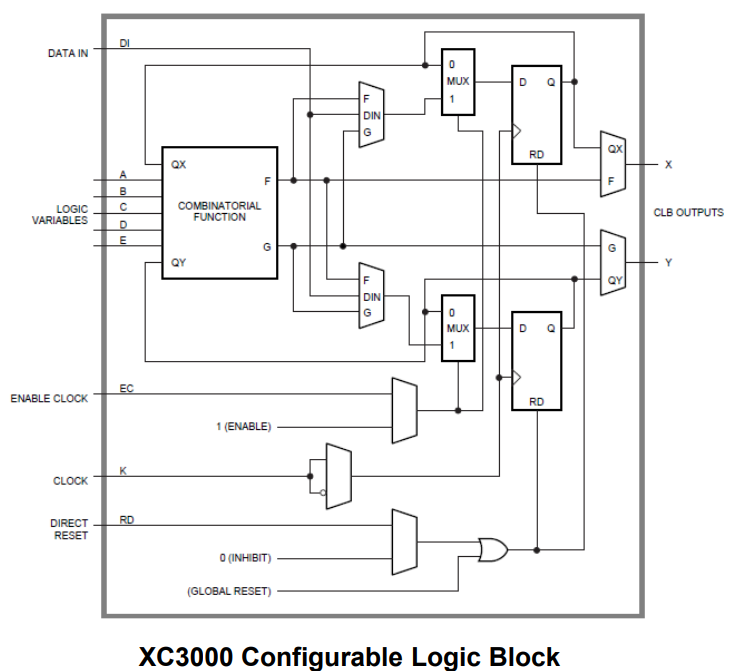
Combinational Logic Options:

下图是CLB中生成逻辑的部分。

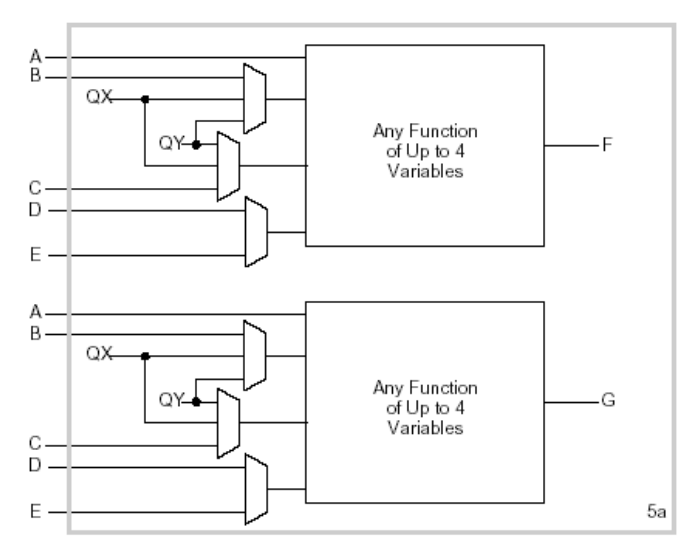
（a）组合逻辑选项FG生成两个函数，每个函数有四个变量。一个变量 A 必须对两个函数通用。第二个和第三个变量可以是 B、C、QX 和 QY 的任意选择。第四个变量可以是 D 或 E 的任意选择。

（b） 对于这部分图，组合逻辑选项 F 生成五个变量的任意函数：A、D、E 和 B、C、QX、QY 中的两个选项

（c） 组合逻辑选项 FGM 允许变量 E 在四个变量的两个函数之间进行选择：两者都具有共同的输入 A 和 D，其余两个变量具有 B、C、QX 和 QY 中的任意选择。然后，选项 3 可以实现 6 个或 7 个变量的一些函数。

我可以基于XC 3000 CLB的函数生成器来构造$F(A,B,C,D)=(A\cdot B)+(\overline{B}\cdot C)+D$，算是利用LUT构造布尔表达式方法的一种
$\begin{array}{rlrlr}& F(1,1,1,1)=1,& F(1,0,1,1)=1,& F(0,1,1,1)=1,& F(0,0,1,1)=1,\\ & F(1,1,1,0)=1,& F(1,0,1,0)=1,& F(0,1,1,0)=0,& F(0,0,1,0)=1,\\ & F(1,1,0,1)=1,& F(1,0,0,1)=1,& F(0,1,0,1)=1,& F(0,0,0,1)=1,\\ & F(1,1,0,0)=1,& F(1,0,0,0)=0,& F(0,1,0,0)=0,& F(0,0,0,0)=0.\end{array}$

我只要把输入选定成A、B、C、D四个，然后再配置LUT即可。

7.5.4.3 XC4000 CLB

相对XC3000 它更简单，而且有直通连线，如图红色部分。

1. 把XC4000 的逻辑生成器当RAM用

1. 16x2 (or 16x1) Edge-Triggered Single-Port RAM

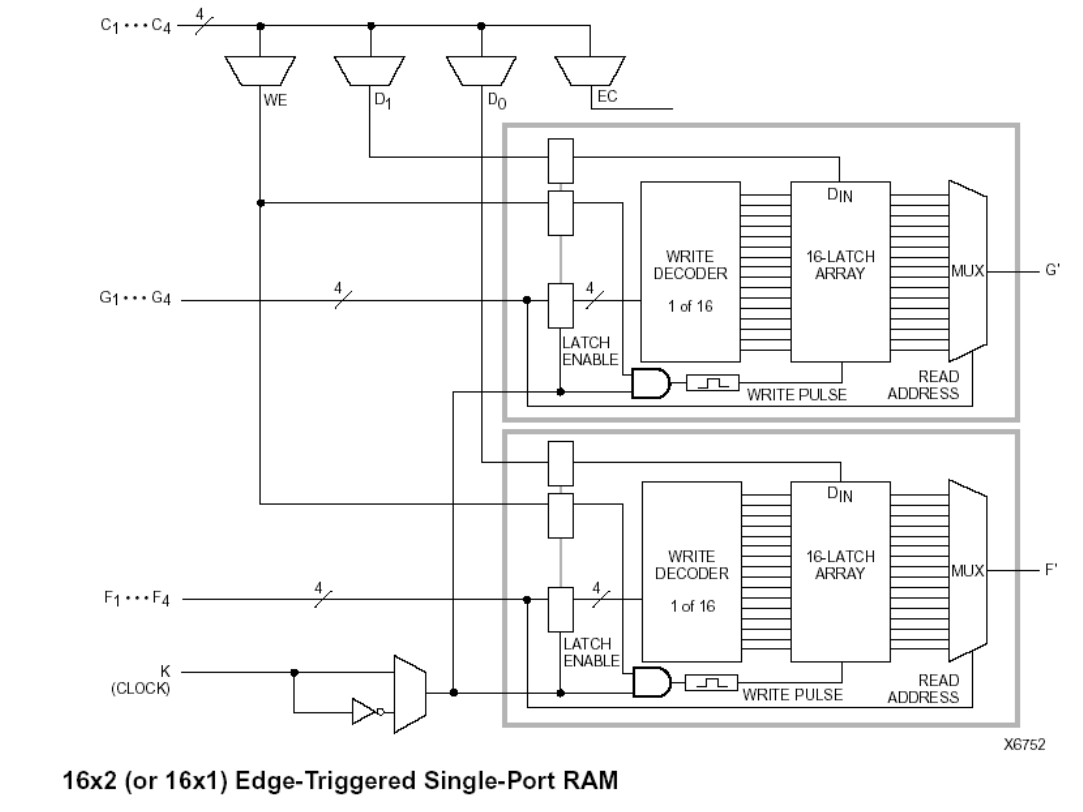
这两个RAM共享的就只有WE，CLOCK信号，地址线和数据输入都是各自有一个。

2. 32x1 Edge-Triggered Single-Port RAM (F and G addresses are identical）

把两块小RAM合成一块，地址从0~31，由A0~A4控制(注意A4在D1的位置)，D0是数据输入端口，WE控制写使能。

3. Dual-Port RAM, Simple Model

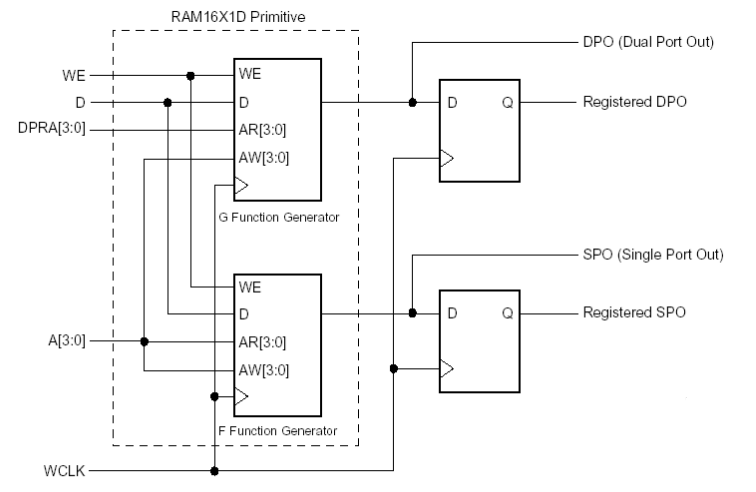
具体细节图如下

D0写进RAM1 和RAM2的数据是一样的，F1~F4控制写地址，G1~G4控制读地址

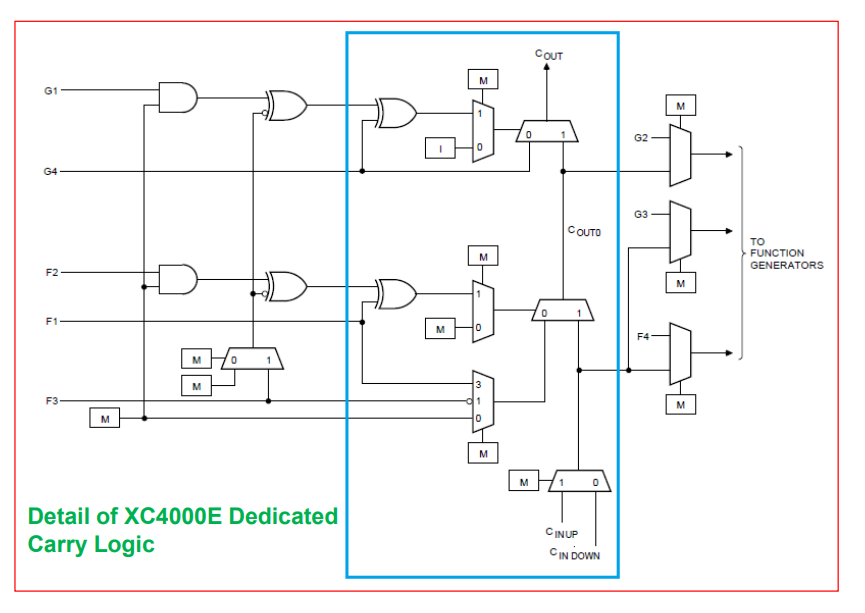
2. XC4000 中的超前进位链

7.5.5 可编程I/O

作用：

• 驱动片外输入的逻辑
• 接收并调理外部输入
• 静电保护

7.5.5.1 三态门

7.5.5.2 XC3000 I/O

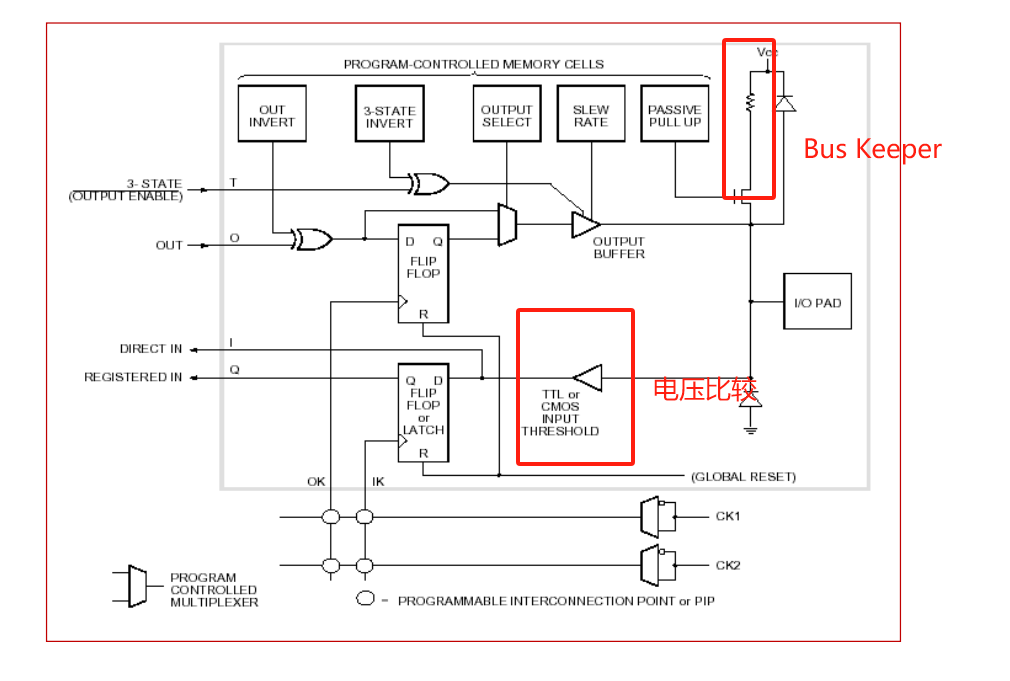
7.5.5.3 XC4000 I/O

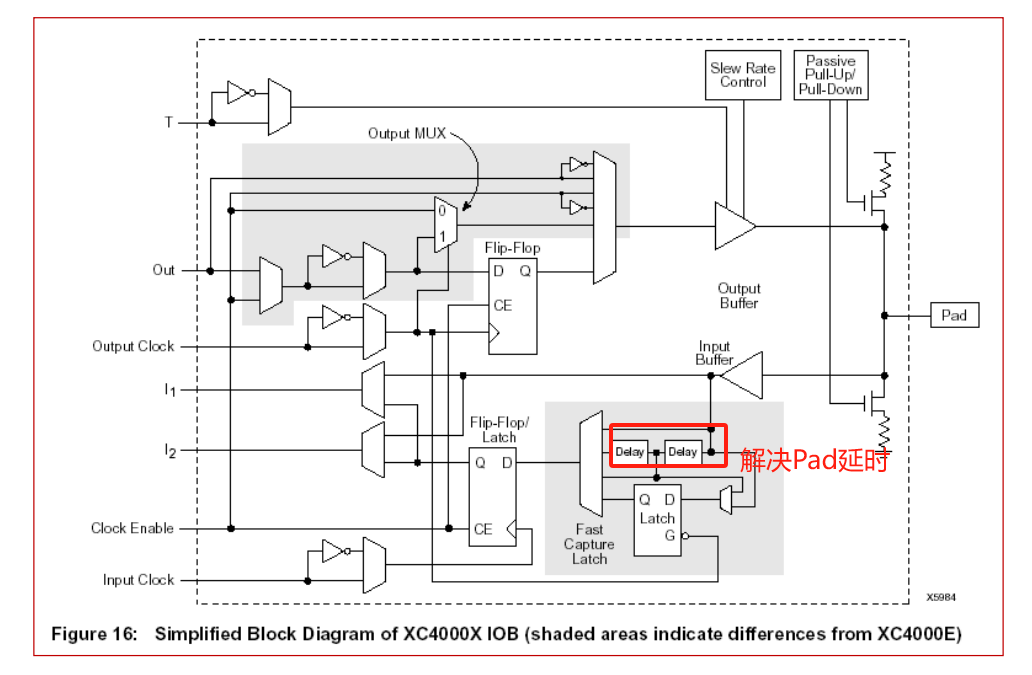
7.6 亚稳态Metastability

亚稳态是指触发器无法在某个规定时间段内达到一个可确认的状态。当一个触发器进入亚稳态引时，既无法预测该单元的输出电平，也无法预测何时输出才能稳定在某个正确的电平上。在这个稳定期间，触发器输出一些中间级电平，或者可能处于振荡状态，并且这种无用的输出电平可以沿信号通道上的各个触发器级联式传播下去。

触发器的建立时间和保持时间在时钟上升沿左右定义了一个时间窗口，如果触发器数据输入端口上的数据在这个时间窗口内发生变化（或者数据更新），那么就会产生时序违规。存在这个时序违规是因为违反了建立时间要求和保持时间要求，此时触发器内部的一个节点（一个内部节点或者要输出到外部节点）可能会在一个电压范围内浮动，无法稳定在逻辑0或者逻辑1状态。换句话说，如果数据在上述窗口中被采集，触发器中的晶体管不能可靠地设置为逻辑0或者逻辑1对应的电平上。所以此时的晶体管并未处于饱和区对应的高或者低电平，而是在稳定到一个确定电平之前，徘徊在一个中间电平状态（这个中间电平或许是一个正确值，又或许不是）。

个人认为：在同步系统中输入信号我们会设计成让其满足触发器的时序要求，所以不会发生亚稳态。但是，在异步系统中，由于数据和时钟的关系不是固定的，因此有时会出现违反建立和保持时间的现象。

当触发器处在亚稳态时，输出会在高低电平之间波动，这会导致延迟输出转换过程，并超出所规定的时钟到输出的延迟值( tco)。亚稳态输出恢复到稳定状态所需的超出tco的额外时间部分称为稳定时间 ( tMET)。一般来说，触发器都会在一个或者两个时钟周期内从亚稳态返回稳态。所以我们加两级触发器，这个亚稳态信号就可能变成稳态信号

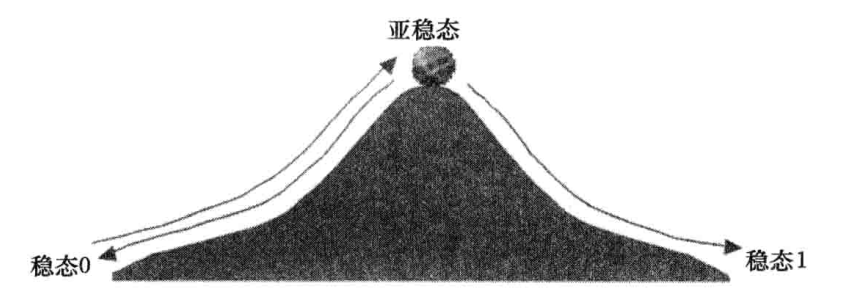
更形象的看待亚稳态，如下图所示，触发器的运转类似于在光滑的山上滚动球，山的两边代表两个稳定状态（即高和低)，山顶就代表亚稳态。假设球处在一个稳定的状态（即1或0)，给球一个足够（满足建立和保持时间要求)的推力（状态转换)，使这个球在规定时间内越过山顶到达另一个稳定的状态。然而，如果推力不够（即违反建立和保持时间)，这个球就会到达山顶（即输出亚稳态)，停留一段时间后再返回到一个稳定的状态（即最终输出稳定)。这个球也可能会上升一段路程就返回了（即输出可能产生毛刺)。这两种情况都会增加从时钟变化到稳定输出的延迟。

具体从亚稳态输出到稳态输出延迟的时序图如下所示。
图中tr表示延迟的时间。