本文主要是介绍高中数学:分段函数的零点问题(拔高),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、核心思想
1、分段函数分段看
2、零点与交点的互换
3、画函数图像,观察零点或交点个数
4、联立方程,看根的个数,即为交点个数
二、例题
例题1
解题思路:
1、画分段函数图像
2、绝对值的解析式,分类讨论,分区间画图
3、f(x)=af(x+T),a≠0&T≠0是周期函数,且每个周期上的函数值是上一个周期的a倍
4、用联立方程的方法,验证图像交点个数

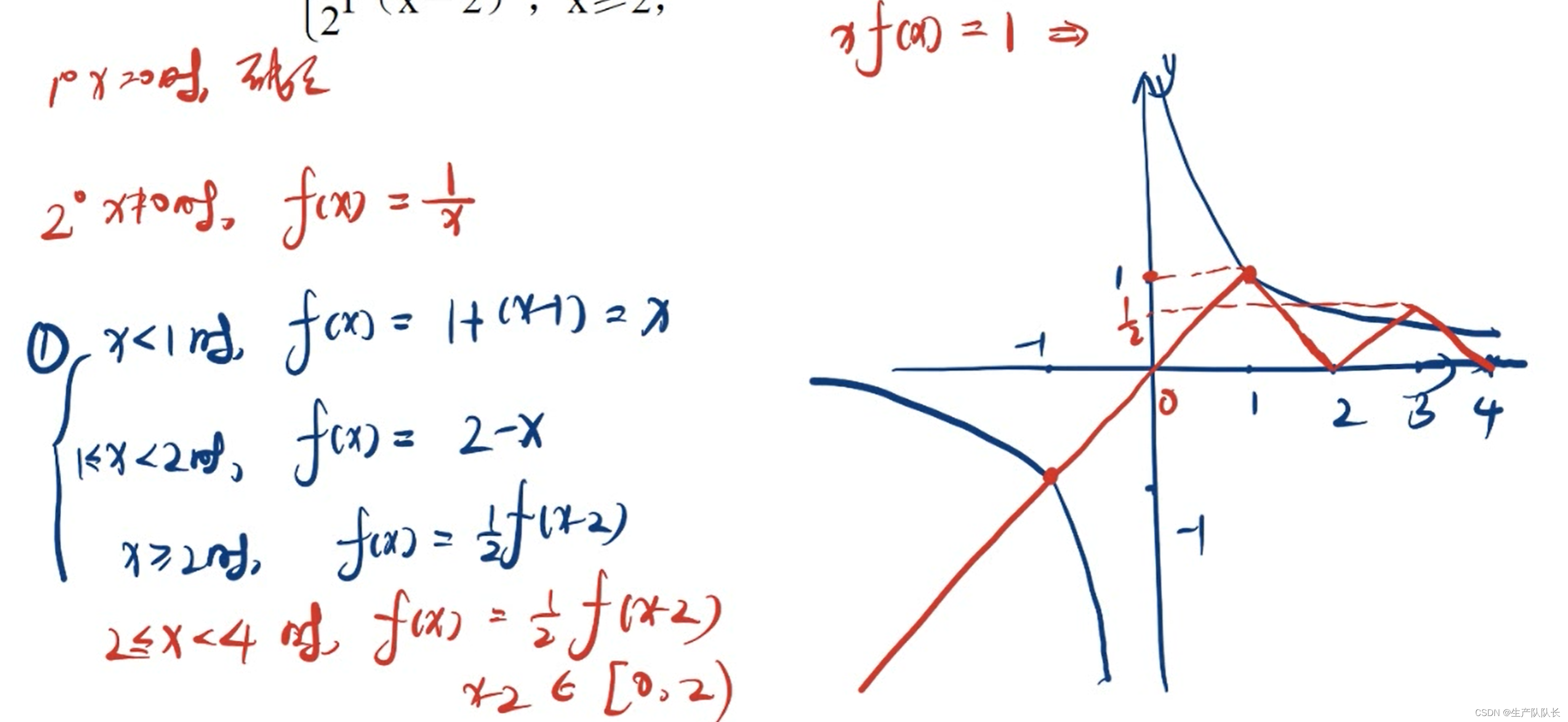
例题2(重点)
难点:
含参数分段函数,求参数范围
迭代复合函数
解题思路:
1、画草图
2、零点问题转化成交点问题
3、迭代复合函数,换元,构建方程组

解题步骤:
1、草图
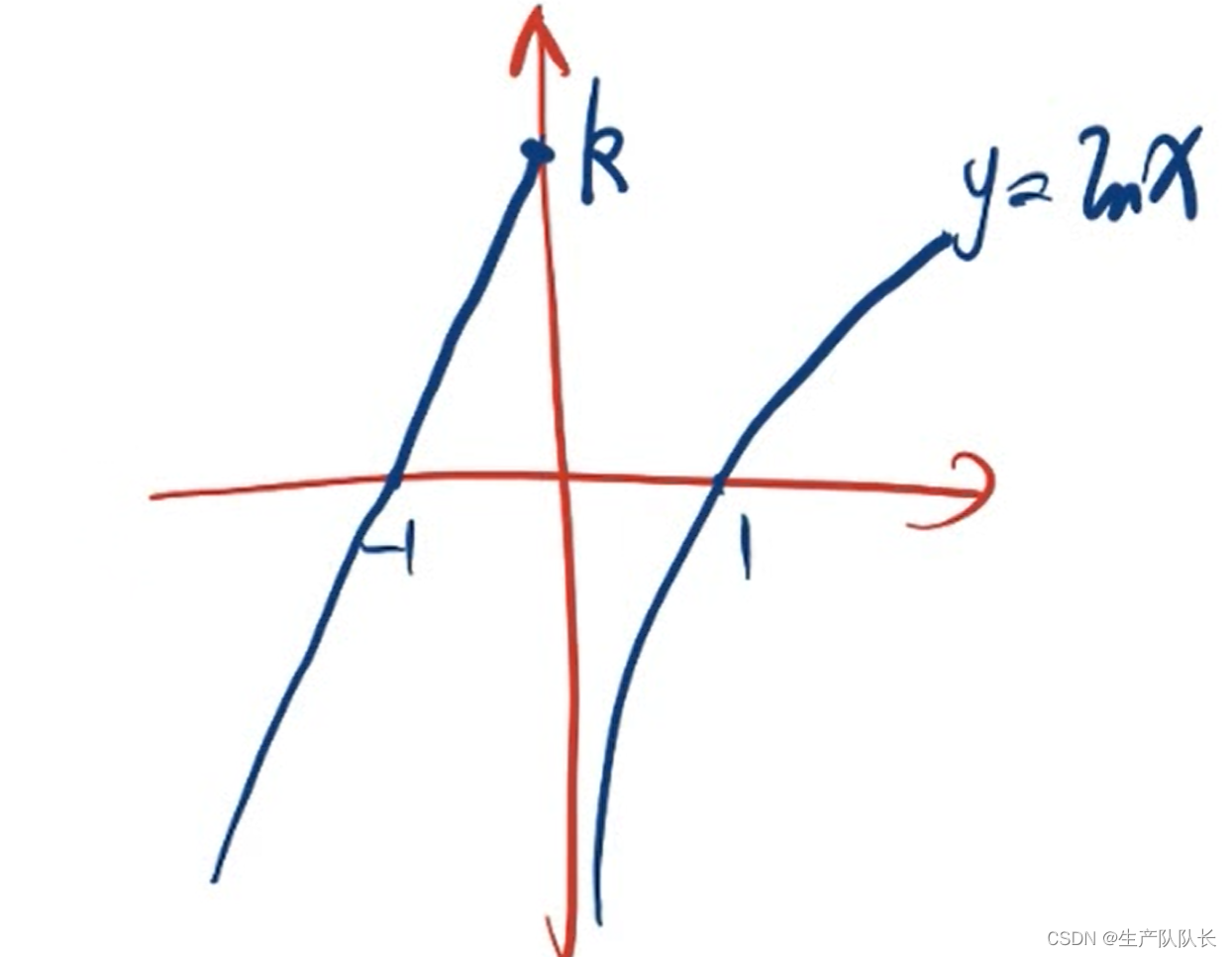
2、零点问题转化成交点问题
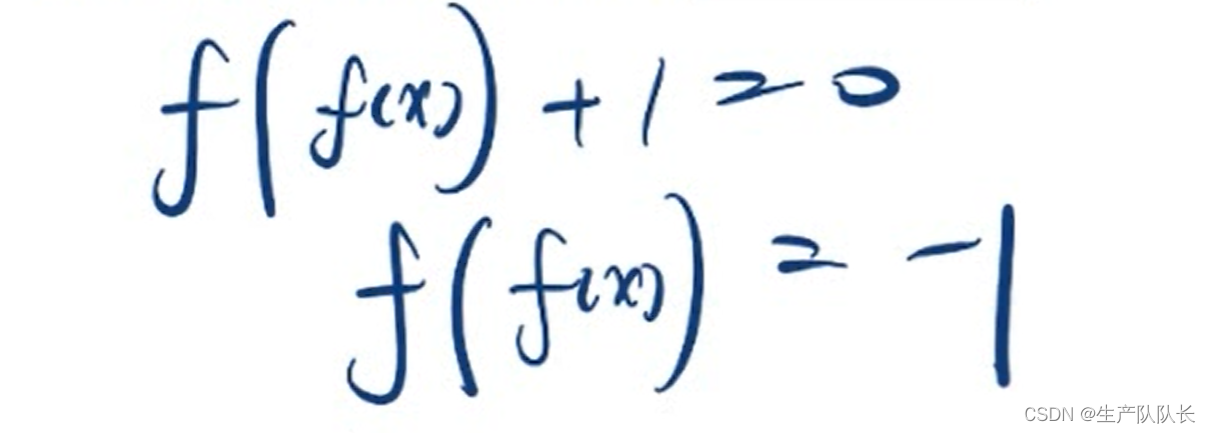
3、换元构建方程组
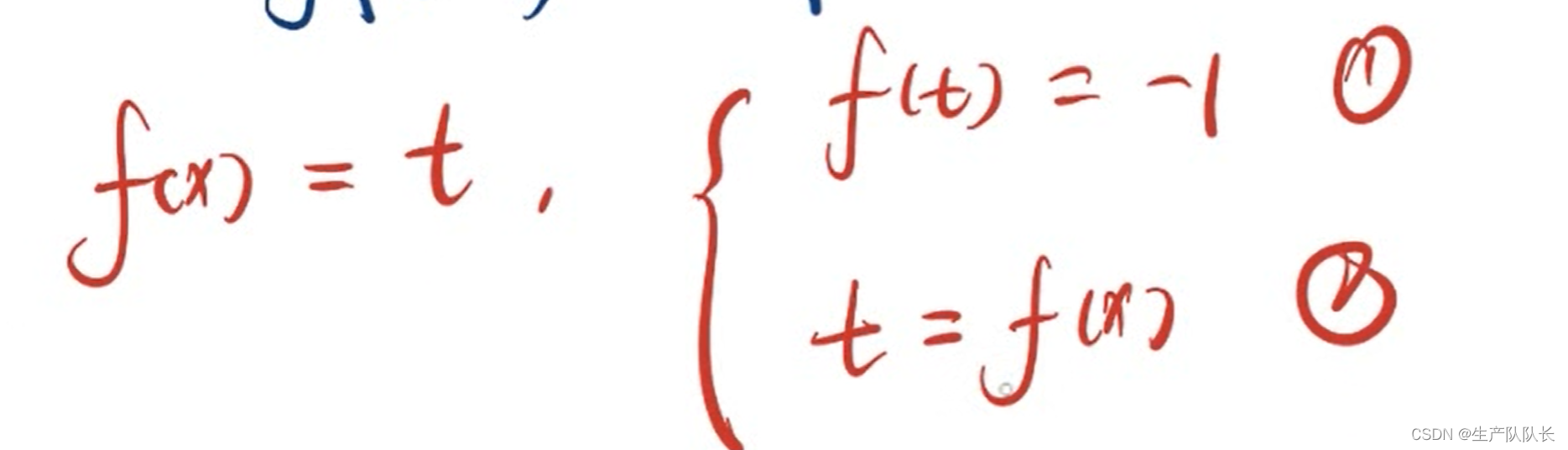
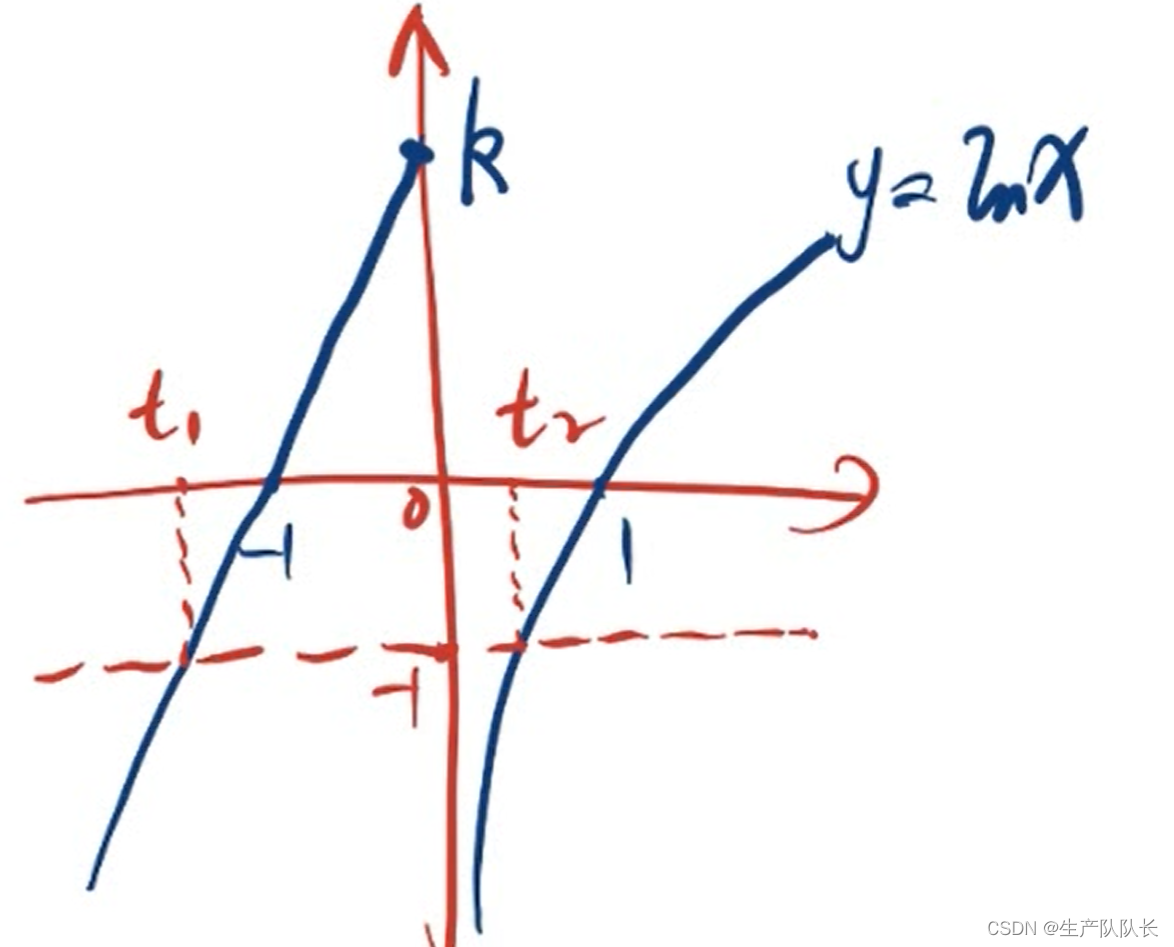
4、根据条件,解方程组,得出最终结论
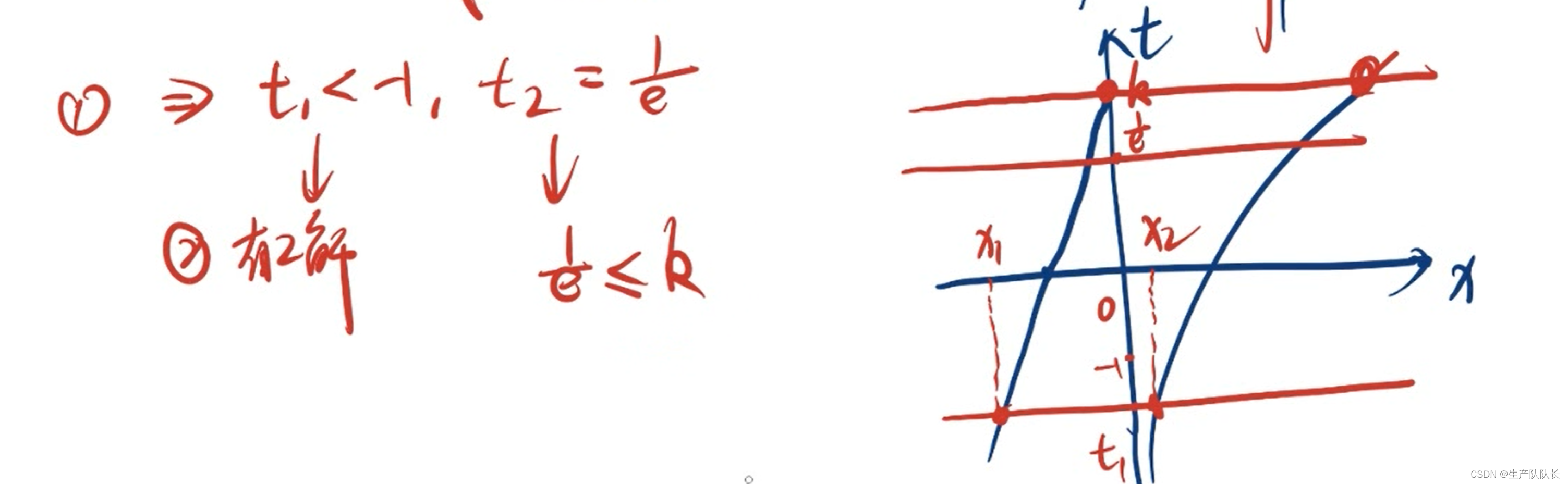
例题3(重点)
难点:
含参数,求参数范围
分段函数相加:需要进行区间划分,相同区间上的函数才可以相加
解题思路:
1、待求函数进行变形,转化成交点问题
2、两组分段函数按区间相加
3、画草图,根据图像找复合要求的交点

解题步骤:
1、转化成交点问题

2、分段函数相加
这里区间的划分:因为f(x)是R上的分段函数,f(2-x)也是R上的函数,但是,划分点,是0和2
所以,一定是把R划分成了三个区间(-∞,0)、(0,2)、(2,+∞)
然后,对应区间上的表达式相加即可
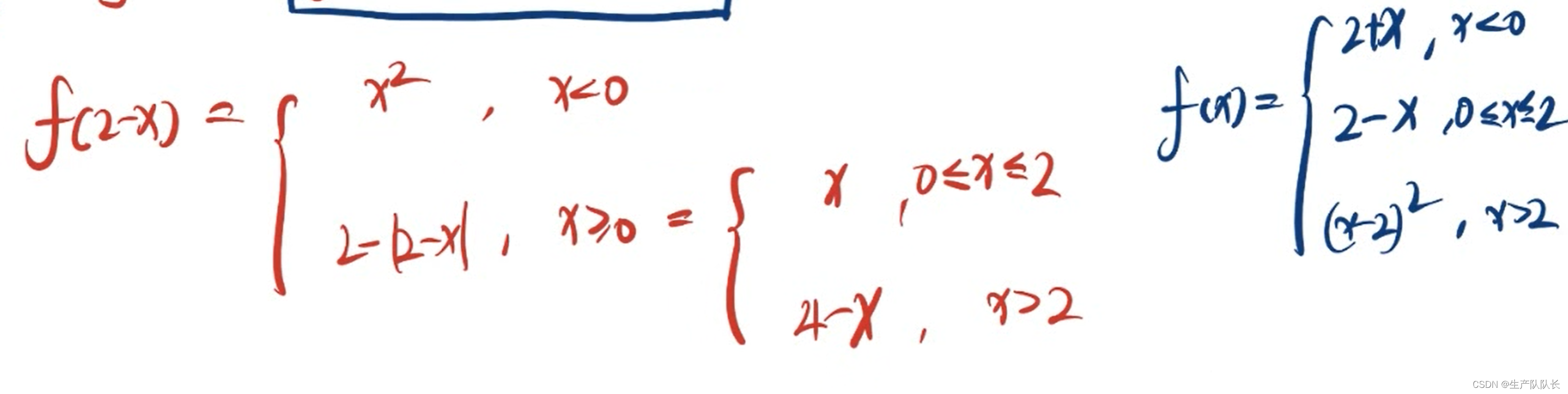
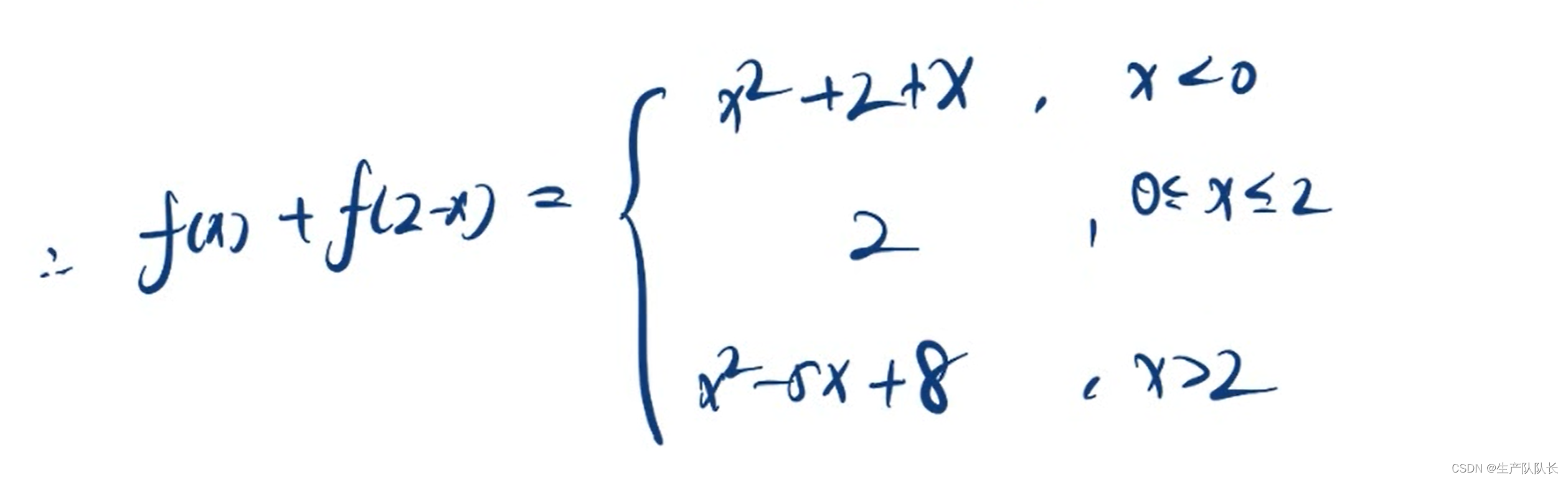
3、画草图,求解
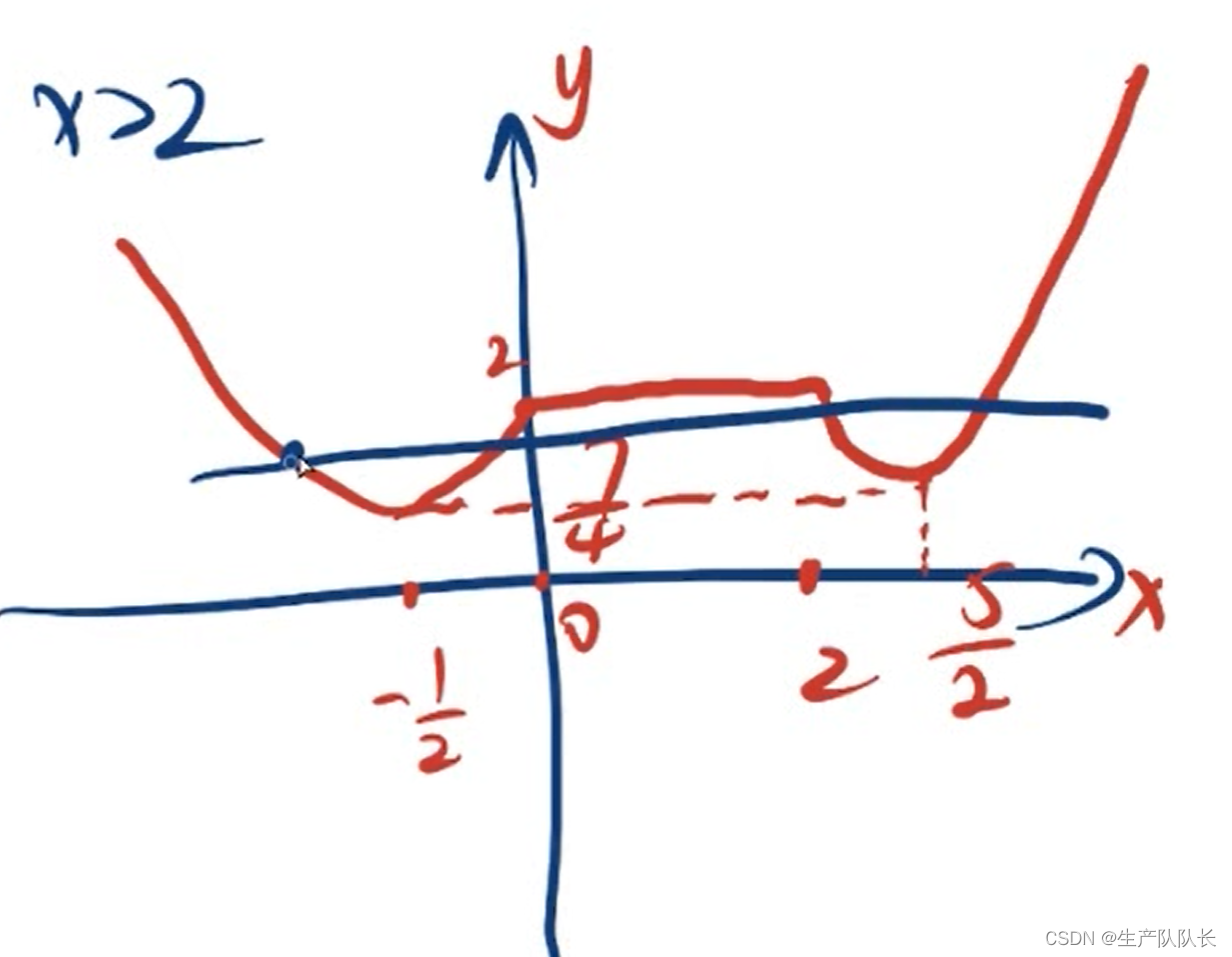
这篇关于高中数学:分段函数的零点问题(拔高)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





