codeforces round.906 - E - Mirror Grid （数学，坐标变换）

本文主要是介绍codeforces round.906 - E - Mirror Grid （数学，坐标变换），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

You are given a square grid with n rows and n columns. Each cell contains either $0$ or $1$.

In an operation, you can select a cell of the grid and flip it (from $0\to 1$ or $1\to 0$). Find the minimum number of operations you need to obtain a square that remains the same when rotated $0\circ ,90\circ ,180\circ$ and $270\circ$.

The picture below shows an example of all rotations of a grid.

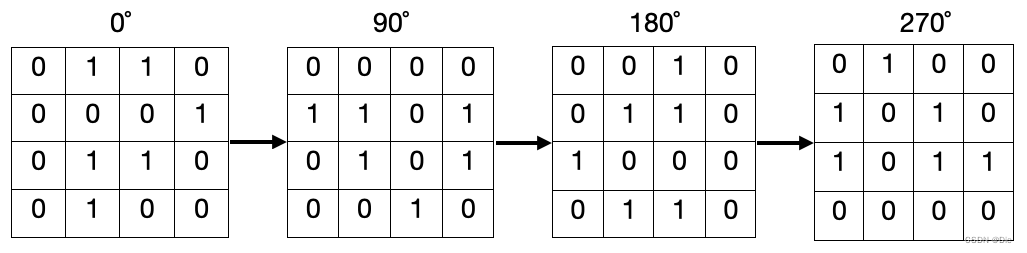
Input

The first line contains a single integer $t$ $(1\le t\le 100)$ — the number of test cases.

The first line of each test case contains a single integer $n$ $(1\le n\le 100)$ — the size of the grid.

Then $n$ lines follow, each with $n$ characters $a_{i,j}$ $(0\le a_{i,j}\le 1)$ — the number written in each cell.

Output

For each test case output a single integer — the minimum number of operations needed to make the square look the same rotated $0\circ ,90\circ ,180\circ and270\circ$.

Sample 1

Input

5
3
010
110
010
1
0
5
11100
11011
01011
10011
11000
5
01000
10101
01010
00010
01001
5
11001
00000
11111
10110
01111

Output

1
0
9
7
6

首先：这题不是找规律的题，如果要满足怎么转都是一样的，这个图形就要满足中心对称，如果要满足中心对称就要满足向以下图形一样：

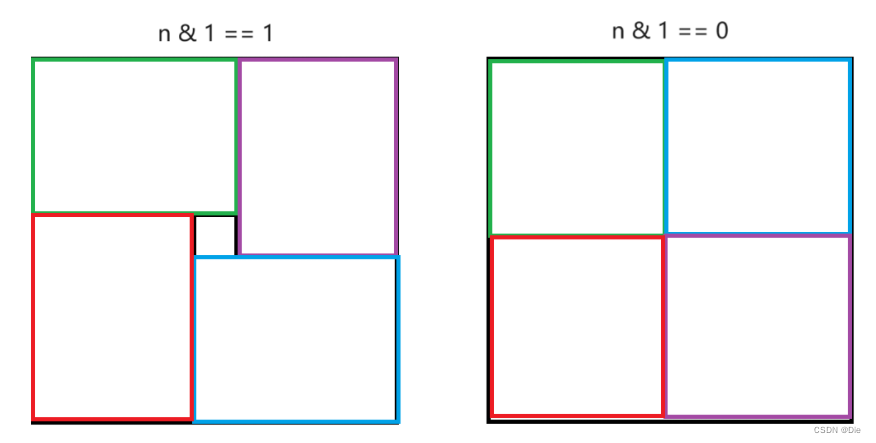
首先绿色方块中的每个点转到其他任何方块对应的点都应该是相同的，只有满足了这个规律才能够成为中心对称图形，而中心对称图形在行列数为奇数和偶数的时候是不同的。

如果在绿色区域内的点的坐标为(x,y)，那么转到其他三个区域对应的点分别是：$(y,n-x-1),(n-x+1,n-y+1),(n-y+1,x)$。

由于只有0和1，所以只要求出来这四个点的加和，如果为 $1$ 或者 $3$，那么就是有 $1$ 个 $1$ 或者 $1$ 个 $0$，那么这种情况只需要改变一个值，那么就让答案加 $1$，如果是 $0,4$，那就不用改变，如果为 $2$，那就要改变两次。

代码：

#include<iostream>
using namespace std;
const int N = 110;int g[N][N];
int n;int main() {int t; cin >> t;while (t--) {cin >> n;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {char c; cin >> c;g[i][j] = c - '0';}}int res = 0;if (n & 1) {for (int i = 1; i <= n / 2; i++) {for (int j = 1; j <= n / 2 + 1; j++) {int x1 = j, y1 = n - i + 1;int x2 = n - i + 1, y2 = n - j + 1;int x3 = n - j + 1, y3 = i;int sum = g[i][j] + g[x1][y1] + g[x2][y2] + g[x3][y3];if (sum == 1 || sum == 3)res += 1;if (sum == 2)res += 2;}}}else {for (int i = 1; i <= n / 2; i++) {for (int j = 1; j <= n / 2; j++) {int x1 = j, y1 = n - i + 1;int x2 = n - i + 1, y2 = n - j + 1;int x3 = n - j + 1, y3 = i;int sum = g[i][j] + g[x1][y1] + g[x2][y2] + g[x3][y3];if (sum == 1 || sum == 3)res += 1;if (sum == 2)res += 2;}}}cout << res << endl;}return 0;
}

这篇关于codeforces round.906 - E - Mirror Grid （数学，坐标变换）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---