本文主要是介绍CS131学习笔记(lecture4),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
课程讲义:http://vision.stanford.edu/teaching/cs131_fall1718/files/04_filters.pdf
图像采样(sampling)和量化(quantization)
首先,自然界中的每一景象都是“continuous”,然而这在计算机的世界观中是不可接受的。所以必须把模拟信号进行采样和量化才能得到图像矩阵,当然了,这一过程产生误差和丢失信息也是不可避免的。图像矩阵的每一个元素都是一个像素点(pixel dot,以下像素点和矩阵元素等价),分辨率(resolution, 单位dpi,dots per inch)表示单位面积之内的像素点个数,当图像矩阵确定时,仅和人眼的直接观察效果有关。像素点的内容决定了图片的类型:
黑白图片:矩阵元素是0-1binary,0表示黑,1表示白。
灰阶图片:矩阵元素是[0,N],0表示黑,N表示白,共切割为N-1阶。
彩色图片:矩阵元素是[0,N],按照一定的标准(如RGB, Lab, HSV, etc.)可以覆盖常见色域的N-1种颜色
##图像直方图(histogram)
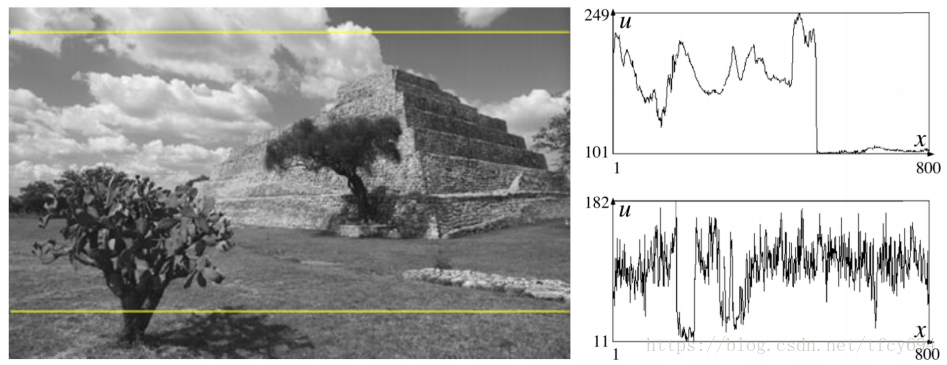
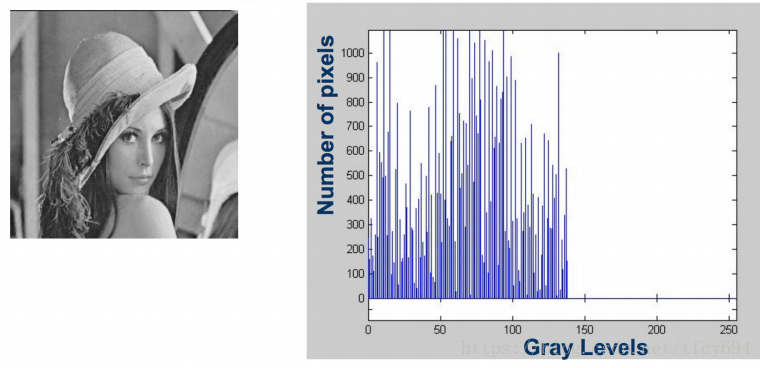
概念同统计学中的直方图概念,即:对一定范围内(如每行、每图像块、每幅全图像,etc.)的像素点,按照各个像素的值进行频数统计并作图。
图像函数
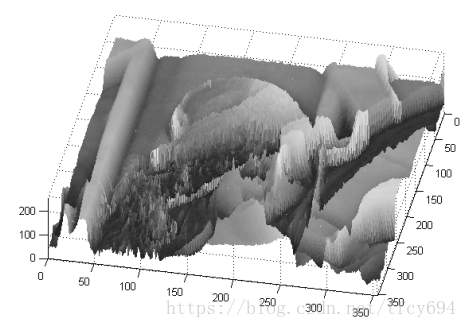
前面我们是通过矩阵的角度理解“图像”的,换个角度,把一幅“图像”看作一个函数,定义域是全体像素坐标,映射关系是每个像素坐标处对应的像素值。有了“函数”的抽象,则可以利用信号与系统的知识对函数进行operate。
线性系统(滤波器(filter))
滤波器是处理一幅图获得另一幅图的装置(或者函数、系统等等任何方便理解的名词都可),文中举了移动平均和阈值两种滤波器。其系统函数分别如下:
g ( n , m ) = 1 9 ∑ k = n − 1 n + 1 ∑ l = m − 1 m + 1 f [ k , l ] g(n, m)=\dfrac{1}{9}\sum\limits_{k=n-1}^{n+1} \sum\limits_{l=m-1}^{m+1} f[k,l] g(n,m)=91k=n−1∑n+1l=m−1∑m+1f[k,l]
g ( n , m ) = { 1 , f ( n , m ) ≥ a 0 , f ( n , m ) < a g(n, m)=\left\{\begin{array}{cc} 1, & f(n, m)\geq a\\ 0, & f(n, m)< a \end{array}\right. g(n,m)={1,0,f(n,m)≥af(n,m)<a
以下知识主要基于《信号与系统》和《离散时间信号处理》:
1.线性(linear)系统S[f(x, y)]的定义主要有来自两条:
数乘条件: S [ α f ( n , m ) ] = α S [ f ( n , m ) ] S[\alpha f(n, m)]=\alpha S[ f(n, m)] S[αf(n,m)]=αS[f(n,m)]
可加条件: S [ f i ( n , m ) + f j ( n , m ) ] = S [ f i ( n , m ) ] + S [ f j ( n , m ) ] S[f_i(n, m)+f_j(n, m)]=S[f_i(n, m)]+S[f_j(n, m)] S[fi(n,m)+fj(n,m)]=S[fi(n,m)]+S[fj(n,m)]
综合等价于为: S [ α f i ( n , m ) + β f j ( n , m ) ] = α S [ f i ( n , m ) ] + β S [ f j ( n , m ) ] S[\alpha f_i(n,m)+\beta f_j(n,m)]=\alpha S[f_i(n,m)]+\beta S[f_j(n,m)] S[αfi(n,m)+βfj(n,m)]=αS[fi(n,m)]+βS[fj(n,m)]
2.移不变(shift invariant)系统的要求:若 g ( n . m ) = S [ f ( n , m ) ] g(n.m)=S[f(n,m)] g(n.m)=S[f(n,m)],则 g ( n − s , m − t ) = S [ f ( n − s , m − t ) ] g(n-s,m-t)=S[f(n-s,m-t)] g(n−s,m−t)=S[f(n−s,m−t)]
如无特殊说明,本文所指的“系统”均为线性移不变系统(LSI),除了前述3个条件外,其他条件重要性略低,可参考上述两书,此处不再赘述。
另有冲激函数 δ ( m , n ) \delta(m, n) δ(m,n)的定义:此函数在原点处的值为1,在其他处的值为0。
则所有图像函数都可以看作产生位移的冲激函数的线性组合,对于原函数的operate可以由移不变性质转化为对于冲激函数的operate,大大化简了信号处理过程。
卷积(convolution)
卷积的表达式: f ∗ g ( n , m ) = ∑ l ∑ k f ( k , l ) g ( n − k , m − l ) f*g(n, m)=\sum_{l} \sum_{k} f(k,l)g(n-k,m-l) f∗g(n,m)=∑l∑kf(k,l)g(n−k,m−l)
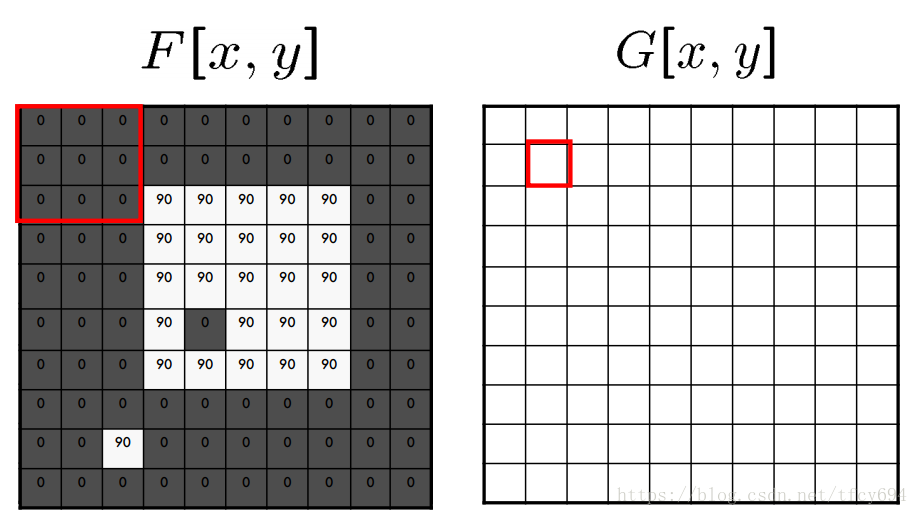
信号输入LSI系统进行process的过程可以看作和系统函数进行卷积的过程。值得注意的是,卷积表达式是无穷的,而图片和计算机处理过程通常是有限的,所以必须考虑边缘效应(edge effect)。如图,对F进行九宫格移动平均得到等大的G,其中计算G左上角格时F的边缘溢出,需要进行扩展(pad),即假设溢出区域的值用于计算,padding的方案包括用0pad、边缘值pad等。
相关(correlation)
顾名思义,相关是用来描述两幅图像内容相似度的函数。定义式如下:
r f ∗ ∗ g ( k , l ) = ∑ m ∑ n f ( n , m ) g ∗ ( n − k , m − l ) = ∑ m ∑ n f ( n + k , m + l ) g ∗ ( n , m ) = f ( k , l ) ∗ g ∗ ( − k , − l ) r_{f**g}(k,l)=\sum_{m} \sum_{n} f(n,m)g^{*}(n-k,m-l)=\sum_{m} \sum_{n} f(n+k,m+l)g^{*}(n,m)=f(k,l)*g^{*}(-k,-l) rf∗∗g(k,l)=m∑n∑f(n,m)g∗(n−k,m−l)=m∑n∑f(n+k,m+l)g∗(n,m)=f(k,l)∗g∗(−k,−l)
上式中 g ∗ g^{*} g∗表示g的共轭对称函数。在实值函数中为g本身。
这篇关于CS131学习笔记(lecture4)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!