python实现时序平滑算法SG滤波器

本文主要是介绍python实现时序平滑算法SG滤波器，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972

   个人介绍: 研一｜统计学｜干货分享
         擅长Python、Matlab、R等主流编程软件
         累计十余项国家级比赛奖项，参与研究经费10w、40w级横向

该篇文章针对火焰光谱数据使用S-G平滑滤波对原始光频信息本身带有的较多的噪声信号的火焰毛刺数据进行处理，减少由于噪声导致的对火焰有效红外光谱特征数据的正确获取结果产生较大的影响，包括模型原理，Python实操及对应的可视化分析和结果解读。

1 简介

  S-G （Savitzky-Goloy）滤波器率由Savizky 、 Golay两人共同提出，该方法在时间序列这一领域中得到了广泛的应用。最小二乘法拟合的原理，是S-G平滑滤波的基础原理，针对需要处理的数据，通过多项式加权拟合方式，同时结合一定长度窗口的大小，最终获取最小均方根误差。陈晋等人通过实验验证指出S-G滤波器参数m、d的推荐的取值范围分别为2至7、2至4，本次演示最终选取C-G滤波器参数m=6，d=3。S-G基本平滑原理如式：

$$Y_{(2m+1)\times 1}=X_{(2m+1)\times d}{A}_{d\times 1}+E_{(2m+1)\times d}$$

  其中：$Y$为某一窗口拟合值矩阵；$X$表示变量矩阵；$A$表示多项式拟合系数矩阵；$E$表示残差矩阵；m表示半窗口大小；d-1表示拟合最大次数；N 为窗口大小，其中N值大小符合 N = 2m + 1。

  原理图展示：

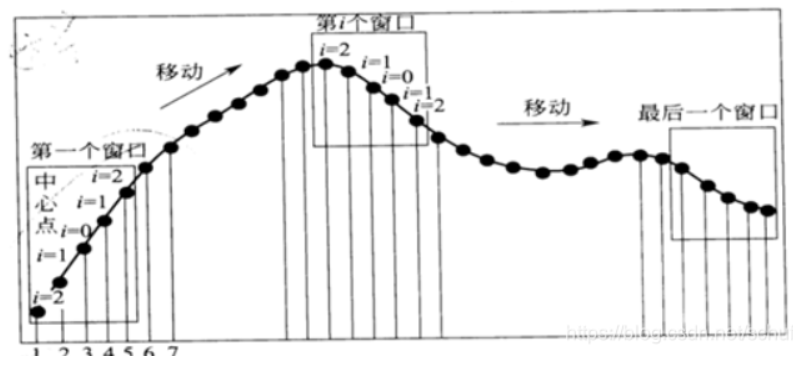
  把光谱一段区间的等波长间隔的5个点记为X集合，多项式平滑就是利用在波长点为Xm-2,Xm-1,Xm,Xm+1,Xm+2的数据的多项式拟合值来取代Xm,，然后依次移动，直到把光谱遍历完。

2 数据背景

  本次演示中所用数据均来源于2016年的APMCM竞赛的A题数据（下载地址 ），官网提供的数据文件中包含着3组金属冶炼过程中照片探测器监测得到的光谱信息数据。每组数据文件变量共涉及时间t（间距0.5s）、炉内燃烧气体的累积消耗Q、燃烧气体的累积消耗比p、光学信息的数据(f_1-f_2048、不同频率光强)、开尔文温度t和关键元素碳含量共2053个属性。

  火焰在人的肉眼观察情况下存在有不同的焰火颜色的变化，其根本原因是因为火焰燃烧过程中火焰的光谱情况的变化。因此利用光电探测器采集得到的火焰光谱实验数据呈现渐进式变化过程（见下图）。

  该图像刻画出了第一组实验数据炉内进行转炉炼钢的同时，每间隔0.5s炉内各波长光谱数据强度情况，可以看到在连续监测过程中，每一次监测得到的火焰光谱各波长强度情况存在具较高相似度，存在明显规律性。每一次监测中，波长由低到高总体均呈现“平缓-急剧上升-急剧下降-缓慢上升-缓慢下降”的变化特征，且高峰数据多集中于波长段“f_1200-f_1300”之间。

3 S-G平滑滤波实操

  考虑到若直接利用通过红外光电探测器所收集获取得到的火焰原始红外光谱信息进行炉转终点温度及碳元素含量预测，可能会由于原始光频信息本身带有的较多的噪声信号的火焰毛刺数据，进而会对火焰有效红外光谱特征数据的正确获取结果产生较大的影响，因此，该演示将利用Savitzky-Goloy滤波器技术对光电探测器所获得火焰的红外原始光谱数据进行光谱数据预处理，对其进行平滑操作减少噪声数据带来的影响。下图表示为原始红外光谱数据预处理完成后得到的火焰光谱各波长强度情况。

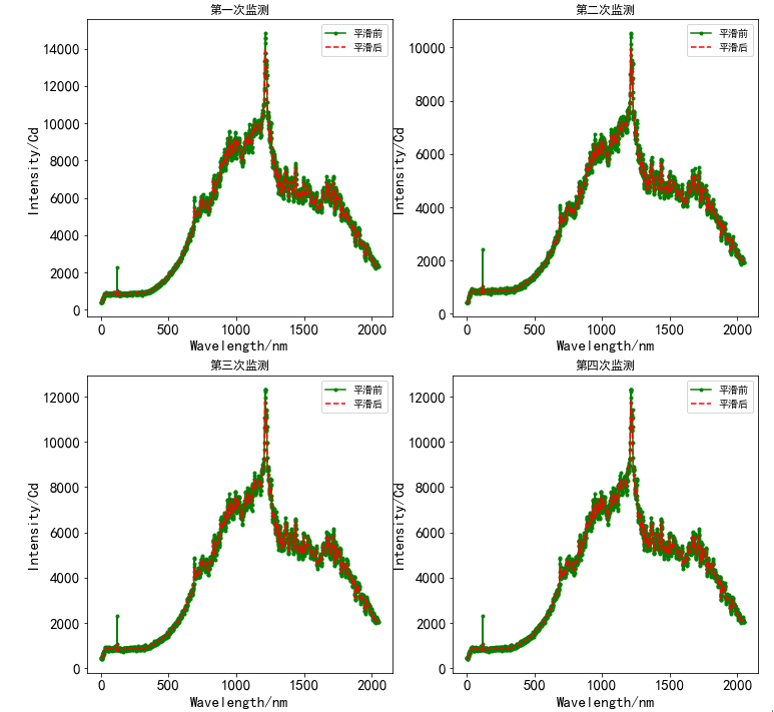
  通过上图可以看出，与平滑前光谱的数据相比，该图中的显著突出数据明显得到改善，且平滑后并未对光谱波长强度总体分布特征造成影响，为进一步查看观测Savitzky-Goloy平滑滤波器应用于光谱信息上的效果，本实验绘制了第一组前四次监测的火焰光谱数据平滑前后效果，见下图所示。

  通过上图可以看出，平滑前部分毛刺数据经过Savitzky-Goloy滤波后得到很好的处理，特别是对于异常凸起的毛刺数据，认为原始红外光谱数据通过Savitzky-Goloy滤波器技术对噪声数据有着明显的改进效果。

4 完整代码

from matplotlib import pyplot as plt
from scipy.signal import savgol_filter##Savitzky-Golay 平滑
import numpy as np  
import openpyxl 
import pandas as pd##初始绘三维图
df=pd.read_excel('D:\\1 - 副本.xlsx')#读取数据
height,width = df.shape
print(height,width,type(df))#数据大小
##提取光信息特征
data2=df.iloc[:,3:2051]#光学频率：1-2048
from matplotlib import pyplot as plt
%matplotlib inline
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
x = np.arange(0,2048)
y = np.arange(0,404)
X, Y = np.meshgrid(x, y)
Z = np.array(data2)# 具体函数方法可用 help(function) 查看，如：help(ax.plot_surface)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
ax.set_zlim(0, 25000)
ax.set_xlabel('Wavelength/nm')
ax.set_ylabel('Frame')
ax.set_zlabel('Intensity/Cd')
plt.show()
# 设置坐标轴的名称##Savitzky-Golay 平滑
df=pd.read_excel('C:\\3 - 副本.xlsx')#读取数据
height,width = df.shape
print(height,width,type(df))#数据大小
data=df.iloc[:,3:2051]#光学频率：1-2048newans=pd.DataFrame()
for i in range(286):data0=data.loc[i]newans1 = savgol_filter(list(data0), 17, 3, mode= 'nearest')newans2 =pd.DataFrame(newans1).Tnewans=newans.append(newans2)data1 = pd.DataFrame(newans.values, index=data.index, columns=data.columns)##更改行列名data1["t"]=df.iloc[:,0]
data1["Q"]=df.iloc[:,1]
data1["P"]=df.iloc[:,2]
data1["T(K)"]=df.iloc[:,2051]
data1["C"]=df.iloc[:,2052]
data1.to_excel('C:\\平滑后3.xlsx',index=False)##绘制三维图df=pd.read_excel('C:\\平滑后3.xlsx')#读取数据
height,width = df.shape
print(height,width,type(df))#数据大小
##提取光信息特征
data2=df.iloc[:,0:2048]#光学频率：1-2048
from matplotlib import pyplot as plt
%matplotlib inline
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
x = np.arange(0,2048)
y = np.arange(0,286)
X, Y = np.meshgrid(x, y)
Z = np.array(data2)# 具体函数方法可用 help(function) 查看，如：help(ax.plot_surface)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
ax.set_zlim(0, 25000)
# 设置坐标轴的名称
ax.set_xlabel('Wavelength/nm')
ax.set_ylabel('Frame')
ax.set_zlabel('Intensity/Cd')
plt.show()##绘制折线图
df=pd.read_excel('D:\\1 - 副本.xlsx')#读取数据
height,width = df.shape
print(height,width,type(df))#数据大小
##提取光信息特征
data21=df.iloc[0,3:2051]#光学频率：1-2048
data31=df.iloc[1,3:2051]#光学频率：1-2048
data41=df.iloc[2,3:2051]#光学频率：1-2048
data51=df.iloc[3,3:2051]#光学频率：1-2048df1=pd.read_excel('D:\\平滑后1.xlsx')#读取数据
height,width = df.shape
print(height,width,type(df))#数据大小
##提取光信息特征
data22=df1.iloc[0,0:2048]#光学频率：1-2048
data32=df1.iloc[1,0:2048]#光学频率：1-2048
data42=df1.iloc[2,0:2048]#光学频率：1-2048
data52=df1.iloc[3,0:2048]#光学频率：1-2048
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt#这里导入你自己的数据
#......
#......
#x_axix，train_pn_dis这些都是长度相同的list()#开始画图
# matplotlib其实是不支持显示中文的 显示中文需要一行代码设置字体  
import matplotlib
import matplotlib.pyplot as plt 
mpl.rcParams['font.family'] = 'SimHei'  
plt.rcParams['axes.unicode_minus'] = False   # 步骤二（解决坐标轴负数的负号显示问题）  
matplotlib.rcParams['xtick.labelsize'] =15#x、y轴刻度值大小
matplotlib.rcParams['ytick.labelsize'] =15
matplotlib.rcParams['axes.labelsize'] = 15#x轴、y轴标签值大小
plt.figure(figsize=(12, 12))plt.subplot(2,2,1)
x=np.arange(1,2049,1)plt.title('第一次监测')
plt.plot(x, data21, color='green',label='平滑前')
plt.plot(x, data22, color='red',label='平滑后')plt.legend() # 显示图例plt.xlabel('Wavelength/nm')
plt.ylabel('Intensity/Cd')#python 一个折线图绘制多个曲线
plt.subplot(2,2,2)
plt.title('第二次监测')
plt.plot(x, data31, color='green', label='平滑前')
plt.plot(x, data32, color='red', label='平滑后')
plt.legend() # 显示图例
plt.xlabel('Wavelength/nm')
plt.ylabel('Intensity/Cd')plt.subplot(2,2,3)
plt.title('第三次监测')
plt.plot(x, data41, color='green', label='平滑前')
plt.plot(x, data42, color='red',label='平滑后')
plt.legend() # 显示图例
plt.xlabel('Wavelength/nm')
plt.ylabel('Intensity/Cd')plt.subplot(2,2,4)
plt.title('第四次监测')
plt.plot(x, data41, color='green', label='平滑前')
plt.plot(x, data42, color='red',linestyle='dashed', label='平滑后')
plt.legend() # 显示图例
plt.xlabel('Wavelength/nm')
plt.ylabel('Intensity/Cd')
plt.show()

这篇关于python实现时序平滑算法SG滤波器的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---