数学建模（一）——DVD在线租赁（05年国赛B题）

题目到全国大学生数学建模竞赛网站下载。

在学习阶段的十几年甚至二十多年里，很多时候我们都是在顺向思维地接受知识，但是建模需要我们自己去创造，它要求我们对已学的知识的掌握有很高的灵活度；建模的问题可能很生活化，也可能和物理关联密切，总之它使我们遇到的问题丰富多样，能够提升我们对数学知识的运用能力，使我们真正把数学用起来，而不是一味记忆，认同地积累，积累···

DVD在线租赁是一个很经典的建模题目，主要使用概率知识和整数规划优化模型，题目难度不算太大但很有意思。本博客参考了一份当年获得特等奖（作者是西北工业大学的王颖 高德宏 施恒）的论文（以下直接简称 论文），其中确有很多吸睛亮点使我非常称赞，一眼看出作者们的小脑袋很灵光 ，明白自己和优秀的他们的差距 ，但也当然有一些仔细考察能够发现的瑕疵。

本文只是分析记录自己认为的重点，并不面面俱到，详细求解请参考原论文。

（一）题目梳理

首先把题目梳理清楚，把关键信息提炼出来，做成思维导图，便于分析：

学习建模万不能一上来就看别人的解决方案，这样就又是学习，接受，还是顺向的走完全程，对我们的大脑没有足够的训练，应该自己仔仔细细梳理几遍题目，把条理理顺，然后尽量开动脑子多去想，看自己能想出多少有关的点来，能够想到多深就再也想不下去了，到了自己思考这道题的极限了，可反复思考几遍，感受到山穷水尽已无路，对这道题的难度有个初步评估，再去看别人的论文，你会发现，自己真是挺聪明的，想到的还挺多挺正确，也会发现别人拿特等奖是多么的当之无愧理所应当，你也会感慨这么简单的数学知识自己竟然没有挖掘出来，其实不会灵活运用······这样子，趣味才会浮现出来。

（二）问题一

表1的5种DVD，应分别准备多少张，以保证想看此DVD的会员中，至少50%在1月内能看到
表1的5种DVD，应分别准备多少张，以保证想看此DVD的会员中，至少95%在3月内能看到

看完题目我们知道，必须对偏爱程度，用户满意度进行具体的量化。

其次，我们需要做出必要的假设以简化问题的分析，我认为论文的这几个假设非常合理和必要。

不要觉得建模里假设不重要，实际上假设很能体现出你对问题的分析深度和考察问题的全面性。你可以自己试着提几条你觉得应该写的假设，有可能写不到这几点。
每条假设对于后面的建模求解是非常重要和必须的。

(1)Highlight 1

发现${\xi }_{ij}$服从两点分布
从而发现${\eta }_j$服从二项分布
从而计算出每种DVD需求量的期望值$E({\eta }_j)$。

(2)Highlight 2

在下图的假设后进一步考察了这么假设的可靠程度！！！
这是大多数人所考虑不到的！! !

“要使50%的会员在一月内看到想要的DVD，直接把需求量的期望除以2”这个假设我们都容易想到，我们可能会觉得这个假设有点粗糙，但不知道可以用下面这个计算来求解出这个假设使结论成立的概率，也就是文中所说的可靠程度。

这个计算很简单很好理解，但$P(50\%{\eta }_j\le \frac{1}{2}E({\eta }_j)）$的列出确实甩掉一拨人。

由于50%的可靠度太低，为了提高可靠度，需要对这个购买量假设（需求量的期望除以2，即$\frac{1}{2}E({\eta }_j)$）适当增加，以提高满足结论的可靠程度：

增加的量是：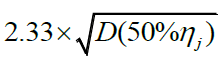
即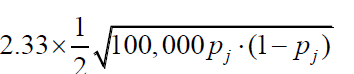

(3)Highlight 3

利用条件“60%的会员每月租2次，40%的会员每月只租1次”进一步缩减DVD的购买量。

作者想到去计算每张DVD的重用期望概率，真是很清奇的思路和角度，值得膜拜。

但我觉得这个亮点相比前两个要暗淡一点，因为

• “一张DVD是第一次被租赁还是第二次被租赁是等可能的”的假设实际上不是很合理，但是题目中无更多信息得到具体概率，算无奈之举。
• 不能通过一张DVD的重用期望概率是0.3就得到“只需要准备所需量的70%”的结论。假设对某张DVD，买了x张，那么就有0.3x张是可以重用的，也就是$x+0.3x=所需量$，所以$x=\frac{所需量}{1.3}\approx 0.77>70\%$,当然差距不大，所以也还好。

对于问题1的第二个小问，一般都是稍微变化第一小问就可以得到答案：

（二）问题二

网站手上现有100种DVD，有1000个会员订单，如何分配可以让会员获得最大的满意度？

问题一只涉及到概率的知识，两点分布，二项分布，标准正态分布的分布函数，期望···

现在问题二就要涉及到优化了。也就是在一定约束下，max或者min某个目标函数的问题

(1)Highlight 1

用了三个矩阵，而不用分量形式，大大简化了模型的表示。

• 分配矩阵，表述了分配方案
  
• 偏爱程度矩阵
  
• 满意度矩阵
  

（2）Highlight 2

把用户满意度进行归一化，即标准化：


最终整数规划模型是：

使用lingo软件求解。

（三）问题三

如果100种DVD现有数量为0，如何采买和分发可以使得1月内95%的会员得到想看的DVD，并且满意度最大？

个人觉得论文对问题三的求解不算好，分两次采买，比较次优吧，先不写，以后看了别的论文的方案再来补充。