本文主要是介绍SMO Algorithm流程,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
SMO Algorithm流程
SMO Algorithm
Input: T T = ,精度 ϵ ϵ
Output:近似解 y^ y ^
1. 取初值 α(0) α ( 0 ) =0, k=0
2.1: 选取最优变量:对于第一个变量 α(k)1 α 1 ( k ) ,遍历所有 0<αi<C 0 < α i < C 的值,也就是 yi∗g(xi)=1 y i ∗ g ( x i ) = 1 的值,也就是支持向量,检验是否满足KKT条件,也就是,是否满足一下三个条件:
∑Ni=1αiyi=0 ∑ i = 1 N α i y i = 0
o≤αi≤C o ≤ α i ≤ C , i=1,2,...,N i = 1 , 2 , . . . , N
yi∗g(xi)≥1,for y i ∗ g ( x i ) ≥ 1 , f o r { { xi| x i | αi=0 α i = 0 } }
yi∗g(xi)=1,for y i ∗ g ( x i ) = 1 , f o r { { xi| x i | 0<αi<C 0 < α i < C } }
yi∗g(xi)≤1,for y i ∗ g ( x i ) ≤ 1 , f o r { { xi| x i | αi=C α i = C } }
其中 g(xi)=∑Nj=1αjyjK(xj,xi)+b g ( x i ) = ∑ j = 1 N α j y j K ( x j , x i ) + b
若不满足,则选取该点,若支持向量全部满足,则遍历其他非支持向量,直到找到不满足该KKT条件为之
对于第一个变量 α(k)2 α 2 ( k ) ,则采用以下策略:
若对于第一个变量 α(k)1 α 1 ( k ) 对应的 E1>0 E 1 > 0 ,则选取使得 E2 E 2 最小的点 ,
若对于第一个变量 α(k)1 α 1 ( k ) 对应的 E1<0 E 1 < 0 ,则选取使得 E2 E 2 最大的点 ,
其目的,使得 αnew2 α 2 n e w 依赖于 E1−E2 E 1 − E 2 , 则去使得 E1−E2 E 1 − E 2 最大(加快计算)的点
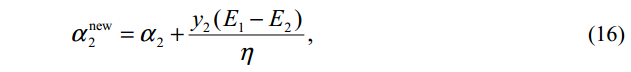
其中 Ei=g(xi)−yi={∑Nj=1αjyjK(xj,xi)+b}−yi E i = g ( x i ) − y i = { ∑ j = 1 N α j y j K ( x j , x i ) + b } − y i
2.2 二次规划求解: 对于选取的第一个变量
其中,原始为剪辑的值为,
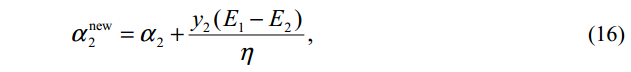
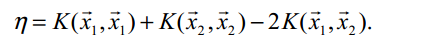
剪辑之后得到第一个变量的解:
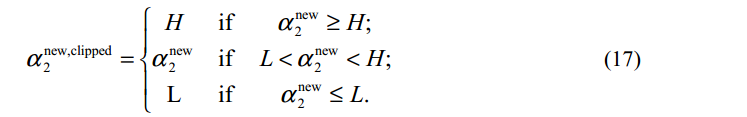
于此同时,由 αold1∗y1+αold2∗y2=ε=αnew1∗y1+αnew,clipped2∗y2 α 1 o l d ∗ y 1 + α 2 o l d ∗ y 2 = ε = α 1 n e w ∗ y 1 + α 2 n e w , c l i p p e d ∗ y 2
可得到第二个变量的解:
αnew1=αold1+y1∗y2(αold2−αnew,clipped2) α 1 n e w = α 1 o l d + y 1 ∗ y 2 ( α 2 o l d − α 2 n e w , c l i p p e d )
基于以上的算法,可以得到最优解 α(k+1)1 α 1 ( k + 1 ) α(k+1)2 α 2 ( k + 1 )
3. 若在精度范围内所有点都满足KKT条件,则跳转(3),否则转(2)
4. 取 α^=α(k+1) α ^ = α ( k + 1 )
这篇关于SMO Algorithm流程的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






