力扣LCR 130. 衣橱整理（DFS 解法）

Problem: LCR 130. 衣橱整理

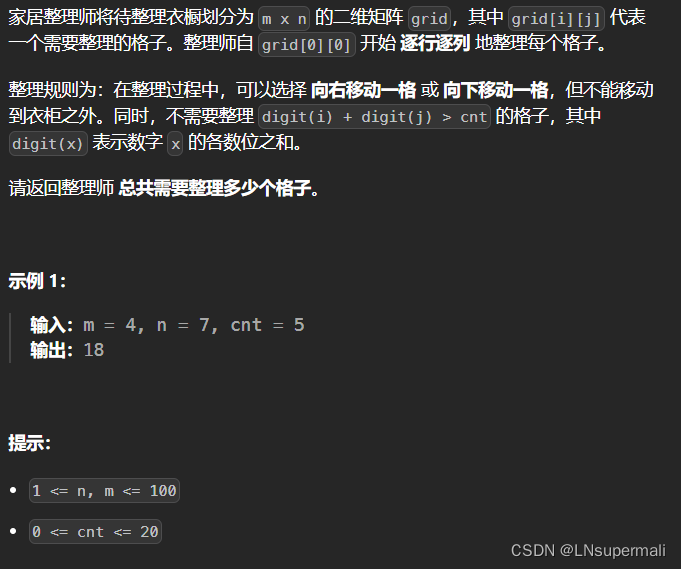
题目描述

思路

首先该问题可以归纳为一类遍历二维矩阵的题目，此类中的一部分题目可以利用DFS来解决，具体到本题目：

我们可以利用一个布尔类型的二维数组记录我们已经访问过的可以访问的位置（访问过则记录为true），再同时在每次遍历时我们判断当前的位置是否可以访问（依据题目要求其横纵坐标的数位和要小于给定的数字cnt），以及当前位置的上、下、左、右四个方位是否可以继续访问。

解题方法

1.定义布尔类型的二维数组（大小为mn）用于记录已经访问过的可以访问的位置。定义int类型的变量count记录可以访问的位置个数；
2.编写判断当前横纵坐标数位和是否大于给定数的函数check；
3.编写深度优先函数:

3.1每次先将当前位置标记为true，count加一
3.1用一个二维数组**int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};记录某个位置的上下左右四个方位的位置，便于DFS，
3.2for循环（从1-4表示查找四个方位），每次执行令newI = i + directions[di][0];newJ = j + directions[di][1];**表示下一个待选位置的横纵坐标
3.3判断下一个待选位置的横纵坐标是否合法（横纵坐标不越界，没有被合法访问过，数位和小于给定数）

复杂度

时间复杂度:

$O(mn)$

空间复杂度:

$O(mn)$

Code

class Solution {private boolean[][] visited;private int count = 0;/*** Get the maximum number of collations** @param m   The maximum range of the horizontal coordinate* @param n   The maximum range of the ordinate* @param cnt Given number* @return int*/public int wardrobeFinishing(int m, int n, int cnt) {visited = new boolean[m][n];dfs(0, 0, m, n, cnt);return count;}/*** Use DFS to get the maximum number of collations** @param i Abscissa* @param j Ordinate* @param m The maximum range of the horizontal coordinate* @param n The maximum range of the ordinate* @param k Given number*/private void dfs(int i, int j, int m, int n, int k) {//Mark the current locationvisited[i][j] = true;count++;//The current position of the location of the four directionsint[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};for (int di = 0; di < 4; ++di) {int newI = i + directions[di][0];int newJ = j + directions[di][1];if (newI >= m || newI < 0 || newJ >= n || newJ < 0|| visited[newI][newJ] == true || check(newI, newJ, k) == false) {continue;}dfs(newI, newJ, m, n, k);}}/*** Determine if the sum of digits is less than k** @param i Abscissa* @param j Ordinate* @param k Given number* @return boolean*/private boolean check(int i, int j, int k) {int sum = 0;while (i != 0) {sum += (i % 10);i /= 10;}while (j != 0) {sum += (j % 10);j /= 10;}return sum <= k;}
}