本文主要是介绍代码随想录Day17:二叉树Part4,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Leetcode 110. 平衡二叉树
讲解前:
这道题其实稍微花了点心思,但是最终想出来解法的时候回过头来看并不是那么麻烦,对于平衡二叉树其实就是一个理念,我们要保证无论是树中的任何一个节点,其左右子树的深度差别不能大于1,所以很显然这是一个递归的问题,遍历所有的root然后去查看他们的高度差,可是原方程返回的是一个Boolean,这样显然没办法帮助我们实现递归,同时子树的高度需要的是一层一层的返回给上面的root,所以高度差这个变量需要被当做递归之外的一个值来更新,然后递归中需要找到的值就被简化为了单纯的当前root的左右子树深度
class Solution:def isBalanced(self, root: Optional[TreeNode]) -> bool:# have a value to keep track of the diffdiff = 0# do a postorder dfs to get the height of each root# and calculate the diff in betweendef dfs(root):nonlocal diffif not root:return 0left = dfs(root.left)right = dfs(root.right)# calculate the diff and keep its max valediff = max(diff, abs(left - right))return 1 + max(left, right)dfs(root)return diff < 2这里我通过全局变量diff来记录每一次遍历中当前root的左右子树深度差,然后递归的返回值只是单纯的当前root的最大深度,其逻辑和求树的最大深度是一样的,这样我们只需要在最后返回diff所记录过的最大值是否存在过大于1就可以了
讲解后:
class Solution:def isBalanced(self, root: Optional[TreeNode]) -> bool:# do a postorder dfs to get the height of each root# and calculate the diff # once we find a root which is not balanced# start returning -1 for all the previous recursiondef dfs(root):if not root:return 0# after we get the value of left and right# check if they are -1 first# if so, meaning previous recursion already found a root that # is not balanced, then simply keep returning -1 to tell the top rootleft = dfs(root.left)if left == -1:return -1right = dfs(root.right)if right == -1:return -1# calculate the diff and keep its max valediff = abs(left - right)if diff > 1:return -1else:return 1 + max(left, right)return dfs(root) != -1这里是听完了卡哥的讲解之后修改过了的代码,其实卡哥和我的主要思路是一样的,这道题归根结底就还是对于每一个root进行当前左右子树最大深度的比较然后来判断是否找到了不平衡,但我一开始的方法是有一个全局变量来保存所有出现过的左右子树最大深度的差,在最后来看最大值是否大于1,但是卡哥有了一个更聪明的办法,就是通过设定-1来作为一个特殊情况的返回值,就是找到了不平衡的树之后,在那后面所有的recursion就不再需要继续计算子树高度之类的了,只需要告诉最上层的root也就是第一个recursive call我们已经找到了一个不平衡的树就可以了,所以就把-1一直return回去就可以
Leetcode 257. 二叉树所有路径
讲解前:
这道题有点麻烦,我还没有开始接触需要进行回溯的算法题,所有我能大概想象出这道题的思路但是我觉得真的写起来肯定会出现很多bug然后花费大量时间,所以我决定这道题就先看一下题解
讲解后:
听完了讲解之后就明白了很多然后我有自己花了图走了一边其中我们是如何记录每一条路径的
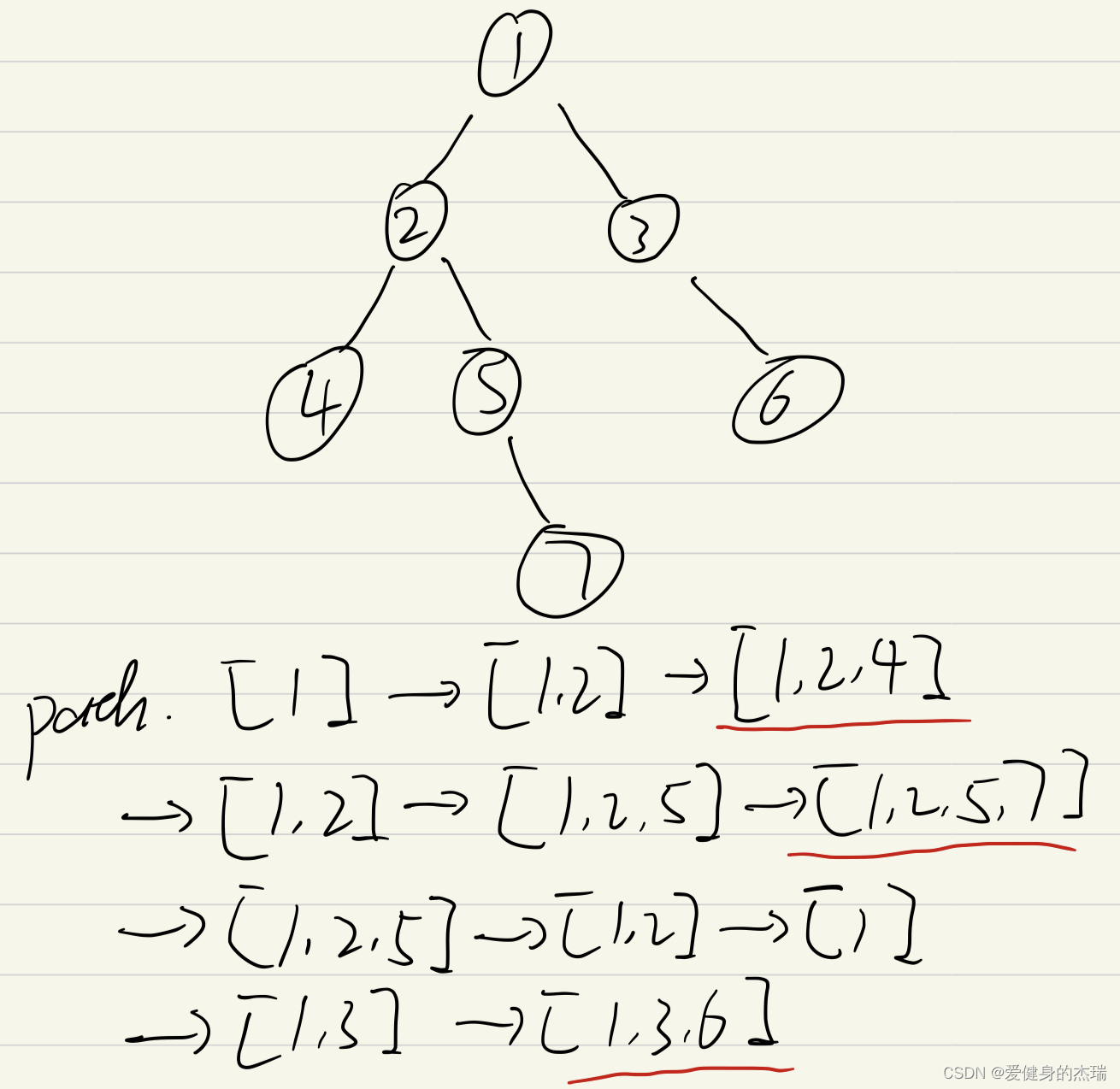
图中的path就是一个变量,是我们递归函数的param,每一次遍历都会传递和更新,他用来记录我们当前经历的路径,并且每当我们发现了一个叶子节点之后,就会把path的值添加到res里面去
这道题因为我们需要记录的当前节点指向下一个节点来一步一步完成一个path,所以要用到前序遍历,然后呢我们的终止条件就设定为当我们当前遍历的node是一个叶子节点时,就return 开始返回递归,在这个过程中其实会发生两件事,第一件就是在base case中,我们会把这时的path转化为题目要求的 '1->2->4' 的箭头连接字符串形式然后添加到result列表中,再然后就是直到我们返回到一个还没有call 他右边的root.right 的recursive call的节点之前,我们其实simply一直在做path.pop() 的操作,让path中存放的路径开始退回到一个能开始新路径的节点
class Solution:def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:path = []res = []if not root:return resdef dfs(root, path, result):# add the value first in case we find leaf node aferpath.append(root.val)# base case if we find root or notif not root.left and not root.right:temp = '->'.join(map(str, path))res.append(temp)return# recursive case, check if left or right not null firstif root.left:dfs(root.left, path, result)# after we finish a call which means we reached the leaf node# start pop back up until we got back to the root where is a # right node leads to a path we havent gone topath.pop()if root.right:dfs(root.right, path, result)# also pop back uppath.pop()dfs(root, path, res)return resLeetcode 404. 二叉树的左叶子之和
讲解前:
这道题用到的方法可以说是后序遍历但是其实在处理环节我们没做任何的事情,对于递归的思路中这道题的base case很好理解,那就是当我们找到一个叶子节点之后就可以返回了,并且这个时候应该把这个叶子的val加入到sum中去,如果这个叶子是一个root的左节点,那么唯一问题就是如何判断是不是root的左节点呢,其实我就对我们的函数多加了一个Boolean的值,每当我们当前的节点是通过其root节点的dfs(root.left) 的call来遍历到的,那么我们就知道他是root的左节点,那么我们就同时也传入一个True
class Solution:def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:sum_ = 0def dfs(root, is_left):nonlocal sum_if not root.left and not root.right and is_left:sum_ = sum_ + root.valif root.left:dfs(root.left, True)if root.right:dfs(root.right, False)dfs(root, False)return sum_讲解后:
看完了卡哥的讲解之后发现思路其实和我的不太一样,卡哥的代码中其实一直很遵循递归的前中后序的原则,然后其实这道题也是先把问题小化就是每个节点其实都是可以求他的左叶子节点的和的,root在左右节点不是叶子也无所谓,就继承之前的值就可以了通过递归的return
class Solution:def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:if not root or (not root.left and not root.right):return 0left = self.sumOfLeftLeaves(root.left)if root.left and not root.left.left and not root.left.right:left = root.left.valright = self.sumOfLeftLeaves(root.right)return left + right这篇关于代码随想录Day17:二叉树Part4的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






