LeetCode103. 二叉树的锯齿形层序遍历

本文主要是介绍LeetCode103. 二叉树的锯齿形层序遍历，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

---

解决思路：
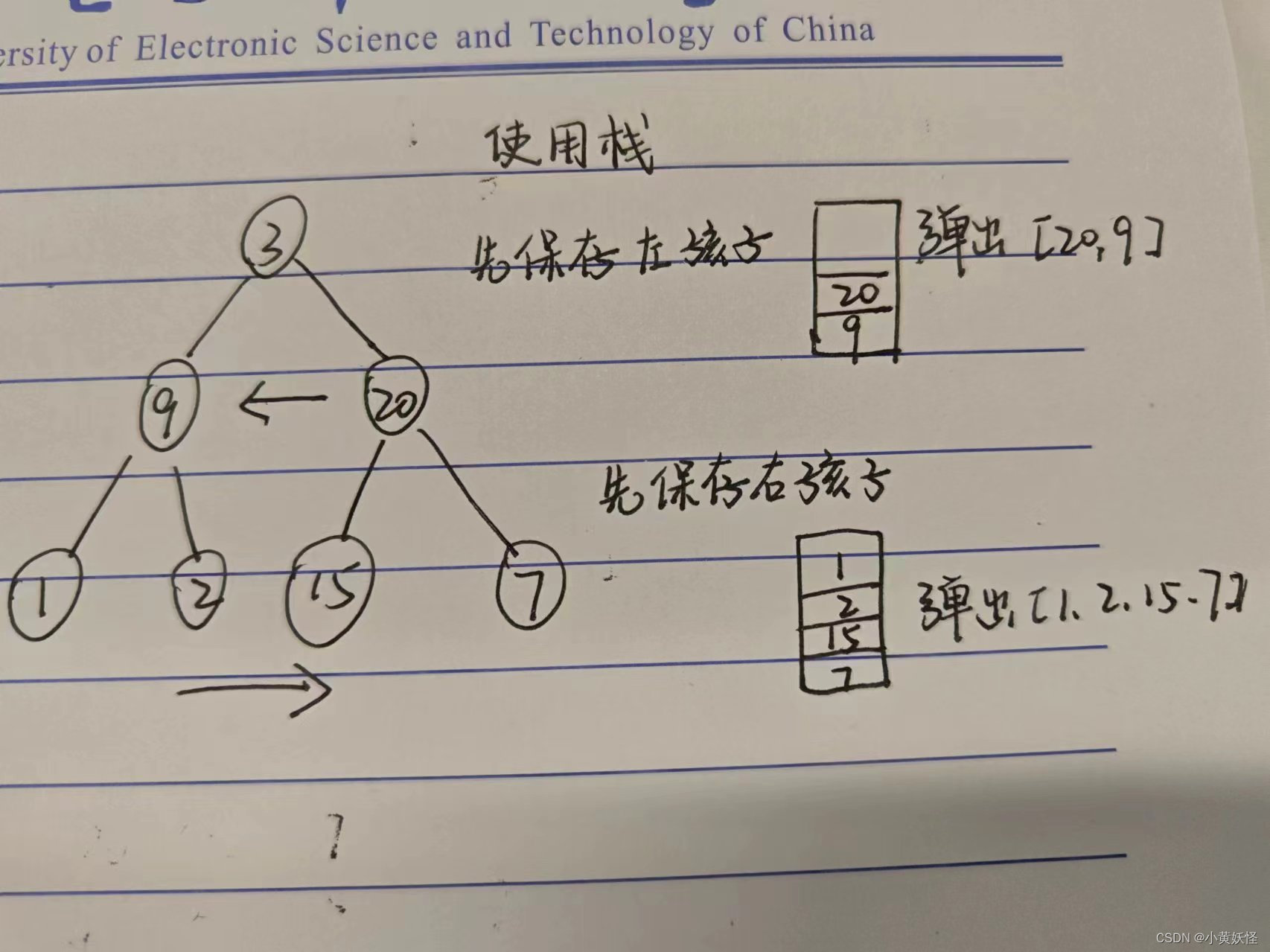
使用两个栈来实现功能，一个全局栈global，一个局部栈temp，此外设置一个标志位label来判断在每一层时保存孩子的顺序
使用全局栈来进行遍历输出节点，在输出的同时将左右孩子节点存入局部栈中。
当每一层遍历完毕之后，将局部栈克隆给全局栈，此时全局栈具有下一层的节点。
每当遍历一层之后，更换保存孩子的顺序，如下图所示：
由于需要遍历节点，所以时间复杂度为O（n）
代码如下：

package 二叉树;import java.util.*;public class LeetCode103二叉树的锯齿层序遍历 {public static class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val,  TreeNode left,  TreeNode right) {this.val = val;this.left = left;this.right = right;}}public static void main(String[] args){TreeNode root=new  TreeNode(3);TreeNode node1=new  TreeNode(9);TreeNode node2=new  TreeNode(20);TreeNode node3=new  TreeNode(15);TreeNode node4=new  TreeNode(7);TreeNode node5=new  TreeNode(2);TreeNode node6=new  TreeNode(1);root.left=node1;root.right=node2;node2.left=node3;node2.right=node4;node1.right=node5;node1.left=node6;//定义层序遍历List<List<Integer>> result=new ArrayList<>();//使用栈Stack<TreeNode> global=new Stack<>();global.push(root);int label=0;while(!global.isEmpty()){int size=global.size();List<Integer> temp_list=new ArrayList<>();Stack<TreeNode> temp_stack=new Stack<>();for(int i=0;i<size;i++){TreeNode child=global.peek();global.pop();temp_list.add(child.val);if(label==0){if(child.left!=null) temp_stack.push(child.left);if(child.right!=null) temp_stack.push(child.right);}else{if(child.right!=null) temp_stack.push(child.right);if(child.left!=null) temp_stack.push(child.left);}}//将temp_stack中的对象克隆给globalglobal= (Stack<TreeNode>) temp_stack.clone();temp_stack.clear();result.add(temp_list);if(label==0){label=1;continue;}if(label==1){label=0;}}System.out.println(result);}}

这篇关于LeetCode103. 二叉树的锯齿形层序遍历的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---