12枚硬币称量问题——矩阵学习笔记

问题：有12枚硬币，至多有一枚质量不同的假币。有一座天平，有3次称量机会，解决以下问题：

      1.是否有假币？

      2.如果有假币，它的编号是多少？

      3.如果有假币，它比普通的硬币轻和重

思路：矩阵；提前设计好每一步的称量方案，先收集每次称量的结果，再用处理方法把称量结果转化成和假币有关的信息；编码+查列

核心：编码论中的校验矩阵。校验矩阵的原理：作用在一条经过编码的信息上，由校验结果能够确定其中是否有噪声引起的错误，设计得当还可以定位并纠错。在该题中，称量矩阵充当了校验矩阵，硬币的质量是输入的信息，称量结果则用来差错与纠错。

     其实硬币称量问题和平衡三进制紧密相关，虽然二者在运算细节上稍有差异，但是两个框架下的问题依然可以相互转化，答案也能够彼此借鉴。

1.将称量用数学来描述：用 “m1，m2，m3，……”来代表对应编号的硬币的质量，将“*（-1）“代表放在左盘，将“*1”代表放在右盘，将“0”代表不加入称量。那么一次称量可以转换为“（-1）*m1+(-1)*m2+(-1)*m3+(-1)*m4+1*m5+1*m6+1*m7+1*m8+0*m9+0*m10+0*m11

+0*m12”，改变称量方式，只需要改变相应的系数。当天平平衡，该式等于0；当天平向左倾斜，该式小于0；当天平向右倾斜，该式大于0。各项系数反映硬币的摆放情况，计算结果反映称量后天平的状态。

2.将系数整理成行向量，硬币质量整理成列向量，转换为矩阵乘法的形式。如图：

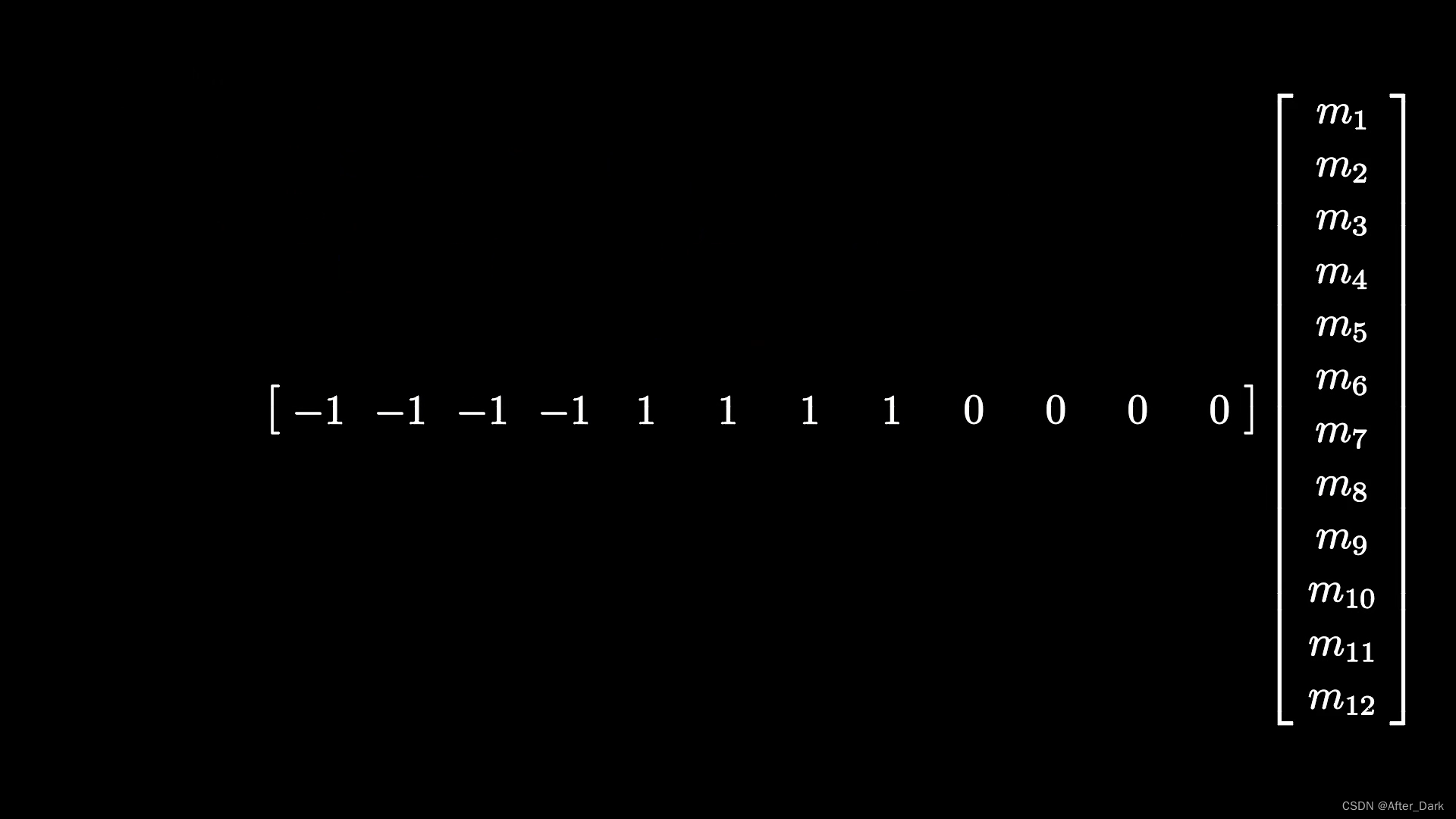
在多次称量的情况下，代表质量的列向量彼此相同，所以包含系数的行向量可以整合起来，形成一个矩阵。如图：

其中第n行对应第n次称量，第n列对应n号硬币。相应的，矩阵乘法的结果也是一个向量，第n个元素对应第n次称量的结果，”1”代表“向右倾斜”，“0”代表“平衡”，“-1“代表”向左倾斜“如图：

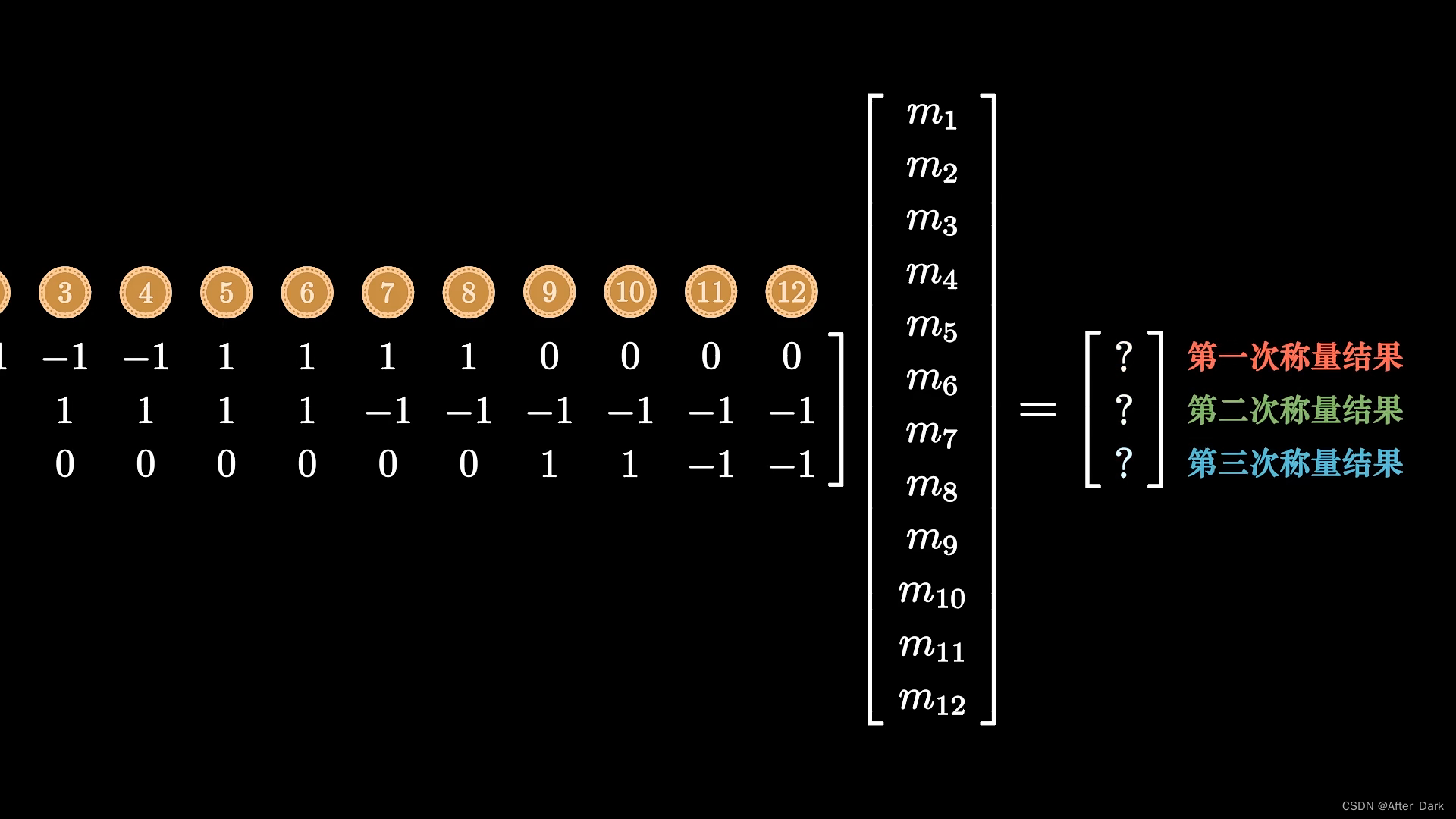
将左边的叫“称量矩阵“，右边的叫”结果向量“，中间的叫”质量向量“。质量向量的12个元素还可以继续拆分成两项，一项是真币的质量m，称为“标准向量”，一项是硬币的偏差值”b1，b2，b3……”，称为“偏差向量”。真币的偏差值为0，偏轻的假币的偏差值用-1表示，偏重的硬币的偏差值用1表示。最后转换为如图的形式：

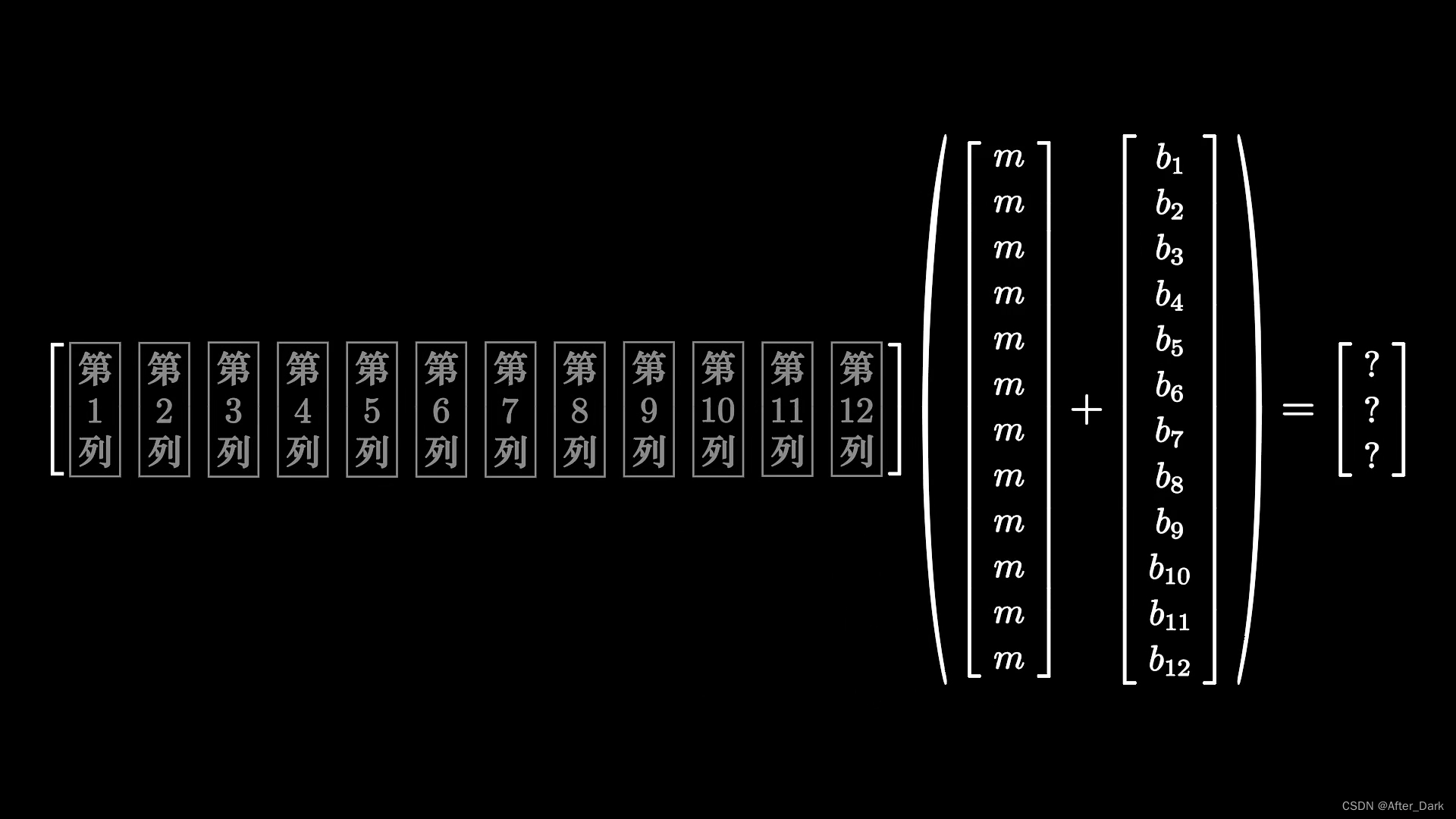
用天平称量就是在“质量向量”前乘上“称量矩阵”，称量的结果就是“结果向量”。我们需要通过“称量矩阵”得到“结果向量“，再借助“结果向量”去反推“偏差向量”。

3.称量矩阵是作用在标准向量和偏差向量上的，因为m是一个未知的常数，所以标准向量处理起来比较麻烦，因此进行“归零”，也就是让称量矩阵与标准向量的乘积是零向量。根据矩阵乘法进行转换可得出如图的式子：

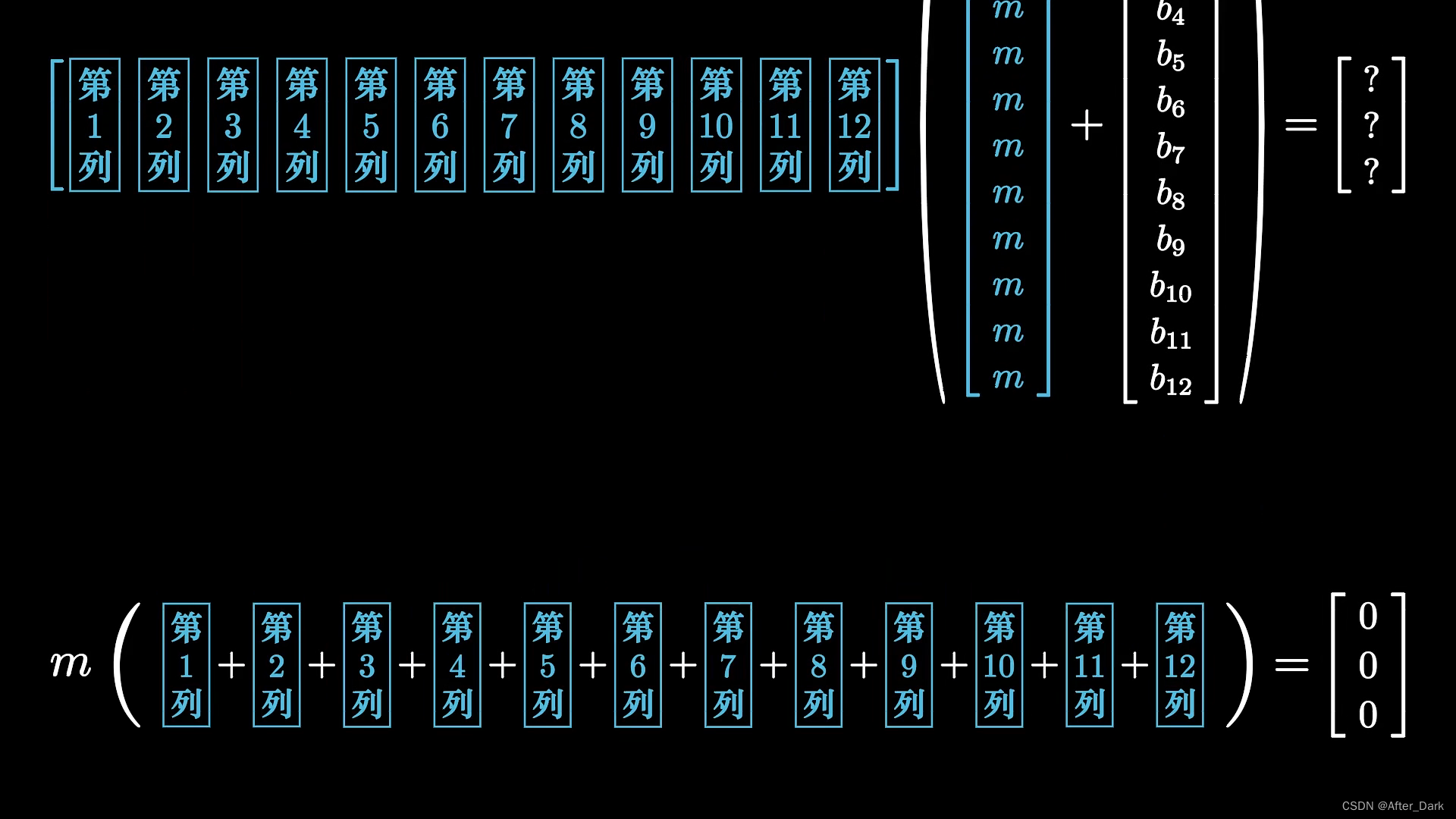
按照矩阵乘法要实现“归零”，需要让称量矩阵每一行元素的和是零，满足这个条件，标准向量就不再产生影响，可以去掉，得到如图的式子：

    当所有硬币是真的，那么偏差向量就是零向量，因此结果向量也始终是零向量。当某个硬币是假币时，那么它的编号所对应的偏差向量中的元素不是0，那么当称量矩阵与它作用时，只有它所对应的称量矩阵中的一列能够保留下来。假币如果偏重，那么它的编号所对应的偏差向量中的元素就是“+1“，留下来的是正的一列，同理，假如假币偏轻则是”-1“，留下来的是负的一列。所以结果总是称量矩阵的其中一列，或者是负的其中一列，加上没有假币时的零向量。一种有25种可能。

4.这样就知道了称量矩阵的要求，第一，零向量单独出现，所以称量矩阵不能出现全零的列。第二，任意两列不同，可以避免不必的额外的称量。第三，任意两列的和不为零向量，因为假如-a列与b列相同，那么假币为b列所对应的硬币且假币偏重时，无法判断假币究竟是偏轻的a币还是偏重的b币。满足这三个条件，可以保证25个结果向量必然不同，也就能实现从结果反推偏差的初衷了。

   除此之外，还要额外加两个条件：第四，称量矩阵本身的元素只能是-1、0或1；第五，每一行的元素和为0（为了实现“归零“以此消掉m）。同时满足五个条件，称量矩阵就是合适的，可以实现通过结果去反推偏差的需求。

然后就可以设计称量矩阵了，先排列出满足“元素只能是-1、0或1“的要求的列，除去零向量，还剩26列。将26列分为两组，每一组的两个向量的和为零向量，每一组最多只选1个向量作为列就可以满足“任意两列的和不为零向量”的条件。可以通过修改挑选的组（选出13列，只需12列，多出一列）和每组挑选的向量来解决“每一行的和为0”的条件。首先让第一行的和为0，然后在保证第一行和不变的条件下调整第二行的和为0，以此类推。

5.在经过计算后，由得出的“结果向量“去“称量矩阵“找到对应的列或对应的负的列，该列的编号就是假币的编号。如图，得到的结果向量是负的第5列，所以5号是偏轻的假币。

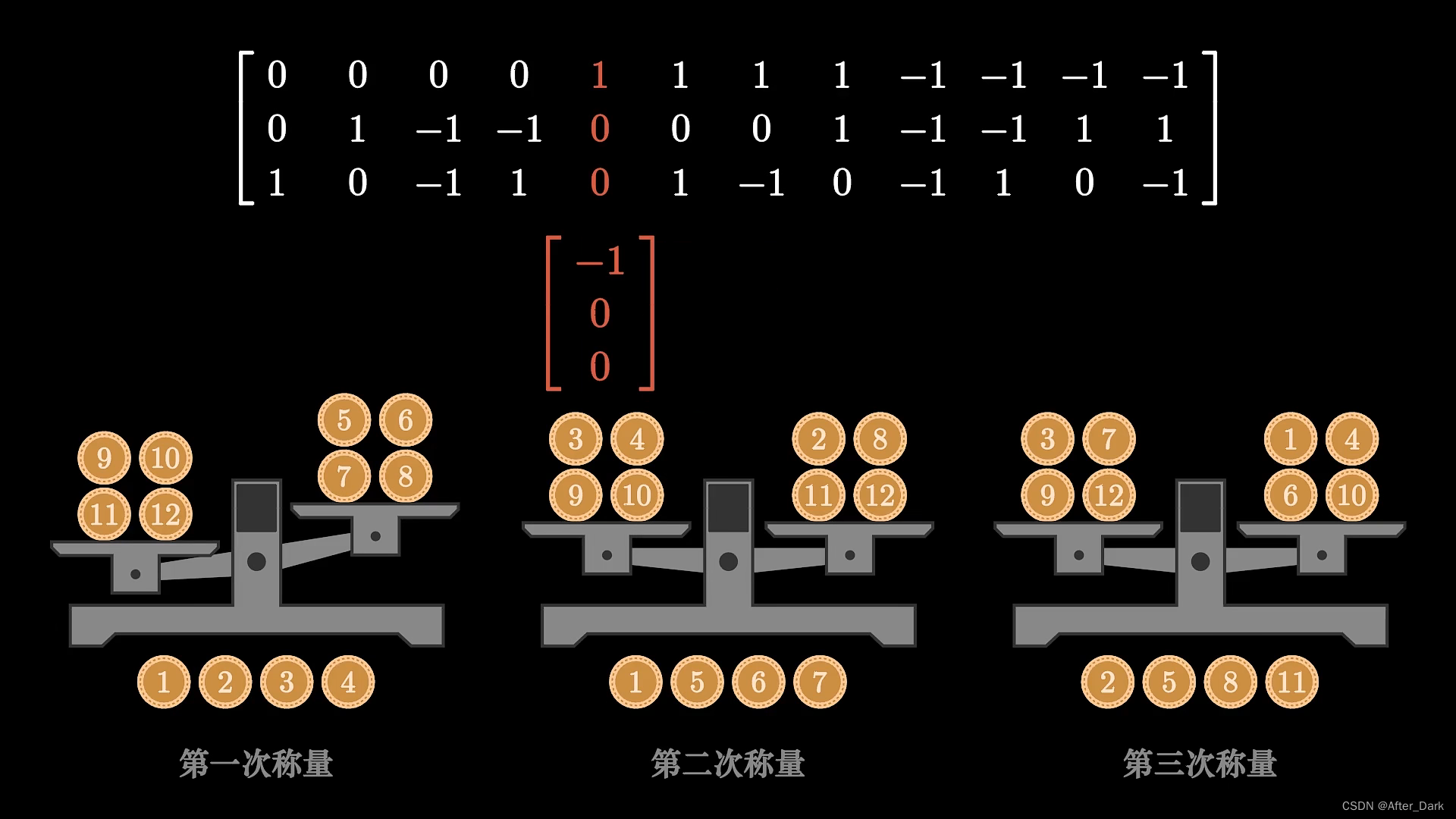
如果得到的是零向量，那么硬币都是真的。