阶乘的强悍溢出技能

本文主要是介绍阶乘的强悍溢出技能，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【题目描述】

输入n，计算S＝1！＋2！＋3！＋…＋n！的末6位（不含前导0）。，n！表示

前n个正整数之积。

【样例输入】

【样例输出】

37913

一、阶乘溢出性能体验

按正常逻辑，本题可以分三步：

①求1-n的阶乘。

②把每项阶乘加起来。像这样一项一项地把各个式子加到一起，就是累加器。

③取和的末6位。

但是别忘了还有一个条件：。

一看到这么大的数，又是阶乘，免不了心里一沉，直觉冥冥中指引恐怕long long型也罩不住。

先拿求n的阶乘探探底。

#include<stdio.h>
int main(){for(int n=1; n<=1e6; n++){long long factorial = 1;for(int i=1; i<=n; i++){factorial *= i;}printf("%d %lld\n", n, factorial);}return 0;
}

结果输出一堆0，肯定是鸟鸣山一样，完鸟。

把1e6改成100，仍然是一堆0，看来早就超限了。

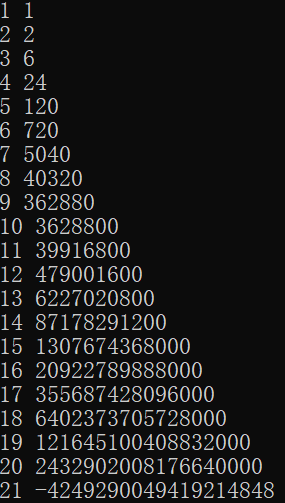
没错，21！的已经输出负数，阶乘的溢出能力实在是太强悍了。

也就是说，用long long型只能计算到20！。如果用int型呢，只能计算到12！。

这可咋办？

二、大数取余神药

据说有一味神药：要计算只包含加法、减法和乘法的整数表达式除以正整数n的余数，可以在每步计算之后对n取余，结果不变。

也就是说：

t=(a*b+c-d)%n中t的值可以分步取余求出：

t1=a*b/%n;
t2=(t1+c)%n;
t=(t2-c)%n;

是何道理呢？其实很简单，因为任何整数除以n的余数都是这个数减去n的倍数后余下的数。

如果x%n=y，它的意思是x=kn+y（x、y、k为整数，y<x）。

显然，所有含n的项都能被n整除，不会产生余数，所以可将其去除，变为：

它们分别是a、b、c、d除以n的余数，所以有：

三、代码实现

在神药的帮助下，本题可改为如下两步：

①求1-n的阶乘。用for循环实现累乘，每执行一次乘法都对1e6取余。

②把每项阶乘加起来。用for循环实现累加，每加一次都对1e6取余。

代码如下：

#include<stdio.h>
int main(){const int MOD = 1e6;int n, S = 0;scanf("%d", &n);for(int i = 1; i <= n; i++){int factorial = 1;for(int j = 1; j <= i; j++)factorial = factorial * j % MOD;S = (S + factorial) % MOD;}printf("%d\n", S);return 0;
}

将1e6定义为MOD常量可以改善程序的可读性，也便于修改（代码中有两次用到这个数，使用MOD表示的情况下，如需修改只需改一次MOD的值）。

另一点需要注意的是，两行取余代码千万不要写成下面这种牛皮plus形式：

factorial *= j % MOD;
S += factorial % MOD;

因为*=、+=这种赋值运算符和=一样，优先级是非常低的，而%的优先极和*、/是一样的，所以会先计算取余，再进行乘赋值、加赋值。

比如下面的代码：

#include<stdio.h>
int main(){int i=10;i *=50+2;printf("%d\n", i);return 0;
}

它的结果是520，而不502。

三、代码优化

前面给出的求阶乘之和的代码可以进一步优化，将两层循环减少为一层循环。

如果读到这里，请别急着往下读，先自己思考一下方法。

原理很简单：n！可表示成前n个正整数之积，也可以表示成(n-1)!*n，所以只要保留上一次循环求得的阶乘，就可以通过累乘的方式求得n的阶乘。这时候就要把factorial这个变量放到循环体之外定义。

代码如下：

#include<stdio.h>
int main(){const int MOD = 1e6;int n, factorial=1, S = 0;scanf("%d", &n);for(int i = 1; i <= n; i++){factorial = factorial * i % MOD;S = (S + factorial) % MOD;}printf("%d\n", S);return 0;
}

四、耗时测试

阶乘，最大的阶乘，阶乘之和。这样的豪华的阵容吞噬时间的能力必然很是强悍吧！

如果想了解代码的运行时间，可以用计时函数clock（）。它定义在< time.h>头文件中，该函数返回从程序启动到调用 clock() 时的 CPU 时间。从这个描述咱们要明白：

①统计时间从启动程序开始。这意味着，输入数据的时间也是计算在内的。

②返回时间与clock()代码放置位置有关。

③返回的不是秒数。

针对上述特点，如果咱们想获取程序的纯运行时间（不计用户输入时间），可以采用如下对策：

(1) 借助命令行工具刨除数据输入时间。

①同时按下Win+R键，快速打开运行窗口。

②在运行窗口中输入“cmd”并按回车，打开命令行窗口。

③直接在光标处输入编译后的可执行文件所在盘符，如D：。

④输入cd folder1\folder2（表示D:\folder1\folder2，指程序执行文件所在路径，可以通过复制粘贴的方式输入）

⑤确认进入程序所在路径，然后输入：echo 52|u。操作系统会自动把52输入，其中u是程序名。如果要输入多条数据，可以写成echo 52 92|u。

(2) 计时函数clock( )放在程序结束之前。这样就能返回整个程序的执行时间。

(3) 返回秒数：用clock( )/CLOCKS_PER_SEC可以得到秒数。可以想象有个法号叫CPU的和尚在敲钟，clock( )能告诉你它敲了多少下，CLOCKS_PER_SEC指的是敲钟的速度（每秒敲多少下），二者相除就得到敲了多少秒。

代码如下：

#include<stdio.h>
#include<time.h>
int main(){const int MOD = 1e6;int n, S = 0;scanf("%d", &n);for(int i = 1; i <= n; i++){int factorial = 1;for(int j = 1; j <= i; j++)factorial = (factorial * j % MOD);S = (S + factorial) % MOD;}printf("%d\n", S);printf("Time used = %.2f\n", (double)clock() / CLOCKS_PER_SEC);return 0;
}

将优化前后的代码分别测试结果如下：

n	18	19	20	21	22	23	24	25	26
答案	348313	180313	820313	260313	940313	580313	940313	940313	940313

n	1600	3200	6400	12800	25600	51200	102400	204800	409600
答案	940313	940313	940313	940313	940313	940313	940313	940313	940313
优化前时间	0.03	0.05	0.12	0.38	1.44	5.74	23.28	93.43	381.62
优化后时间	0.03	0.03	0.03	0.03	0.03	0.03	0.03	0.03	0.03