代码随想录刷题day29｜非递减子序列全排列全排列II

本文主要是介绍代码随想录刷题day29｜非递减子序列全排列全排列II，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

day29学习内容

day29主要内容

• 非递减子序列
• 全排列
• 全排列II

---

声明
本文思路和文字，引用自《代码随想录》

一、非递减子序列

491.原题链接

1.1、代码-错误写法

class Solution {List<List<Integer>> result = new ArrayList();List<Integer> path = new ArrayList();public List<List<Integer>> findSubsequences(int[] nums) {backTracking(nums, 0);return result;}private void backTracking(int[] nums, int startIndex) {// 终止条件if (path.size() >= 2) {result.add(new ArrayList(path));return;}// 用一个set判断是否已经使用过HashSet<Integer> set = new HashSet<>();// 遍历for (int i = startIndex; i < nums.length; i++) {// 如果递归时下一层节点的值比子序列最后一个元素值大，不满足递增，所以要返回// 或者之前已经使用过该元素if (!path.isEmpty() && nums[i-1] > nums[i] || set.contains(nums[i])) {continue;}// 单层递归逻辑path.add(nums[i]);set.add(nums[i]);// 递归backTracking(nums, i + 1);// 回溯path.remove(path.size() - 1);}}
}

这种写法有2个地方都是错误的。

1.1.1 多了一个return语句。

if (path.size() >= 2) {result.add(new ArrayList(path));return;}

目的是找到所有可能的递增子序列：目标是列出所有可能的递增子序列，而不仅仅是找到第一个满足条件的子序列后就停止。因此，在找到一个有效子序列并将其添加到结果集后，不应该立即返回，而应该继续探索其他可能的子序列。直接返回会导致漏掉其他有效的子序列组合。

回溯算法的工作机制：在执行回溯算法时，每一次递归调用代表探索决策树的一个分支。当达到一个终结点（即满足特定条件的点）时，我们会记录下当前的路径作为结果之一，然后通过回溯（撤销最后的选择）返回到前一个状态，继续探索其他可能的分支。如果在添加结果后立即返回，那么就会错过从当前点出发的其他潜在路径。

1.1.2、nums[i-1] > nums[i]，这个条件写错了，为什么呢？

注意看老师画的图，是递归的时候比较的。即下一层节点的值比子序列最后一个元素值大，如果比之前的大，就不满足递增了。
确实，针对解释原因2和3，使用数组[3, 4, 1, 5]作为例子可能会更加合适和清晰。这里我们使用这个数组来重新说明原因2和3，以展示为何不应使用nums[i-1] > nums[i]作为判断条件。

1. 忽略了回溯算法的动态决策过程

• 例子：考虑数组[3, 4, 1, 5]。
  • 在进行到4之后，下一个元素是1。如果使用nums[i-1] > nums[i]即4 > 1作为理由停止当前探索，那么我们将错过以1作为起始点、且包含5的递增子序列[1, 5]。
  • 这个例子展示了即使当前元素相对于前一个元素是递减的，它仍然可能是未来某个有效递增子序列的起点。

2. 限制了可能的递增子序列的探索

• 例子：同样考虑数组[3, 4, 1, 5]。
  • 如果我们在遍历到4后面的1时，仅因为4 > 1就停止探索，那么我们不仅错过了以1开始的递增子序列，还错过了整个数组中存在的一个非常明显的递增子序列[3, 4, 5]。
  • 正确的逻辑应该是，即使1相对于4是递减的，我们仍然继续探索，因为1后面的5可以与数组中的其他元素（如3和4）形成有效的递增子序列。

1.2、代码-正确写法

class Solution {List<List<Integer>> result = new ArrayList();List<Integer> path = new ArrayList();public List<List<Integer>> findSubsequences(int[] nums) {backTracking(nums, 0);return result;}private void backTracking(int[] nums, int startIndex) {// 终止条件if (path.size() >= 2) {result.add(new ArrayList(path));}// 用一个set判断是否已经使用过HashSet<Integer> set = new HashSet<>();// 遍历for (int i = startIndex; i < nums.length; i++) {// 如果递归时下一层节点的值比子序列最后一个元素值大，不满足递增，所以要返回// 或者之前已经使用过该元素if (!path.isEmpty() && path.get(path.size() - 1) > nums[i] || set.contains(nums[i])) {continue;}// 单层递归逻辑path.add(nums[i]);set.add(nums[i]);// 递归backTracking(nums, i + 1);// 回溯path.remove(path.size() - 1);}}
}

二、全排列

46.原题链接

2.1、科普

[1,2]和[2,1]是同一个排列

2.2、错误写法

class Solution {List<List<Integer>> result = new ArrayList();List<Integer> path = new ArrayList();public List<List<Integer>> permute(int[] nums) {backTraking(nums);return result;}private void backTraking(int nums[]) {if (path.size() > nums.length) {return;}if (path.size() == nums.length) {result.add(new ArrayList(path));}for (int i = 0; i < nums.length; i++) {path.add(nums[i]);// 递归backTraking(nums);path.remove(path.size() - 1);}}
}

• 为什么是错的
• 
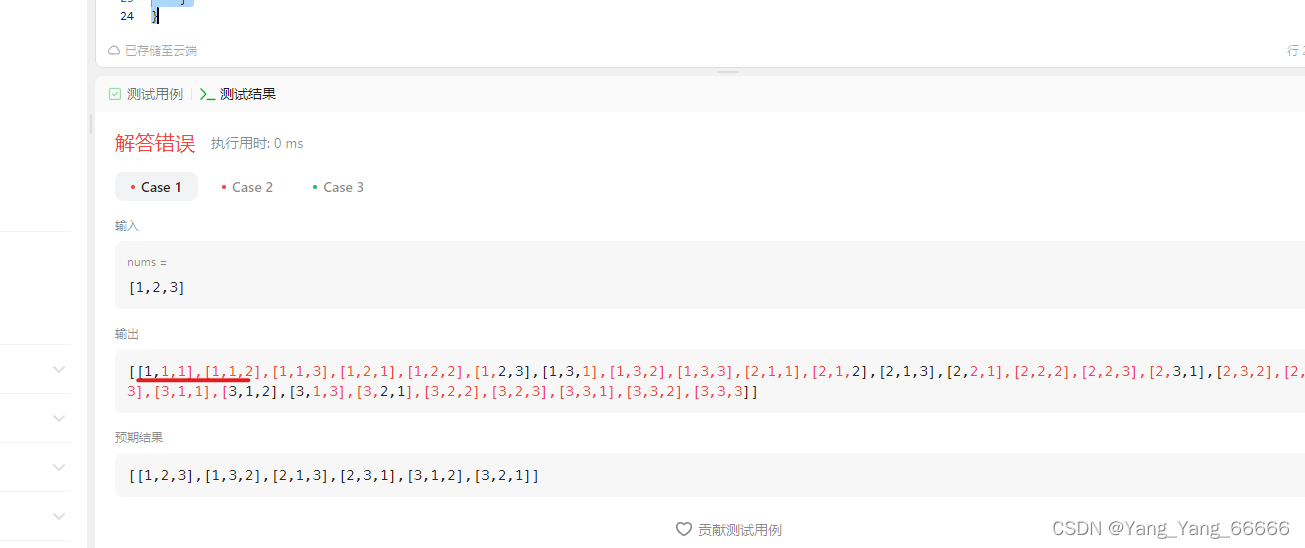
  看图很明显了，有重复数据，没有进行去重。

2.3、正确写法1

class Solution {List<List<Integer>> result = new ArrayList();List<Integer> path = new ArrayList();//用数组标识是否使用过boolean[] used;public List<List<Integer>> permute(int[] nums) {// 初始化数组used = new boolean[nums.length];backTraking(nums);return result;}private void backTraking(int nums[]) {if (path.size() > nums.length) {return;}if (path.size() == nums.length) {result.add(new ArrayList(path));}for (int i = 0; i < nums.length; i++) {if (used[i]) {continue;}path.add(nums[i]);used[i] = true;// 递归backTraking(nums);used[i] = false;path.remove(path.size() - 1);}}
}

三、全排列II

47.原题链接

3.1、思路

• 看麻了，代码抄的题解
• 简单的说，就是在46题的基础上，加了一个去重的逻辑。
• 回溯逻辑（backTraking方法）
• 终止条件：如果path的大小与nums数组的长度相同，意味着已经找到了一个完整的排列，将其添加到result中，并返回。
• 循环和选择：遍历每个元素，尝试将其添加到当前路径（path）中。
• 去重判断：if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) { continue; }
  • 这个条件是去重的核心逻辑。当前元素与前一个元素相同，且前一个元素还未被使用（意味着是在回溯的过程中，而不是在向下构建路径的过程中），则跳过当前元素。
    • 这是因为在这种情况下，选择当前元素会产生与之前处理过的元素相同的排列，从而导致重复。
  • 未使用的元素：如果当前元素未被使用，则将其添加到路径中，并标记为已使用，然后递归地继续构建排列，之后撤销这一选择以尝试其他选项。
• 回溯的撤销操作
  • 在递归调用返回后，执行撤销操作：从路径中移除最近添加的元素，并将used[i]重新标记为false。这一步是回溯算法的典型做法，它确保了在探索完一个元素所有可能性之后，能够正确地恢复状态，并探索下一个元素的所有可能性。

3.2、代码-正确写法

class Solution {List<List<Integer>> result = new ArrayList();List<Integer> path = new ArrayList();// 用数组标识是否使用过boolean[] used;public List<List<Integer>> permuteUnique(int[] nums) {// 初始化数组used = new boolean[nums.length];Arrays.sort(nums);backTraking(nums);return result;}private void backTraking(int nums[]) {if (path.size() == nums.length) {result.add(new ArrayList(path));return;}for (int i = 0; i < nums.length; i++) {if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;}if (used[i] == false) {path.add(nums[i]);used[i] = true;// 递归backTraking(nums);used[i] = false;path.remove(path.size() - 1);}}}
}

看麻了这一题。。

总结

1.感想

• 马上就是连续刷题一个月了，加油。

2.思维导图

本文思路引用自代码随想录，感谢代码随想录作者。

这篇关于代码随想录刷题day29｜非递减子序列全排列全排列II的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---