二叉树18：路径总和两道题

 接下来我通过详细讲解如下两道题，来看看函数返回值的设置问题。其实这个问题也可以归类到nSum问题。但是与二叉树结构更为密切，我们在这里分析更合适。

112. 路径总和

113. 路径总和II

1.LeetCode 112 路径总和

题意：给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目 标和。

说明: 叶子节点是指没有子节点的节点。给定如下二叉树，以及目标和 sum = 22，

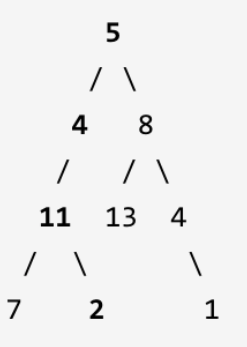
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

1.1 广度优先搜索
 

首先我们可以想到使用广度优先搜索的方式，记录从根节点到当前节点的路径和，以防止重复计算。这样我们使用两个队列，分别存储将要遍历的节点，以及根节点到这些节点的路径和即可。

class Solution {public boolean hasPathSum(TreeNode root, int sum) {if (root == null) {return false;}Queue<TreeNode> queNode = new LinkedList<TreeNode>();Queue<Integer> queVal = new LinkedList<Integer>();queNode.offer(root);queVal.offer(root.val);while (!queNode.isEmpty()) {TreeNode now = queNode.poll();int temp = queVal.poll();if (now.left == null && now.right == null) {if (temp == sum) {return true;}continue;}if (now.left != null) {queNode.offer(now.left);queVal.offer(now.left.val + temp);}if (now.right != null) {queNode.offer(now.right);queVal.offer(now.right.val + temp);}}return false;}
}

 1.2 递归方式

观察要求我们完成的函数，我们可以归纳出它的功能：询问是否存在从当前节点 root 到叶子节点的路径，满足其路径和为 sum。

假定从根节点到当前节点的值之和为 val，我们可以将这个大问题转化为一个小问题：是否存在从当前节点的子节点到叶子的路径，满足其路径和为 sum - val。

不难发现这满足递归的性质，若当前节点就是叶子节点，那么我们直接判断 sum 是否等于 val 即可（因为路径和已经确定，就是当前节点的值，我们只需要判断该路径和是否满足条件）。若当前节点不是叶子节点，我们只需要递归地询问它的子节点是否能满足条件即可。 

class Solution {public boolean hasPathSum(TreeNode root, int sum) {if (root == null) {return false;}if (root.left == null && root.right == null) {return sum == root.val;}return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);}
}

2.LeetCode113 路径总和

与上面的不同之处就是这里要找出所有的路径，并输出。

我们同样可以有深度优先搜索和递归两种方式：

2.1 深度优先

我们可以采用深度优先搜索的方式，枚举每一条从根节点到叶子节点的路径。当我们遍历到叶子节点，且此时路径和恰为目标和时，我们就找到了一条满足条件的路径。

class Solution {List<List<Integer>> ret = new LinkedList<List<Integer>>();Deque<Integer> path = new LinkedList<Integer>();public List<List<Integer>> pathSum(TreeNode root, int targetSum) {dfs(root, targetSum);return ret;}public void dfs(TreeNode root, int targetSum) {if (root == null) {return;}path.offerLast(root.val);targetSum -= root.val;if (root.left == null && root.right == null && targetSum == 0) {ret.add(new LinkedList<Integer>(path));}dfs(root.left, targetSum);dfs(root.right, targetSum);path.pollLast();}
}

 2.2 广度优先

我们也可以采用广度优先搜索的方式，遍历这棵树。当我们遍历到叶子节点，且此时路径和恰为目标和时，我们就找到了一条满足条件的路径。

为了节省空间，我们使用哈希表记录树中的每一个节点的父节点。每次找到一个满足条件的节点，我们就从该节点出发不断向父节点迭代，即可还原出从根节点到当前节点的路径。

class Solution {List<List<Integer>> ret = new LinkedList<List<Integer>>();Map<TreeNode, TreeNode> map = new HashMap<TreeNode, TreeNode>();public List<List<Integer>> pathSum(TreeNode root, int targetSum) {if (root == null) {return ret;}Queue<TreeNode> queueNode = new LinkedList<TreeNode>();Queue<Integer> queueSum = new LinkedList<Integer>();queueNode.offer(root);queueSum.offer(0);while (!queueNode.isEmpty()) {TreeNode node = queueNode.poll();int rec = queueSum.poll() + node.val;if (node.left == null && node.right == null) {if (rec == targetSum) {getPath(node);}} else {if (node.left != null) {map.put(node.left, node);queueNode.offer(node.left);queueSum.offer(rec);}if (node.right != null) {map.put(node.right, node);queueNode.offer(node.right);queueSum.offer(rec);}}}return ret;}public void getPath(TreeNode node) {List<Integer> temp = new LinkedList<Integer>();while (node != null) {temp.add(node.val);node = map.get(node);}Collections.reverse(temp);ret.add(new LinkedList<Integer>(temp));}
}