智能家居不断孵化独角兽，获得IoT圈年度最大融资

李彦宏说，移动互联网的时代结束了。

周鸿祎说，互联网下半场就要开启。

那么互联网下一个超级风口，在物联网吗？

所谓物联网，其实就是借助互联网的力量，实现万物互联。实际上物联网已不知不觉融入我们的生活中，给我们带来便捷，比如，智能门锁、ETC 电子自动收费系统等，一开始感觉还挺很新奇的，现在也习以为常了。

甚至可以说，物联网是互联网发展的必然趋势，尤其现在 5G 提供了必要的支持。而且国内很多大公司都已开始布局物联网了。比如众所周知的小米智能家居；还有云计算企业和互联网巨头：阿里云、腾讯云等，都已经纷纷投入大量的人力、资金布局物联网行业。

商机来了，自然对人才的需求也就多了，尤其近几年已经有不少大厂在招聘 Iot 的人才，对这个领域感兴趣的技术人可要把握住机会。

如何学会、学懂物联网？

很多人觉得，物联网很难掌握，这是因为物联网涉及的知识非常庞杂，包括通信技术、嵌入式开发、互联网系统、大数据、人工智能等等，可以说是“盘根错节”。

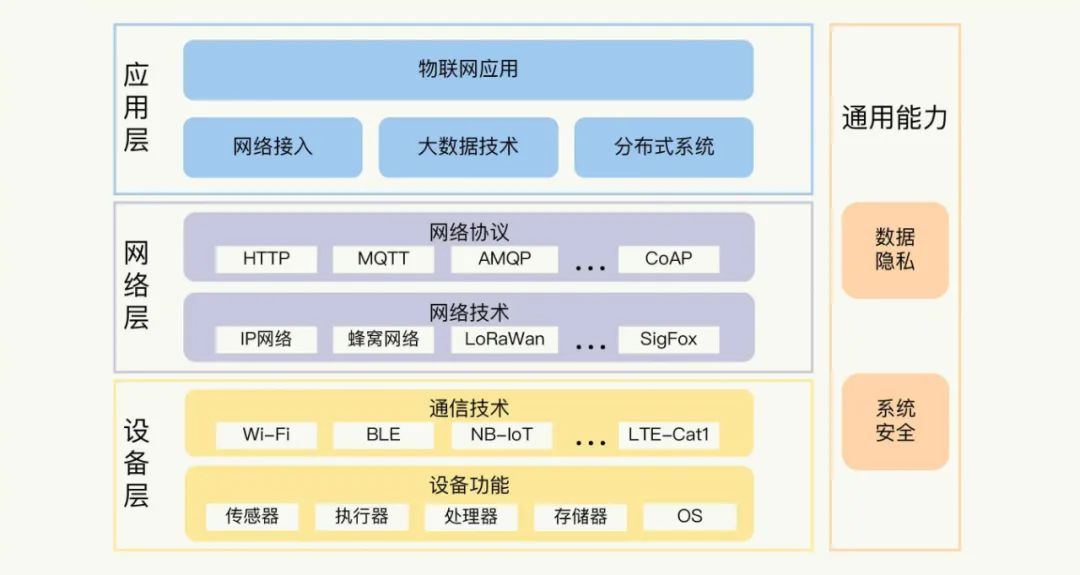
但我看到过一个很不错的方法，把物联网从整个体系结构上，划分成了三个层面：

第一是设备层，也就是各种硬件设备。设备组件有传感器，比如测量温度、湿度、光照强度等参数的设备；也有执行器，比如控制电路通断的继电器、实现物体移动的马达等。

物联网设备，不仅涉及传统嵌入式系统的开发，而且也需要考虑通信技术，比如 Wi-Fi、蓝牙和蜂窝网络等。你只有熟悉它们的特点，才能在实践中做出正确的选择。

第二是网络层，主要关注的是设备与物联网平台的通信协议。

物联网的网络通信仍然是基于互联网的，所以底层还是 TCP/IP 协议。应用中你更多需要了解、掌握的是具体的网络协议，比如 HTTP、MQTT 和 AMQP 等。在做物联网系统设计的时候，你得搞清楚这些协议的适用场景。

第三是应用层，也就是实现具体业务逻辑的地方。

除了像普通互联网后台一样，要面对服务器框架、数据库系统、消息队列等问题外，物联网系统首先需要处理的就是海量的数据。

总结成图的话，就是下面👇这张。

这些内容出自郭朝斌的专栏《物联网开发实战》，对这块我也是挺有兴趣，所以一上线我就入手且加入了课程交流群，可以说这么庞杂的物联网的知识，我还是第一次看到有人能把这些体系梳理清楚、讲出来。如今课程内容已成为物联网岗位面试题。

一句话概括课程内容的话，就是郭朝斌结合了自己在小米生态的工作经验，梳理出物联网领域庞杂的专业知识、剖析物联网关键技术，带大家从 0 基础开始实现一个智能家居项目。

新人首单仅￥59

原价￥129，输入口令「happy2021」立省￥40

作者郭朝斌是谁？

前小米生态链企业秒秒测 IoT 事业部总监，曾先后在诺基亚、微软担任高级工程师。

他有十多年的软硬件领域从业经历，主持设计过用于医药、生鲜行业的冷链监控系统，积累了丰富的物联网理论和实践经验；对于目前全球最大的消费物联网平台之一 -- 小米物联网平台，有丰富的实践经验。可以说郭朝斌对物联网的整个知识体系非常清楚，并对相关技术有深入研究。

这个专栏是如何设计的？

结合简易智能家居项目，深度剖析物联网三大层面的核心知识点。

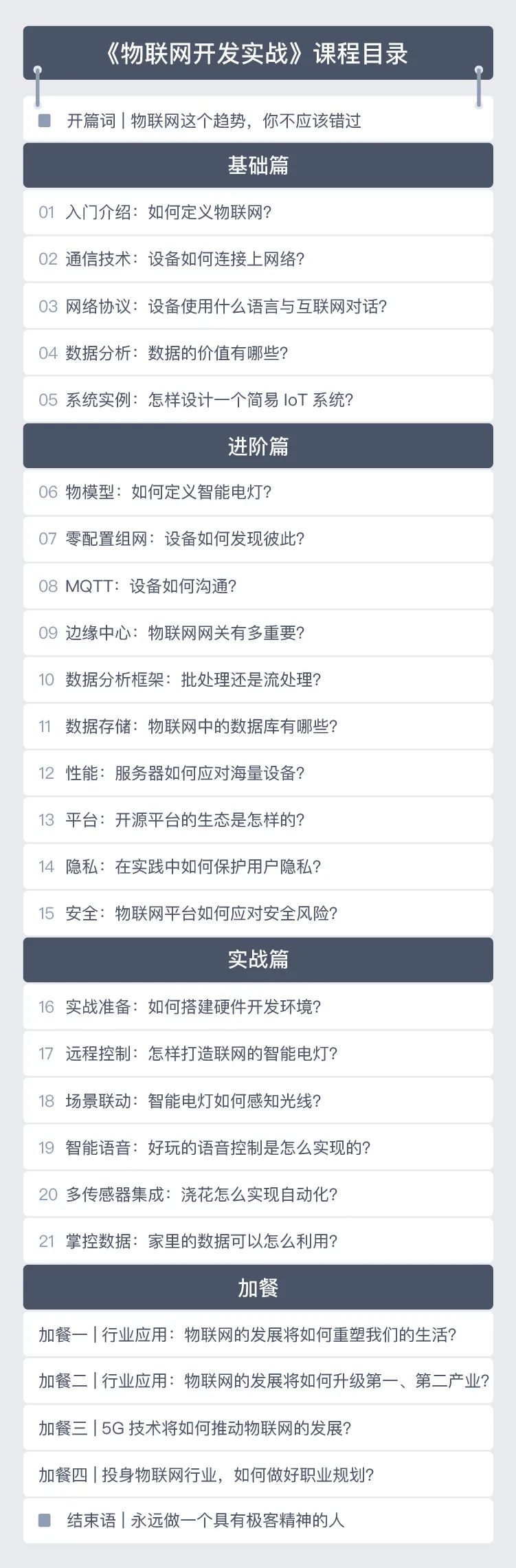
基础篇：首先按照设备接入网络、与平台对话、传输数据和利用数据产生价值的路径，为你介绍物联网系统的基本框架，让你初步理解设备层、网络层和应用层这三大层面；然后通过智能家居场景的简易物联网系统，帮你建立更直观的认知。

某同学的学习笔记，可在课程加餐中获取原图

进阶篇：结合简易智能家居项目，剖析物联网三大层面的核心知识点，并对开源生态、用户隐私、系统安全的实践注意事项做针对性的补充；

实战篇：为你量身定制一个实战项目，围绕智能家居的简易物联网系统，一步一步地讲解实现步骤和注意事项。

其他同学跟着课程完成的作品

加餐：介绍物联网的未来发展趋势和重点实践领域，比如 5G 等新型通信技术的应用。

说了这么多，我们来通过目录来看看详细内容吧：

今天订阅有什么福利？

1、原价￥129，限时拼团 + 口令 [happy2021] 到手仅 ¥89 。

2、新人首单，仅需￥59，今日订阅还可加入[物联网交流群]。

👇 点击「阅读原文」，一顿饭钱，直达软件工程师的乐高游戏！