蓝桥杯 Python 组省赛夺奖班-6 二分法

一、分巧克力

题目

思路

首先确定一下巧克力边长d的上界，这里可以想像把所有巧克力全部融化，平均每个人能分到 sum/k 面积的巧克力(高度不考虑)，那么d的上界为int(math.sqrt(sum/k)).

• 暴力：直接从d的上界开始到1判断是否可行
• 二分：left = 1,right = int(math.sqrt(sum/k)),进行二分

代码

import math
n,k = map(int,input().split())
h = [0]*n
w = [0]*n
for i in range(n):h[i],w[i] = map(int,input().split())
def check(d):num = 0for i in range(n):num += (h[i]//d)*(w[i]//d)if num >= k:return Truereturn False
temp = 0
for i in range(n):temp += h[i]*w[i]
left = 1
right = int(math.sqrt(temp/k))
while(left < right):mid = (left+right+1)//2if check(mid):left = midelse:right = mid-1
print(left)

二、跳石头

题目

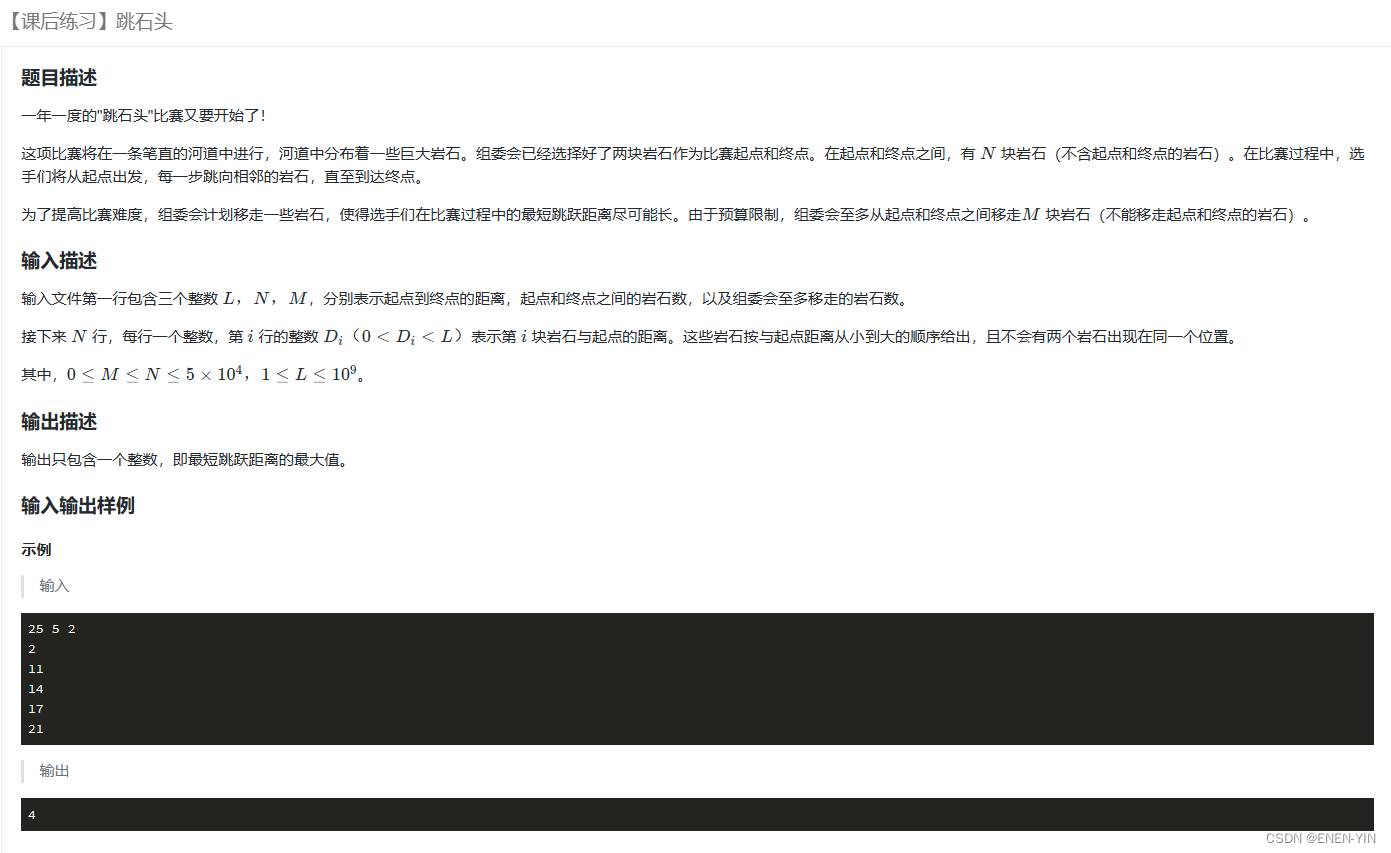
思路

• 暴力：有c(n,m)*n的复杂度明显不可取
• 二分：对于最大的最小间隔，肯定随着最小间隔的增大需要搬走的石头数量变多，假设正确答案为ans，那么对于ans>=d的d搬走m块石头肯定能满足，而对于ans<d的d搬走m块石头必然不能满足
  ps:如果你也是看罗勇军老师的课程，那么注意给的代码有一点小瑕疵：n块石头会分割出n+1段路，最后一段路也要考虑否则会有bug！(虽然能过oj)
  正确的方法：把最后一段路考虑进来，只不过最后一段路的解释不同，不是搬走终点而是搬走终点前一个岩石
  bug样例：

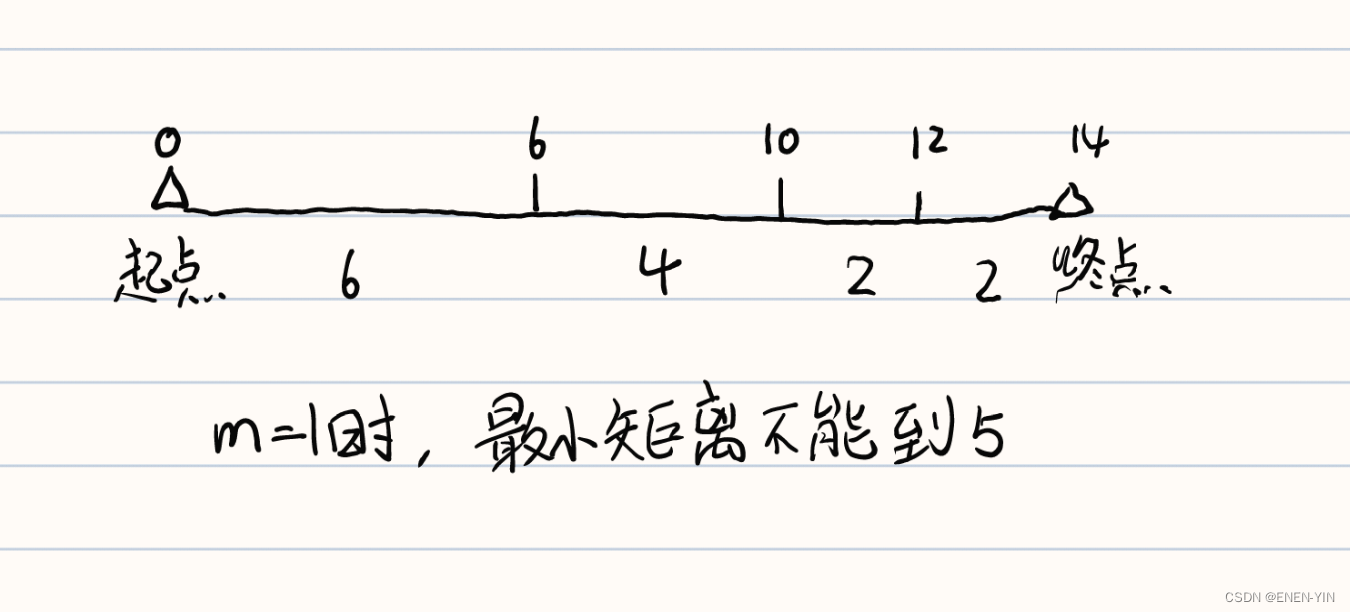
代码

已考虑最后一段：

length,n,m = map(int,input().split())
d = []
for i in range(n):d.append(int(input()))
d.append(length)
def check(gap):num = 0temp = 0for i in range(n+1):if d[i]-temp >= gap:temp = d[i]else:num += 1if num > m:return Falsereturn True
left = 1
right = length
while left < right:mid = (left+right+1)//2if check(mid):left = midelse:right = mid-1
print(left)

三、一元三次方程求解

题目

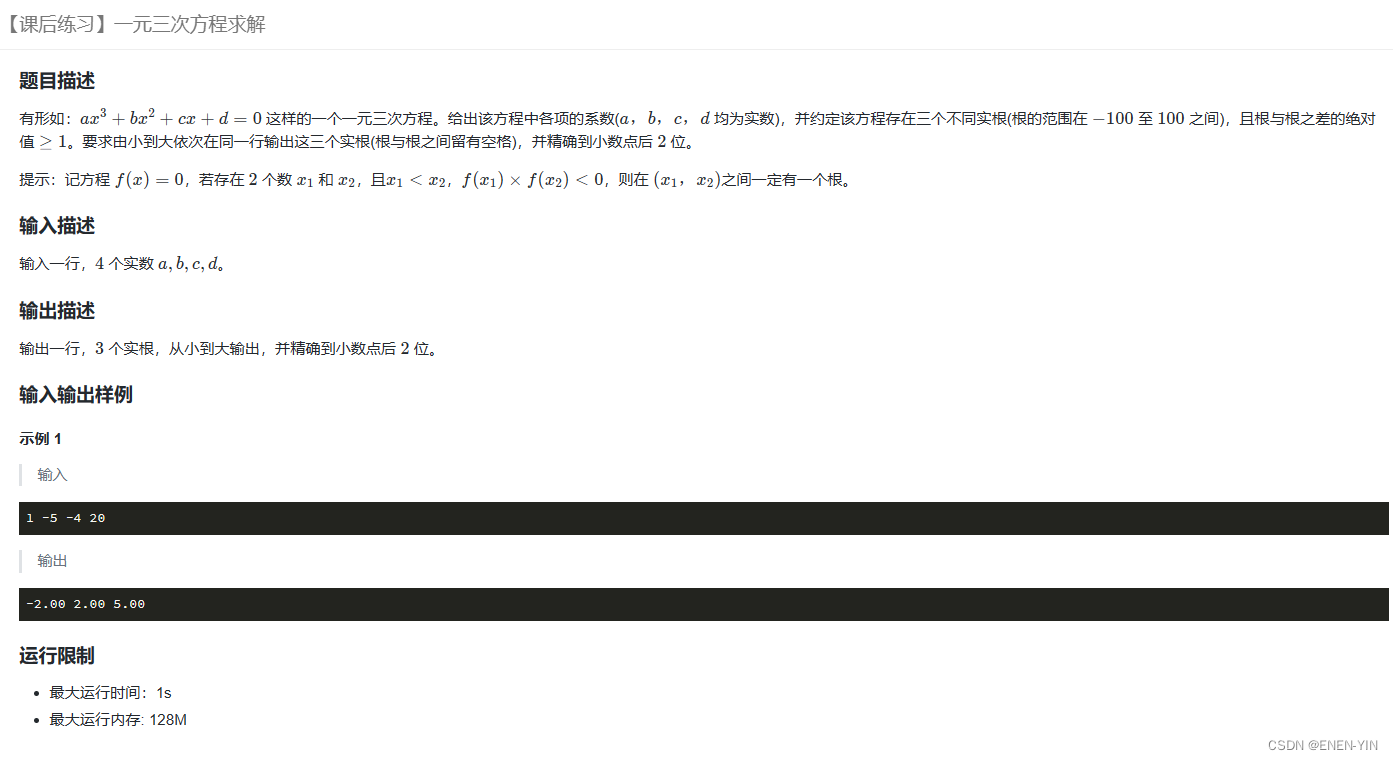
思路

已知根于根的间隔大于等于1，也就是说在任意一个长度为1的区间内(左闭右开)最多只存在一个解，那么如果某个长度为1的区间存在解，那么必然存在两端的值符号相反，就像一根针从一块布穿过，必然两端有一端在布上面，一段在布下面。那么可以使用二分进行查找解。需要注意的是这里精确到小数点后两位，也就是说精度要达到0.001，还有系数是浮点数，不是整数！！！

代码

def myfunc(a,b,c,d,x):return a*(x**3)+b*(x**2)+c*x+d
a,b,c,d = map(float,input().split())
for i in range(-100,101):left = iright = i+1if myfunc(a,b,c,d,left) == 0:print("%.2f"%left,end = " ")continueif myfunc(a,b,c,d,left)*myfunc(a,b,c,d,right) < 0:while (right-left) >= 0.001:mid = (right+left)/2if myfunc(a,b,c,d,mid)*myfunc(a,b,c,d,left) <= 0:right = midelse:left = midprint("%.2f"%left,end = " ")

四、求阶乘

题目

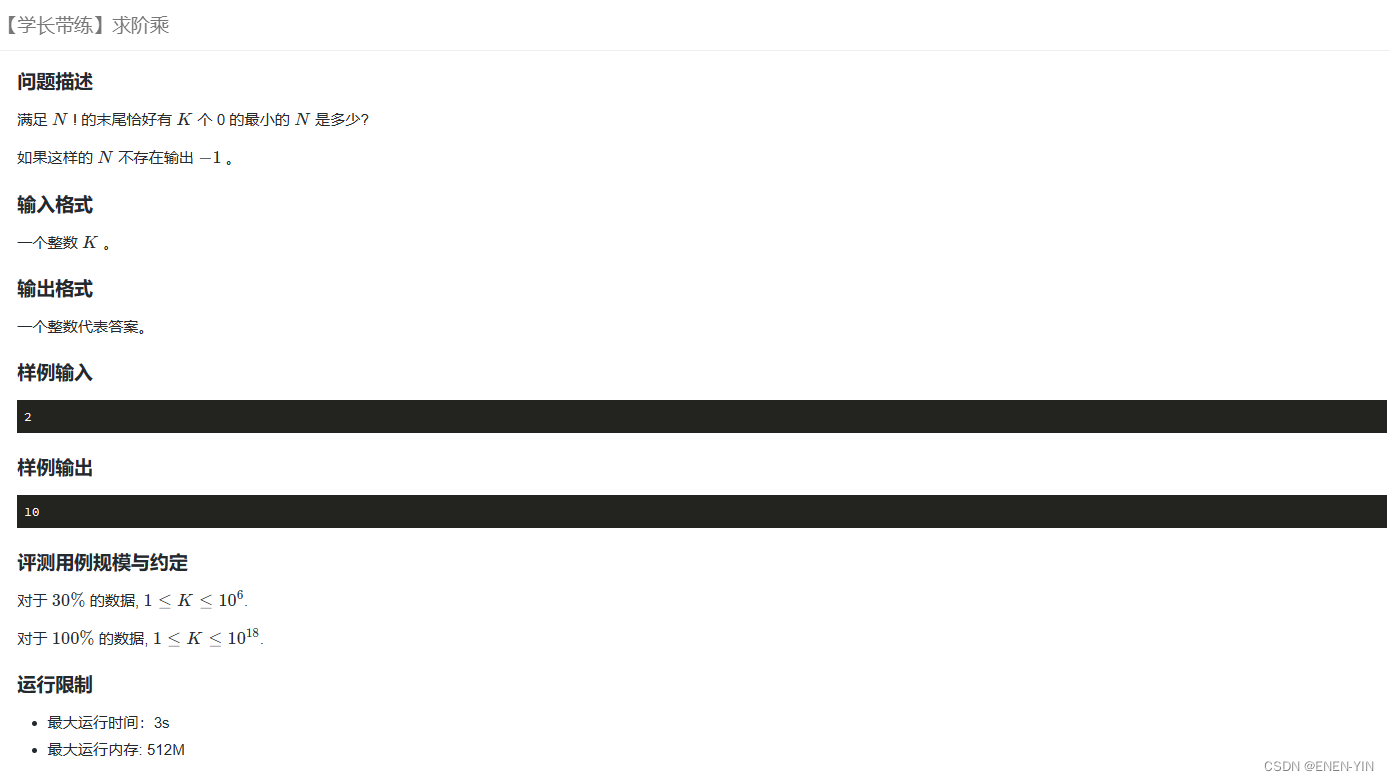
思路

暴力法

直接模拟，会超时

二分+唯一分解

对于阶乘来说，n的阶乘的尾零数肯定不少于n-1的阶乘，也就是说随着n的变大，n阶乘的尾零数单调递增(并不是严格单调递增，可能等于，例如，5和6)，符合二分法的应用场景。
但是实现起来有困难，K最大可为10**18,K的阶乘更是一个天文数字，python无法计算。但是只需要知道有多少个尾零。
这里引入了一个数学知识：
整数惟一分解定理：任何一个大于1的整数n都可以分解成若干个素因数的连乘积，如果不计各个素因数的顺序，那么这种分解是惟一的
那么尾零可以分解成一个一个的10，而10可以分解为2*5，那么只需要知道能分解出多少对2,5就行了，这里观察到前10个数中，2，4，6，8，10都可以分解出2，但是能分解出5的只有5，10，也就是说只需要分析较少的5即可。
如何分解出有多少个5呢？

• 思路1：每隔5就能分解出一个，直接除5 。 例外：25，125，625分别能分解出2，3，4个5
• 思路1改进：每次除5，结果累加，直到为零，也就是把，25，125，625吃干抹尽

代码

暴力法

import math
k = int(input())
n = 5
facn = 24
while True:if len(str(facn*n))-len(str(facn*n).rstrip("0")) == k:print(n)breakif len(str(facn*n))-len(str(facn*n).rstrip("0")) > k:print(-1)breakfacn *= nn += 1

二分+唯一分解

k = int(input())
def getzero(n):cnt = 0while(n > 0):n //= 5cnt += nreturn cnt
left = 5
## 这里的right最少给到10**19，给10**18有一个案例通不过！
## 实际上right给10**100都可以，二分法非常高效！
right = int(10**19)
while(left < right):mid = (left+right)//2if getzero(mid) >= k:right = midelse:left = mid+1
if getzero(left) == k:print(left)
else:print(-1)

五、最少刷题数

题目

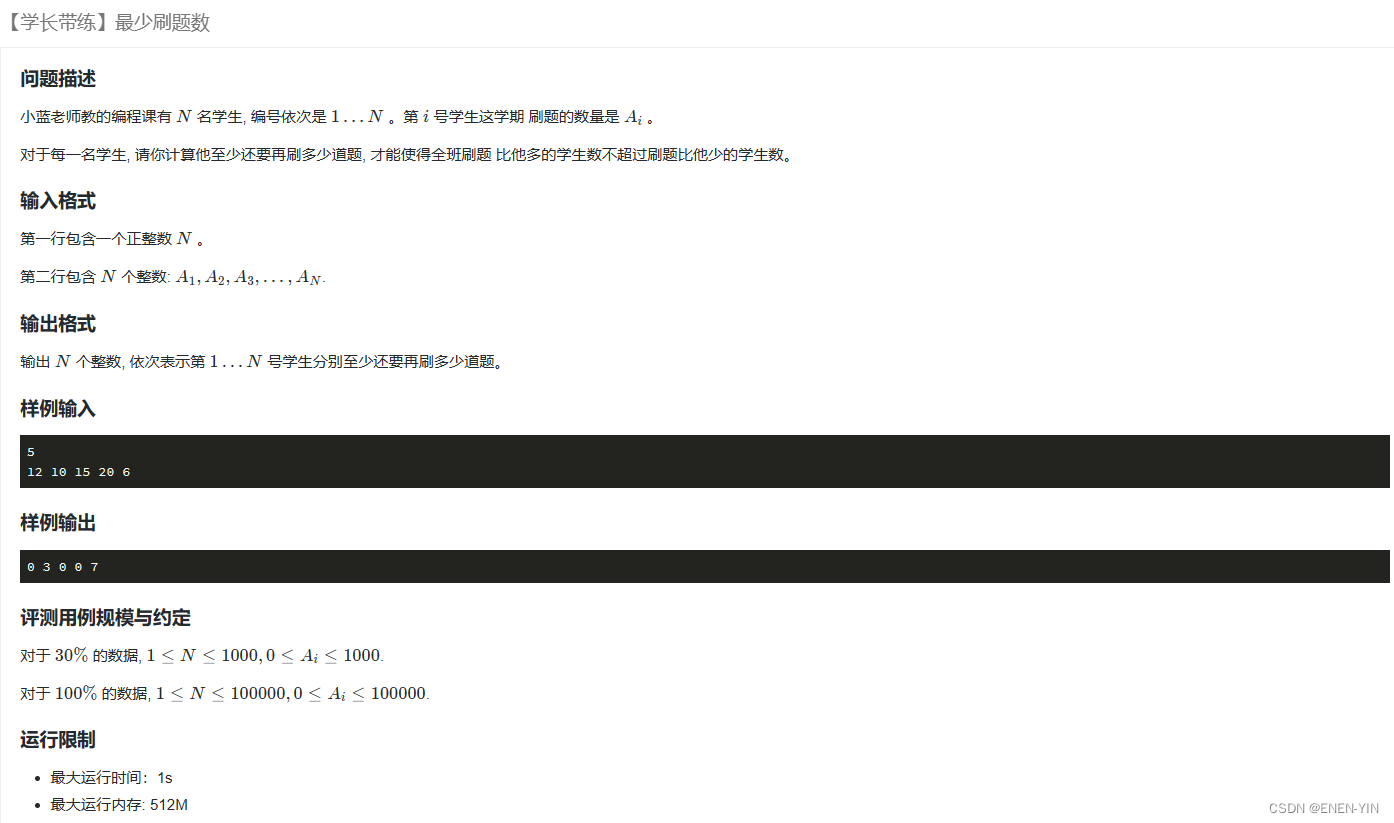
思路

暴力

思路有点难理清，要考虑到重分的人数，比较复杂

前缀和

统计每个分段的人数，然后求出不需要刷题的最少刷题数，以及需要刷题的人最少刷到的题数(有点小拗口，结合代码注释更容易理解)

代码

n = int(input())
a = list(map(int,input().split()))
maxn = max(a)
b = [0]*(maxn+1)
for i in range(n):b[a[i]] += 1
for i in range(1,maxn+1):b[i] += b[i-1]## yes为不用刷题的最小题数
## no 为需要刷题的人 要刷到的最小题数，例如：12 10 15 20 6 中的10、6都至少要刷到13
yes = -1
no = -1
for i in range(1,maxn+1):## b[i-1] 可以看作刷题数为i的人比他刷题少的人数## n-b[i-1] 可以看作刷题数为i的人比他刷题多的人数if b[i-1] >= n-b[i]:if yes == -1:yes = i## 假设刷题少的人 刷到了i道题才能满足## b[i-1]-1是因为 刷题少的人刷了一些题刷到了i道，那么前面的人数会减一## n-b[i-1] 不变是因为我假设他多刷了一些题后刷了i题，那么b[i-1]少了一个，但是又加了一个到b[i]所以抵消了if b[i-1]-1 >= n-b[i]:if no == -1:no = iif yes != -1 and no != -1:break## yes、no都探测完，提前结束
for i in range(n):if a[i] >= yes:## 大于等于yes不用刷print(0,end = " ")else:## 小于yes刷到noprint(no-a[i],end = " ")

六、最大子矩阵

题目

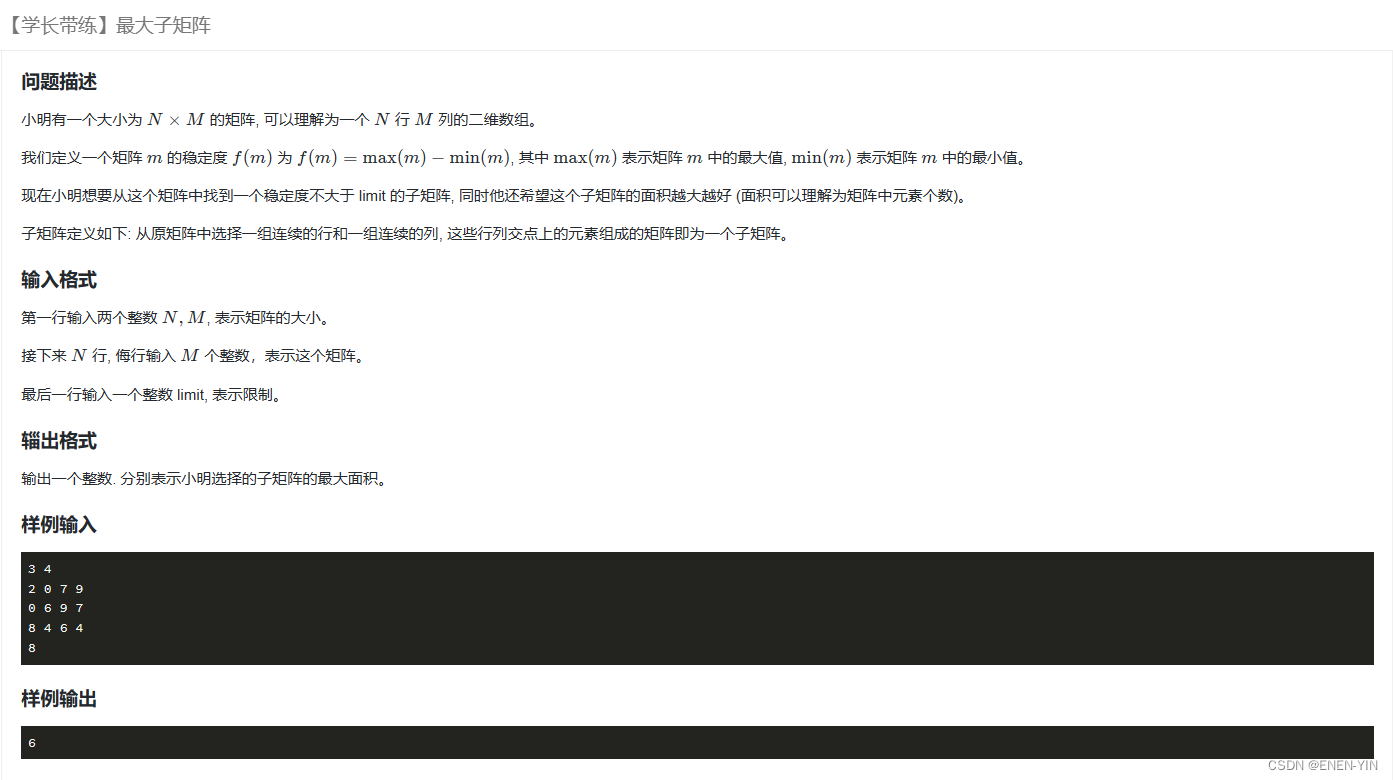
思路

二分面积

很遗憾这里并不能像搬石头或者巧克力一样直接对结果进行二分，因为这里是二维的，前两个都是一维的。
验证：

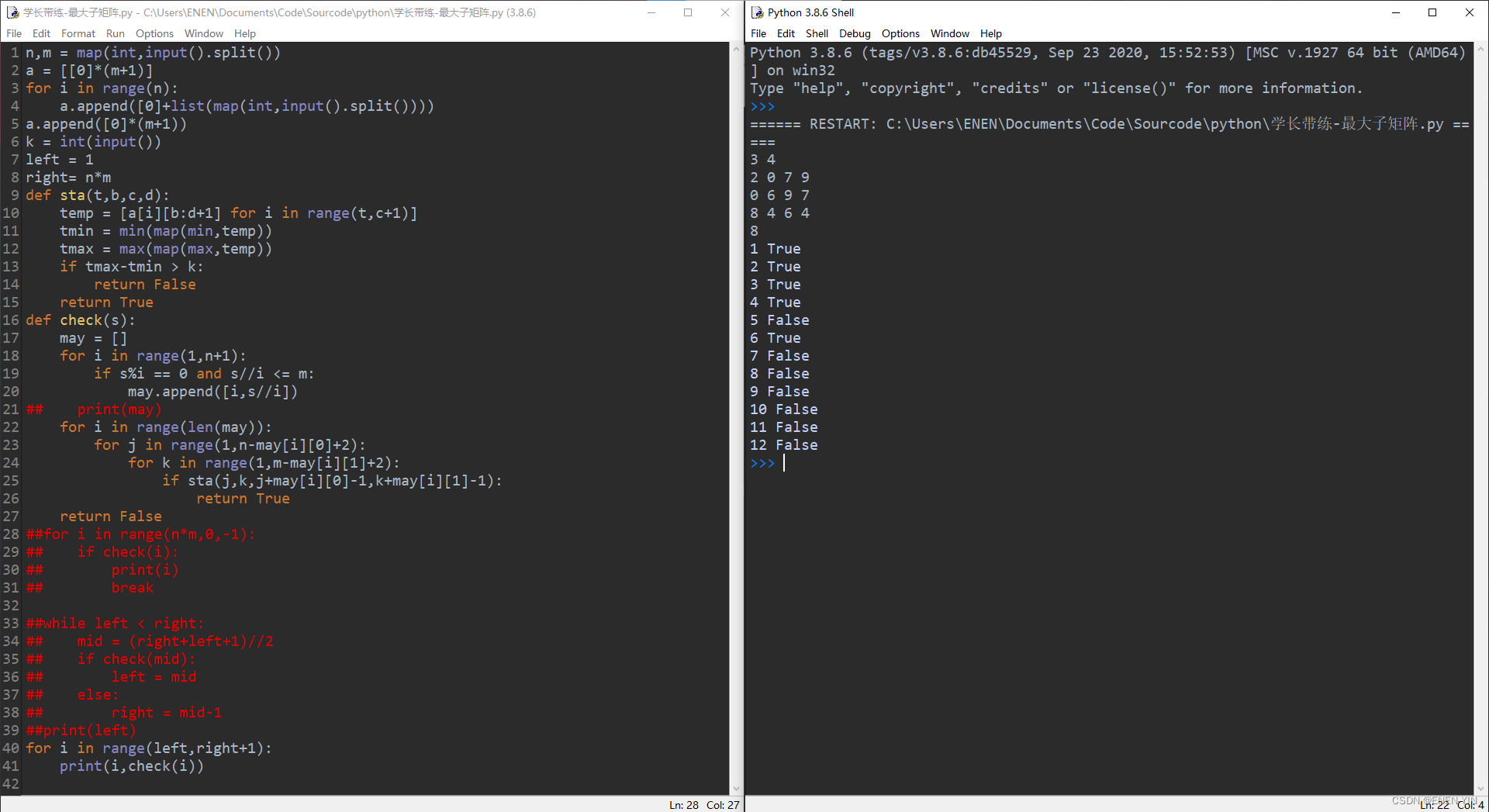
后面进行了改进直接倒序遍历尝试，这样其实思路就是暴力法了。直接超时，没有评测结果

二分m

这里可以计算一下暴力的复杂度为o(nm *nm *nm)
(学长说是o($n^2\ast m^2$) ，但是我怎么感觉是o($n^3\ast m^3$))

• 第一个nm是子矩阵的左上角坐标一共有n*m种
• 第二个nm是子矩阵的长宽一共有n*m中
• 第三个nm是遍历子矩阵中查找最大最小元素
  观察到m的范围不可忍受，n非常小，所以对m进行二分，将一个m变为$lo{g}_2^m$（很显然这里优化的是第二个中的m，第一个和第三个没法优化）

代码

尝试二分s失败后改成的暴力法

n,m = map(int,input().split())
a = [[0]*(m+1)]
for i in range(n):a.append([0]+list(map(int,input().split())))
a.append([0]*(m+1))
k = int(input())
left = 1
right= n*m
def sta(t,b,c,d):temp = [a[i][b:d+1] for i in range(t,c+1)]tmin = min(map(min,temp))tmax = max(map(max,temp))if tmax-tmin > k:return Falsereturn True
def check(s):may = []for i in range(1,n+1):if s%i == 0 and s//i <= m:may.append([i,s//i])
##    print(may)for i in range(len(may)):for j in range(1,n-may[i][0]+2):for k in range(1,m-may[i][1]+2):if sta(j,k,j+may[i][0]-1,k+may[i][1]-1):return Truereturn False
for i in range(n*m,0,-1):if check(i):print(i)break##while left < right:
##    mid = (right+left+1)//2
##    if check(mid):
##        left = mid
##    else:
##        right = mid-1
##print(left)

二分m

• 学长的代码（个人觉得有点不容易懂）

N,M = map(int,input().split())
a = [[0]*(M+1)]
maxs = 0
for i in range(N):a.append([0]+list(map(int,input().split())))
limit = int(input())
def sta(i,j,h,w):submotrix = [a[k][j:j+w] for k in range(i,i+h)]if max(map(max,submotrix))-min(map(min,submotrix)) > limit:return Falsereturn True
def check(n,k):global maxs## 起始行号i ,共n行,k列for i in range(1,N-n+2):for j in range(1,M-k+2):if sta(i,j,n,k):if n*k > maxs:maxs = n*kreturn Truereturn False## 子矩阵大小为i*mid
for i in range(1,N):left = 1right = Mwhile(left < right):mid = (left+right)//2if check(i,mid):left = mid+1else:right = mid
print(maxs)

• 思路相同，自己写的代码(固定n，二分m，每个n都有一个最大的子矩阵，在这n个最大子矩阵中取最大的即为所求)

N,M = map(int,input().split())
a = [[0]*(M+1)]
maxs = 0
for i in range(N):a.append([0]+list(map(int,input().split())))
limit = int(input())
def sta(i,j,h,w):submotrix = [a[k][j:j+w] for k in range(i,i+h)]if max(map(max,submotrix))-min(map(min,submotrix)) > limit:return Falsereturn True
def check(n,k):global maxs## 起始行号i列号j ,共n行,k列for i in range(1,N-n+2):for j in range(1,M-k+2):if sta(i,j,n,k):return True
##                if n*k > maxs:
##                    maxs = n*k
##                    return Truereturn False
ans = []
## 子矩阵大小为i*mid
for i in range(1,N):left = 1right = Mmaxs = 0while(left < right):mid = (left+right+1)//2if check(i,mid):left = midelse:right = mid-1ans.append(i*left)
print(max(ans))

这道题目上面两种写法都不能过oj，因为这是给java设计的题目，python规定时间内完不成。