本文主要是介绍古典密码与哈希函数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
古典密码与哈希函数
凯撒密码
加密公式：密文 = (明文 + 位移数) Mod 26
解密公式：明文 = (密文 - 位移数) Mod 26
例：helloworld通过凯撒密码加密，加密秘钥为3，加密后密文为khoorzruog
部分凯撒密码代码
do{//先判断再转charif(a[i]+k>122)//如果右移后ascii码值超过122 b[i]=(char)(a[i]+k-26);//通过减26实现字母表的循环 elseb[i]=(char)(a[i]+k); //字符右移k位(依照ascii码顺序) i++; }while(a[i]!='\0'); //当遇到字符串结束符号时循环结束 do{if(a[i]-k<97)//如果左移后ascii码值小于97 b[i]=(char)(a[i]-k+26);//通过减26实现字母表的循环 elseb[i]=(char)(a[i]-k); //字符右移k位(依照ascii码顺序) i++; }while(a[i]!='\0');栅栏密码
所谓栅栏密码，就是把要加密的明文分成N个一组，然后把每组的第1个字连起来，形成一段无规律的话。 不过栅栏密码本身有一个潜规则，就是组成栅栏的字母一般不会太多。（一般不超过30个，也就是一、两句话）
例如明文：I LIKE DOG AND CAT
加密过程：I I E O A D A
L K D G N C T (两栏)
解密就是按照上下上下的顺序连成一句话并在合适的位置加上空格：I LIKE DOG AND CAT
可以根据明文字符数来考虑加密时所分成的栏数。
栅栏密码部分代码：
加密
do{ if(i%2==0){b[j]=a[i];//偶数下标的字母给到数组b j++;} else{c[k]=a[i];//奇数下标的字母给到数组c k++;}i++; }while(a[i]!='\0'); //当遇到字符串结束符号时循环结束i=0;while(c[i]!='\0'){b[j]=c[i];//将c中的字母合并到b i++;j++;} printf("密文为：\n"); puts(b);//输出密文数组b解密
if(len%2==0) k=len/2;else k=len/2+1; k=12/2=6 0-5放偶数下标字符，6-11放奇数下标字符 k=9/2=4 0-3放偶数下标字符4个，4-8放奇数下标字符5个 for(i=0;i<len;i++){if(i%2==0){//根据栅栏密码的规则将字母位置还原 b[i]=a[j];j++;}else{b[i]=a[k];k++;}}培根密码
培根密码，又名倍康尼密码（英语：Bacon's cipher）是由法兰西斯·培根发明的一种隐写术。
加密时，明文中的每个字母都会转换成一组五个英文字母。其转换依靠下表：
加密者需使用两种不同字体，分别代表A和B。准备好一篇包含相同AB字数的假信息后，按照密文格式化假信息，即依密文中每个字母是A还是B分别套用两种字体。
解密时，将上述方法倒转。所有字体一转回A，字体二转回B，以后再按上表拼回字母。
法兰西斯·培根另外准备了一种方法，其将大小写分别看作A与B，可用于无法使用不同字体的场合（例如只能处理纯文本时）。但这样比起字体不同更容易被看出来，而且和语言对大小写的要求也不太兼容。
培根密码本质上是将二进制信息通过样式的区别，加在了正常书写之上。培根密码所包含的信息可以和用于承载其的文章完全无关。
当铺密码
它通过一个汉字中隐藏的信息：笔画数，来将汉字和数字关联起来，将汉字定义为明文，将数字定义为密文，加密是将数字映射到对应笔画的汉字，解密是将汉字按照笔画映射回数字。或者当前汉字有多少笔画出头，就是转化成数字几。
例如密文：大 中 口 由 人 甲 工
通过数汉字出头数解密为：5201314
摩斯电码
摩斯电码(摩尔斯电码)是一种发报用的信号代码，是一种替代密码，用点(Dot)和划(Dash)的组合来表示各个英文字母或标点。
例如密文：.. ._.. ___ ..._ . _.__ ___ .._
解密：I LOVE YOU
DES算法
DES算法为密码体制中的对称密码体制，又被称为美国数据加密标准，是1972年美国IBM公司研制的对称密码体制加密算法。 明文按64位进行分组，密钥长64位，密钥事实上是56位参与DES运算（第8、16、24、32、40、48、56、64位是校验位， 使得每个密钥都有奇数个1）分组后的明文组和56位的密钥按位替代或交换的方法形成密文组的加密方法。
对称性:DES是对称的，也就是说它使用同一个密钥来加密和解密数据。
分组性:DES还是一种分组加密算法，该算法每次处理固定长度的数据段，称之为分组。DES分组的大小是64位，如果加密的数据长度不是64位的倍数，可以按照某种具体的规则来填充位。
“混乱和扩散”的原则:混乱的目的是为隐藏任何明文同密文、或者密钥之间的关系，而扩散的目的是使明文中的有效位和密钥一起组成尽可能多的密文。两者结合到一起就使得安全性变得相对较高。
DES算法入口参数：
key：7个字节共56位的工作密钥
data：8个字节共64位的需要被加密或被解密的数据
mode：DES工作方式，加密或者解密
主要流程
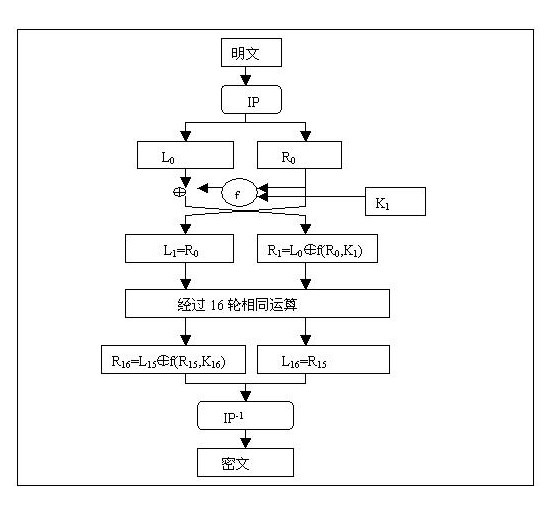des算法流程图
DES算法把64位的明文输入块变为64位的密文输出块，它所使用的密钥也是64位，整个算法的主流程图如下：
置换规则表
其功能是把输入的64位数据块按位重新组合，并把输出分为L0、R0两部分，每部分各长32位，其置换规则见下表：
58,50,42,34,26,18,10,2,60,52,44,36,28,20,12,4,
62,54,46,38,30,22,14,6,64,56,48,40,32,24,16,8,
57,49,41,33,25,17,9,1,59,51,43,35,27,19,11,3,
61,53,45,37,29,21,13,5,63,55,47,39,31,23,15,7,
即将输入的第58位换到第一位，第50位换到第2位，...，依此类推，最后一位是原来的第7位。L0、R0则是换位输出后的两部分，L0是输出的左32位，R0 是右32位，例：设置换前的输入值为D1D2D3......D64，则经过初始置换后的结果为：L0=D58D50...D8；R0=D57D49...D7。
经过16次迭代运算后。得到L16、R16，将此作为输入，进行逆置换，即得到密文输出。逆置换正好是初始置换的逆运算。例如，第1位经过初始置换后，处于第40位，而通过逆置换，又将第40位换回到第1位，其逆置换规则如下表所示：
40,8,48,16,56,24,64,32,39,7,47,15,55,23,63,31,
38,6,46,14,54,22,62,30,37,5,45,13,53,21,61,29,
36,4,44,12,52,20,60,28,35,3,43,11,51,19,59,27,
34,2,42,10,50,18,58 26,33,1,41,9,49,17,57,25,
放大换位表
32,1,2,3,4,5,4,5,6,7,8,9,8,9,10,11,
12,13,12,13,14,15,16,17,16,17,18,19,20,21,20,21,
22,23,24,25,24,25,26,27,28,29,28,29,30,31,32,1,
单纯换位表
16,7,20,21,29,12,28,17,1,15,23,26,5,18,31,10,
2,8,24,14,32,27,3,9,19,13,30,6,22,11,4,25,
功能表
在f(Ri,Ki）算法描述图中，S1,S2...S8为选择函数，其功能是把48bit数据变为32bit数据。下面给出选择函数Si(i=1,2......8）的功能表：
选择函数Si
S1:
14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7,
0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8,
4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0,
15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13,
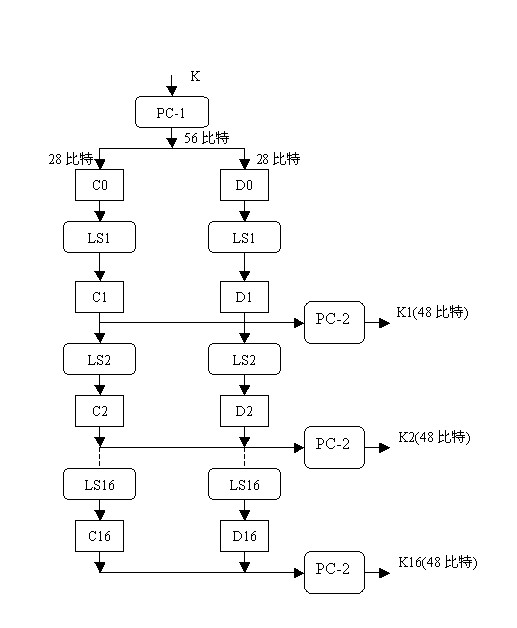des算法
S2:
15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10,
3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5,
0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15,
13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9,
S3:
10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8,
13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1,
13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7,
1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12,
S4:
7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15,
13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9,
10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4,
3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14,
S5:
2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9,
14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6,
4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14,
11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3,
S6:
12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11,
10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8,
9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6,
4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13,
S7:
4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1,
13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6,
1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2,
6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12,
S8:
13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7,
1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2,
7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8,
2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11,
在此以S1为例说明其功能，我们可以看到：在S1中，共有4行数据，命名为0，1、2、3行；每行有16列，命名为0、1、2、3，......，14、15列。
现设输入为：D=D1D2D3D4D5D6
令：列=D2D3D4D5
行=D1D6
然后在S1表中查得对应的数，以4位二进制表示，此即为选择函数S1的输出。下面给出子密钥Ki（48bit）的生成算法
子密钥的算法
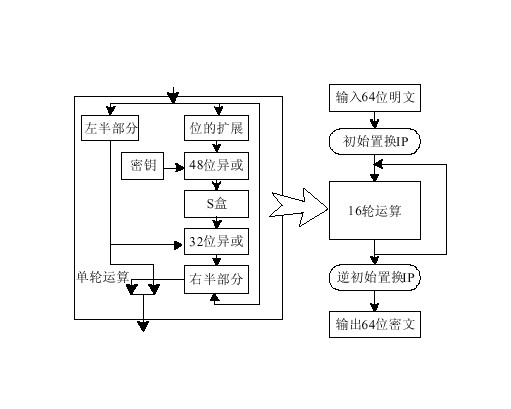des算法
从子密钥Ki的生成算法描述图中我们可以看到：初始Key值为64位，但DES算法规定，其中第8、16、......64位是奇偶校验位，不参与DES运算。故Key 实际可用位数便只有56位。即：经过缩小选择换位表1的变换后，Key 的位数由64 位变成了56位，此56位分为C0、D0两部分，各28位，然后分别进行第1次循环左移，得到C1、D1，将C1（28位）、D1（28位）合并得到56位，再经过缩小选择换位2，从而便得到了密钥K0（48位）。依此类推，便可得到K1、K2、......、K15，不过需要注意的是，16次循环左移对应的左移位数要依据下述规则进行：
循环左移位数
1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1
以上介绍了DES算法的加密过程。DES算法的解密过程是一样的，区别仅仅在于第一次迭代时用子密钥K15，第二次K14、......，最后一次用K0，算法本身并没有任何变化。
MD5算法
MD5算法的原理可简要的叙述为：MD5码以512位分组来处理输入的信息，且每一分组又被划分为16个32位子分组，经过了一系列的处理后，算法的输出由四个32位分组组成，将这四个32位分组级联后将生成一个128位散列值。
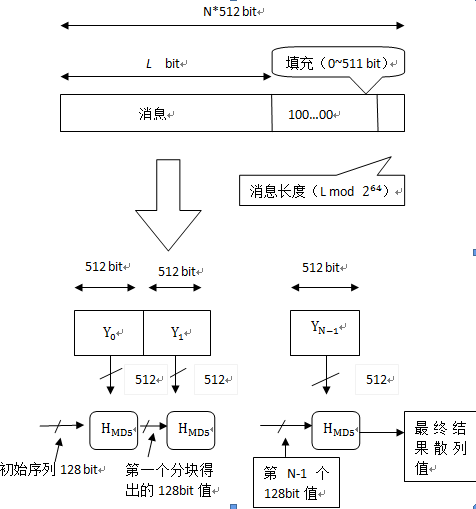
MD5算法的整体流程图
按位补充数据
在MD5算法中，首先需要对信息进行填充，这个数据按位(bit)补充，要求最终的位数对512求模的结果为448。也就是说数据补位后，其位数长度只差64位(bit)就是512的整数倍。即便是这个数据的位数对512求模的结果正好是448也必须进行补位。补位的实现过程：首先在数据后补一个1 bit； 接着在后面补上一堆0 bit, 直到整个数据的位数对512求模的结果正好为448。总之，至少补1位，而最多可能补512位 [8] 。
扩展长度
在完成补位工作后，又将一个表示数据原始长度的64 bit数(这是对原始数据没有补位前长度的描述，用二进制来表示)补在最后。当完成补位及补充数据的描述后，得到的结果数据长度正好是512的整数倍。也就是说长度正好是16个(32bit) 字的整数倍 [8] 。
初始化MD缓存器
MD5运算要用到一个128位的MD5缓存器，用来保存中间变量和最终结果。该缓存器又可看成是4个32位的寄存器A、B、C、D，初始化为 [8] :
A ： 01 23 45 67
B： 89 ab cd ef
C： fe dc ba 98
D： 76 54 32 10
处理数据段
首先定义4个非线性函数F、G、H、I，对输入的报文运算以512位数据段为单位进行处理。对每个数据段都要进行4轮的逻辑处理，在4轮中分别使用4个不同的函数F、G、H、I。每一轮以ABCD和当前的512位的块为输入，处理后送入ABCD(128位) [8] 。
输出
信息摘要最终处理成以A, B, C, D 的形式输出。也就是开始于A的低位在前的顺序字节，结束于D的高位在前的顺序字节 [8] 。
这篇关于古典密码与哈希函数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
