ECCV 2022 | STDANet：基于可变形注意力的视频去模糊

原文链接：https://www.techbeat.net/article-info?id=3932
作者：张慧琮

视频去模糊的关键在于利用连续视频帧的清晰像素恢复中间帧的模糊像素。因此，主流方法通过融合多帧像素恢复模糊的中间帧。然而，这些方法没有考虑视频帧中像素的模糊程度，其实不是所有的像素都是对恢复有利的，引入视频段中模糊的像素将导致其去模糊效果不够理想。
为了解决这个问题，我们提出了STDANet，我们通过考虑视频帧中像素的模糊程度，提取视频段中清晰的像素信息，从而获得更好的去模糊结果。

论文链接：
https://arxiv.org/abs/2207.10852
代码链接：
https://github.com/huicongzhang/STDAN
项目主页：
https://vilab.hit.edu.cn/projects/stdan

一、引言

视频去模糊方法的关键在于使用多帧的像素信息恢复中间模糊帧。早期的视频去模糊方法[1-2]直接使用CNN网络融合多帧像素信息，因为其非对齐的相邻帧，他们并没有充分利用相邻帧的像素信息。近期的视频去模糊方法[3-4]使用光流对相邻帧进行对齐，然后使用CNN网络对对齐的视频帧进行融合并恢复中间帧。然而，他们忽略了视频帧之间的像素模糊程度的差异，不是所有的像素都是对重建有利的，引入模糊像素将导致去模糊效果下降。

为了解决这个问题，我们提出了STDANet，通过考虑视频帧中像素的模糊程度，提取视频段中清晰的像素信息，从而更好地恢复模糊的中间帧。 另外为了对相邻帧进行运动补偿，我们设计了一个轻量化的运动估计分支用于估计粗糙的光流。

二、解决方案

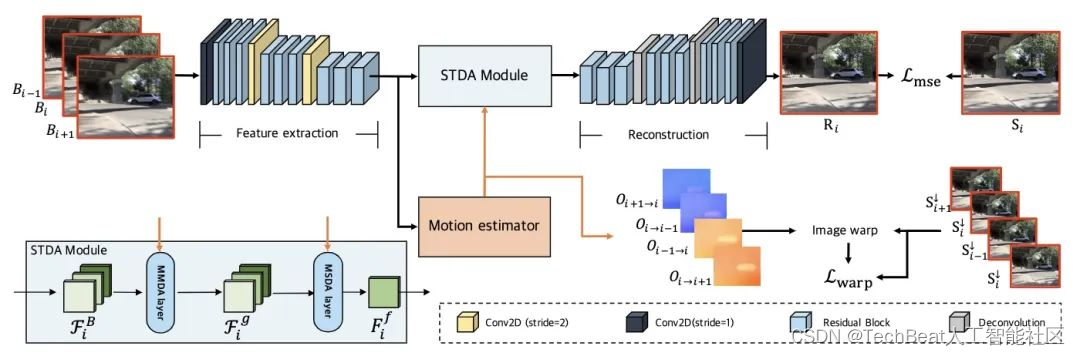
图1 STDANet的总体框架图

所提出的STDANet的总体框架如图1所示。 给定三帧连续视频帧 B i = { B k } k = i − 1 i + 1 \mathcal{B}_i = \left\{\mathbf{B}_k \right\}_{k=i-1}^{i+1} Bi​={Bk​}k=i−1i+1​ 作为输入，所提出的STDANet的目的是恢复中间帧 ${\mathbf{R}}_i$ 。首先连续视频帧输入到特征提取器，得到连续视频帧的特征。然后运动估计分支根据所提取特征，估计连续帧之间的粗糙光流。接着我们所提出的STDA模块通过估计得到的粗糙光流的引导，提取多帧特征的清晰像素信息，得到重建特征 ${\mathbf{F}}_i^f$ ，最后重建网络将 ${\mathbf{F}}_i^f$ 恢复到RGB图像空间，完成重建。

运动估计分支

此前的视频去模糊方法大多使用光流对齐相邻帧与中间帧，这需要较为大型的光流估计网络如PWC-Net[5]以估计准确的光流。而在我们的STDANet中光流不直接用于相邻帧与中间帧之间的对齐，而是用于引导STDA模块采样视频段中的清晰像素，这种光流引导的思路对于不准确的光流更加鲁棒，因此我们可以用更加轻量化的运动估计分支来估计粗糙光流，从而减少计算量，此外由于没有去模糊数据集的真实光流，我们在重建损失函数 ${\mathcal{L}}_{mse}$ 之外采用对齐损失函数 ${\mathcal{L}}_{warp}$ 给予运动估计分支训练信号，运动估计分支与主网络一起进行训练。 给定连续视频帧 ${\mathcal{F}}_i^b={\left\{{\mathbf{F}}_k^b|{\mathbf{F}}_k^b\in {\mathbb{R}}^{C\times H\times W}\right\}}_{k=i-1}^{i+1}$ 作为输入，运动估计分支估计其前后向的光流 O i = { O k → k + 1 ∣ k = i − 1 , i } ∪ { O k + 1 → k ∣ k = i − 1 , i } \mathcal{O}_i = \left\{\mathbf{O}_{k \rightarrow k + 1} | k = i - 1, i \right\} \cup \left\{\mathbf{O}_{k + 1 \rightarrow k} | k = i - 1, i \right\} Oi​={Ok→k+1​∣k=i−1,i}∪{Ok+1→k​∣k=i−1,i} 其中 ${\mathbf{O}}_{m\to n}$ 代表第m帧到第n帧的光流。

时空可变形注意力模块

为了获取视频帧之间的清晰像素信息，我们提出时空可变形注意力模块。遵循“粗到细”的策略，时空可变形注意力模块包含两层注意力层，分别为多对多注意力层，多对一注意力层。其网络结构如下图：

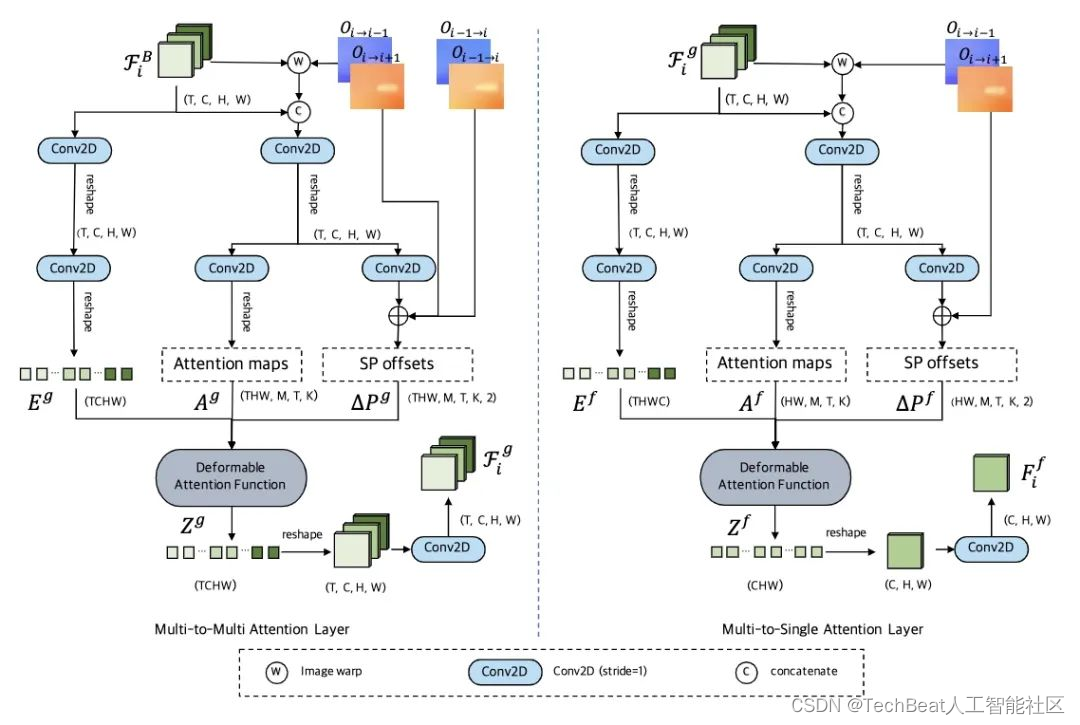
图2 时空可变形注意力模块框架图

如图2左图多对多注意力示意图所示，给定 $T$ 帧输入帧特征 ${\mathcal{F}}_i^b={\left\{{\mathbf{F}}_k^b|{\mathbf{F}}_k^b\in {\mathbb{R}}^{C\times H\times W}\right\}}_{k=i-1}^{i+1}$ ，我们使用光流把相邻帧对齐到中间帧 ${\mathbf{F}}_i^b$ ，得到对齐后的特征 ${\mathcal{F}}_i^w$ ，接着我们把特征 ${\mathcal{F}}_i^w$ 与 ${\mathcal{F}}_i^b$ 拼接在一起送入多层卷积层得到注意力图 ${\mathbf{A}}^g\in {\mathbb{R}}^{Q\times M\times T\times K}$ 以及采样点偏移 $\Delta {\mathbf{P}}^g\in {\mathbb{R}}^{Q\times M\times T\times K\times 2}$ ，其中 $Q=THW$ ，M、T、K分别代表注意力头数量、帧数以及采样点的数量。 ${\mathbf{A}}^g$ 采用 ${\sum }_{t=1}^T{\sum }_{k=1}^K{\mathbf{A}}_{mtqk}^g=1$ 进行归一化。然后 ${\mathcal{F}}_i^b$ 经过两层卷积层后，我们可以得到展开后的特征 ${\mathbf{E}}^g\in {\mathbb{R}}^{THWC}$ 。接着，我们通过可变形注意力操作[6]得到融合特征 ${\mathbf{Z}}^g\in {\mathbb{R}}^{TCHW}$ 。

${\mathbf{Z}}^g=\mathcal{D}\left({\mathbf{A}}^g,\varphi \left(\Delta {\mathbf{P}}^g,{\mathcal{O}}_i\right),{\mathbf{E}}^g\right)$

其中 $\mathcal{D},\varphi ,{\mathcal{O}}_i$ 分别为可变形注意力操作、光流相加操作以及前后向光流。 最后，${\mathbf{Z}}^g$ 重新reshape为4维，再经过一层卷积后得到最后的融合特征 ${\mathcal{F}}_i^g$ 。

如图2右图多对一注意力层示意图，多对一注意力层以初步融合的特征 ${\mathcal{F}}_i^g$ 作为输入，得到中间帧的融合特征 ${\mathbf{F}}_i^f$ 。 与多对多注意力层不同的是，多对一注意力层是把连续视频帧的清晰像素信息融合于一帧而不是多帧。 因此在多对一注意力层中，融合特征 ${\mathbf{Z}}^f\in {\mathbb{R}}^{CHW}$ 可通过如下公式得到

Z f = D ( A f , ϕ ( Δ P f , { O k → i ∣ k = i − 1 , i + 1 } ) , E f ) \mathbf{Z}^{f}=\mathcal{D}\left(\mathbf{A}^{f}, \phi\left(\Delta \mathbf{P}^{f},\left\{\mathbf{O}_{k \rightarrow i} \mid k=i-1, i+1\right\}\right), \mathbf{E}^{f}\right) Zf=D(Af,ϕ(ΔPf,{Ok→i​∣k=i−1,i+1}),Ef)

其中， ${\mathbf{A}}^f\in {\mathbb{R}}^{HW\times M\times T\times K}$ , $\Delta {\mathbf{P}}^f\in {\mathbb{R}}^{HW\times M\times T\times K\times 2}$ 以及 ${\mathbf{E}}^f\in {\mathbb{R}}^{TCHW}$ 分别为注意力图、采样点偏移以及展开的特征。 同样 ${\mathbf{Z}}^f\in {\mathbb{R}}^{CHW}$ reshape 到3维后经过一层卷积，得到最后的融合特征 ${\mathbf{F}}_i^f$ 。

经过从多对多到多对一注意力层的提取，我们得到包含多帧清晰像素信息的特征 ${\mathbf{F}}_i^f$ 。 我们可视化了多对一注意力层的注意力图，更好得展示其提取清晰像素的能力。

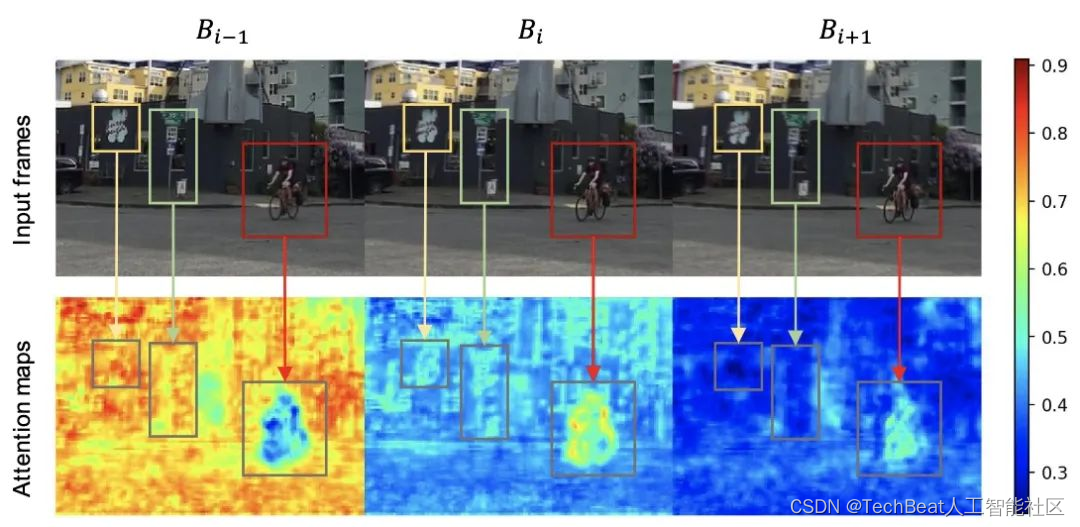
图3 多对一注意力层注意力图可视化

从图3中的例子可以看出，越清晰的区域将获得越高的注意力权重。例如在 $B_{i-1}$ 帧中，骑自行车的人（红框标出位置）是模糊的，因此其相关区域注意力权重也比较低。相反在 $B_i$ 红框区域比较清晰，其对应区域的注意力权重也较高。 总而言之，时空可变形注意力模块能通过赋予视频段中清晰区域更高的权重，从而有效地提取视频段中清晰的像素信息。

三、实验结果

我们把STDANet与其他SOTA方法在GoPro、DVD以及BSD三个数据集上进行了比较。其结果如表1-3所示，STDANet超过了以往的SOTA方法。特别地，$Our{s}^{\ast }$ 代表 STDANet-Stack，STDANet-Stack 采用与TSP[3]以及ARVo[4]一样的级联渐进式结构（cascaded progressive structure）。

表1 DVD数据集量化结果

表2 GoPro数据集量化结果

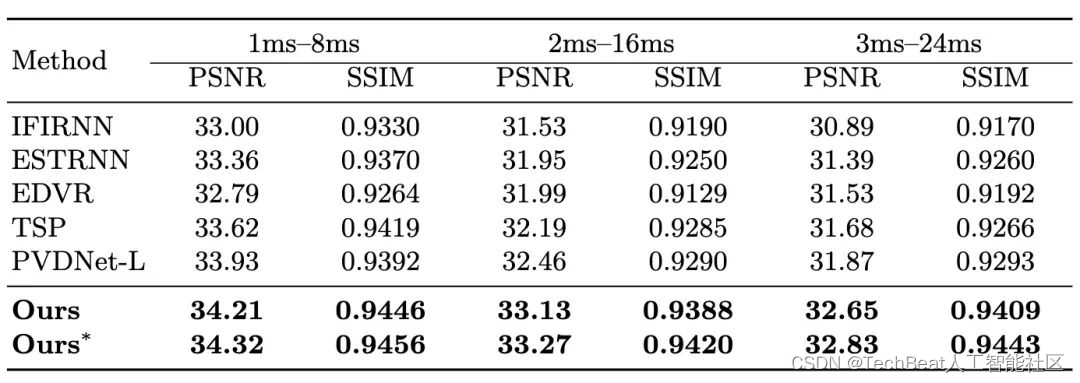
表3 BSD数据集量化结果

以下的视频展示了我们的方法和近期方法在BSD以及DVD数据集的对比结果。

四、总结

我们提出STDANet用于视频去模糊。这项工作的主要动机是，视频帧中并非所有的像素都是清晰和对去模糊有利的。因此，我们提出的STDANet通过考虑视频帧像素级的模糊程度来提取视频段中清晰像素的信息，从而更好的恢复出模糊中间帧。同时与主流的视频去模糊方法需要大型的光流网络进行运动估计不同，我们通过采用光流引导的方式进行帧间的运动补偿，因此我们可以使用一个非常轻量化的运动估计分支来进行粗略的光流估计，减小了计算量。在3个数据集的实验表明，我们的方法比起当前的sota方法，取得了更好的定量以及定性结果。

参考文献

[1] Online video deblurring via dynamic temporal blending network. In: ICCV (2017)

[2] Deep video deblurring for hand-held cameras. In: CVPR (2017)

[3] Cascaded deep video deblurring using temporal sharpness prior. In: CVPR (2020)

[4] Arvo: Learning all-range volumetric correspondence for video deblurring. In: CVPR (2021)

[5] Pwc-net: Cnns for optical flow using pyramid, warping, and cost volume. In: CVPR (2018)

[6] Deformable DETR: deformable transformers for end-to-end object detection. In: ICLR (2021)

-The End-

关于我“门”
▼

将门是一家以专注于发掘、加速及投资技术驱动型创业公司的新型创投机构，旗下涵盖将门创新服务、将门-TechBeat技术社区以及将门创投基金。

将门成立于2015年底，创始团队由微软创投在中国的创始团队原班人马构建而成，曾为微软优选和深度孵化了126家创新的技术型创业公司。

如果您是技术领域的初创企业，不仅想获得投资，还希望获得一系列持续性、有价值的投后服务，欢迎发送或者推荐项目给我“门”:

bp@thejiangmen.com