本文主要是介绍蓝桥杯螺旋折线(java实现),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
资源限制
内存限制:256.0MB C/C++时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s
如图所示的螺旋折线经过平面上所有整点恰好一次。
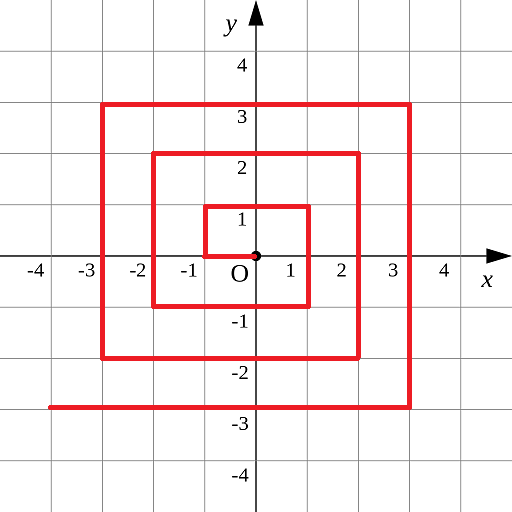
对于整点(X, Y),我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。
例如dis(0, 1)=3, dis(-2, -1)=9
给出整点坐标(X, Y),你能计算出dis(X, Y)吗?
输入格式
X和Y
对于40%的数据,-1000 <= X, Y <= 1000
对于70%的数据,-100000 <= X, Y <= 100000
对于100%的数据, -1000000000 <= X, Y <= 1000000000
输出格式
输出dis(X, Y)
样例输入
0 1
样例输出
3
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
注意:
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include <xxx>
不能通过工程设置而省略常用头文件。
提交程序时,注意选择所期望的语言类型和编译器类型。
开始解题:我的做法是把每个点分为上下左右四个部分,通过坐标就可以知道它是属于哪个部分。观察发现,上和下是由y值知道的,左和右是由x值知道的。而且还发现,当x=3,右部分边就有3条,而且还是单调递增公差为2首项为2的等差数列。所以,每种方向都可以看成是个等差数列,通过x或y值,就能知道那个有多少项,用求和公式就能算出每一部分的长度(所走路径)。当x=3,不能直接得出点在右边,还得看y的范围,观察发现,y的绝对值小于等于x的话,那么这个点肯定就在右边,同理,上下左右四个方向都可以按自己的规律,确定点是不是属于该方向。知道点在哪个方向后,我们就观察它此时,上下左右四个方向各有多少条边,比如点(-2,-3)在下面,y决定下面,所以有的绝对值3就是个关键数据,此时点要回到原点,就要走3个右边,3个上边,3个左边,这都是自己观察得出来的规律(再次强调,上下就和y有关,左右就和x有关)。它在下边,就先把当前边的距离算了,因为不完整嘛,然后再按方向,右、上、左、下,通过等差数列求和公式计算路径。所以解这个题就两步,1、确定方向,2、去相应方向里计算长度,因为每个方向的规律都不一样,都有自己的算法。
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);long x = in.nextLong();long y = in.nextLong();long length = 0;String flag = "";if (y < 0 && (x <= -y && x >= y - 1)) {flag = "down";} else if (x < 0 && (y <= -x && y >= x + 1)) {flag = "left";} else if (y > 0 && (Math.abs(x) <= y)) {flag = "up";}else {flag = "right";}switch (flag) {case "down":length += (-y-x);length += (-y * 2 + -y * (-y-1))*2;//上和右都是相同的等差数列,直接乘2length += (-y * -y)*2;break;case "left":length += (y-x-1);length += (-x * -x);length += ((-x-1) * -x)*2;length += ((-x-1)*(-x-1));break;case "up":length += (y + x);length += (y * y)*2;length += ((y - 1) * y)*2;break;case "right":length += (x - y);length += (x*x)*2;length += (x * (x + 1));length += ((x - 1) * x);break;}System.out.print(length);}
}这篇关于蓝桥杯螺旋折线(java实现)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





