本文主要是介绍Smart Use of Computational Resources Based on Contribution for Cooperative Coevolutionary Algorithms,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
0、论文背景
本文再DECC的基础上,提出了一种新的优化框架CBCC。在处理不可分离问题时,各种子成分对个体整体适应度的贡献之间通常存在不平衡。使用循环方式平等地对待所有的子组件,浪费计算预算。本文提出了一个基于贡献的合作协同进化(CBCC),它基于它们对全局适应度的贡献来选择子组件。这减轻了不平衡的问题,并允许更有效地利用计算资源。
Omidvar M N, Li X, Yao X. Smart use of computational resources based on contribution for cooperative co-evolutionary algorithms[C]//Proceedings of the 13th annual conference on Genetic and evolutionary computation. 2011: 1115-1122.
1、 不平衡问题
例如CEC2010的f4函数:
R是一个旋转矩阵来创建变量的交互作用;是1~n的随机排列向量;m设置为50,n设置为1000。f4包含50维不可分子分量和950维可分子分量,系数
造成了两个分量之间的不平衡,使不可分离的分量在整体适应度中具有更多的权重。
f4的随机初始化种群中,不可分子分量的平均适应度值约为;可分子分量的平均适应度值约为
。与不可分子分量相比,可分离子分量在全局适应度中的贡献可以忽略不计。因此优化这一类函数,CBCC根据子组件对提高整体适应度的贡献,贡献大的就选择子组件进行进一步优化。
2、分组策略
2.1 Delta分组
Delta分组是根据再前后两个周期每个维度的绝对变化大小对决策变量进行排序。将更有可能将具有相似增量值的交互变量彼此靠近。在一个CC框架中,变量的分组是根据排序后的增量值来确定的。
2.2 理想分组
理想分组是指将决策变量分解为一组子组件,其中任何两个子组件之间绝对没有相互依赖关系。这个得参照CEC2010得函数构造来看了,其中是需要我们从CEC2010的代码中知道的。
3、基于贡献的CC
提出了一种CBCC算法,通过测量各子分量进行优化时全局适应度的变化来估计每个子分量的贡献。分为两个阶段,测试阶段数组∆F跟踪所有子组件的适应度变化;优化阶段:选择∆F中条目最大的子组件进行进一步优化。
CBCC1在选择好子控件后只优化一次;而CBCC2在选择好子控件后,如果优化后的值有提升,则继续优化,否则转向测试阶段。

4、算法的复现以及简单实验
clc; clearvars; close all;
addpath('CEC2010\')
addpath('CEC2010\datafiles\');
addpath('CEC2010\javarandom\bin\');
addpath('CEC2010\javarandom\src\');
global initial_flagNS = 50; % 种群数
dim = 1000; % 种群维度
s = 20; % 子控件数目
upperBound = [100, 5, 32, 100, 5, 32, 100, 100, 100, 5, 32, 100, 100, 100, 5, 32, 100, 100, 100, 100];
lowerBound = [-100, -5, -32, -100, -5, -32, -100, -100, -100, -5, -32, -100, -100, -100, -5, -32, -100, -100, -100, -100];
bestYhistory = []; % 保存每次迭代的最佳值
bestfit1history = [];
bestfit2history = [];for funcNum = 4initial_flag = 0; % 换一个函数initial_flag重置为0sampleX = lhsdesign(NS, dim).*(upperBound(funcNum) - lowerBound(funcNum)) + lowerBound(funcNum).*ones(NS, dim); % 生成NS个种群,并获得其评估值lastSampleX = sampleX;[sampleY, fit1, fit2] = Copy_of_benchmark_func(sampleX, funcNum);[bestY, bestIndex] = min(sampleY); % 获取全局最小值以及对应的种群lastBestY = bestY;bestX = sampleX(bestIndex, :);bestYhistory = [bestYhistory; bestY];bestfit1history = [bestfit1history; fit1(bestIndex)];bestfit2history = [bestfit2history; fit2(bestIndex)];deltaF = zeros(1, s);version = 2;evalue = 1;while evalue < 2000 % 迭代50次if evalue == 1delta = zeros(1, dim);[~, index] = sort(delta);endfor i1 = 1 : sindex1 = index(((i1 - 1) * (dim / s) + 1) : (i1 * (dim / s)));subX = sampleX(:, index1);subX = SaNSDE(subX, sampleY, bestX, index1, 50, dim / s, lowerBound(funcNum), upperBound(funcNum), @(x)benchmark_func(x, funcNum));% 100*400sampleX(:, index1) = subX;[sampleY, fit1, fit2] = Copy_of_benchmark_func(sampleX, funcNum); % 100[bestY, bestIndex] = min(sampleY); % 获取全局最小值以及对应的种群bestX = sampleX(bestIndex, :);deltaF(1, i1) = deltaF(1, i1) + lastBestY - bestY;lastBestY = bestY;evalue = evalue + 1;enddelta0 = 1;while delta0 == 1 || delta0 / lastBestY > 0.01[~, index2] = max(deltaF);index1 = index(((index2 - 1) * (dim / s) + 1) : (index2 * (dim / s)));subX = sampleX(:, index1);subX = SaNSDE(subX, sampleY, bestX, index1, 50, dim / s, lowerBound(funcNum), upperBound(funcNum), @(x)benchmark_func(x, funcNum));% 100*400sampleX(:, index1) = subX;[sampleY, fit1, fit2] = Copy_of_benchmark_func(sampleX, funcNum); % 100[bestY, bestIndex] = min(sampleY); % 获取全局最小值以及对应的种群bestX = sampleX(bestIndex, :);delta0 = lastBestY - bestY;deltaF(1, index2) = deltaF(1, index2) + delta0;lastBestY = bestY;if version == 1delta0 = 0;endevalue = evalue + 1;endbestYhistory = [bestYhistory; bestY];bestfit1history = [bestfit1history; fit1(bestIndex)];bestfit2history = [bestfit2history; fit2(bestIndex)];delta = sum(abs(sampleX - lastSampleX),1) ./ NS;% delta = sum(sampleX - lastSampleX,1) ./ NS;[~, index] = sort(delta);lastSampleX = sampleX;disp(evalue);end
end
figure(1);
plot(bestYhistory);
hold on;
plot(bestfit1history);
hold on;
plot(bestfit2history);
save('CCBC_DY.mat','bestYhistory');
save('CCBC_Dfit1.mat','bestfit1history');
save('CCBC_Dfit2.mat','bestfit2history');
legend('Y','fit1','fit2','Location', 'northeast');f4的Y值对比:
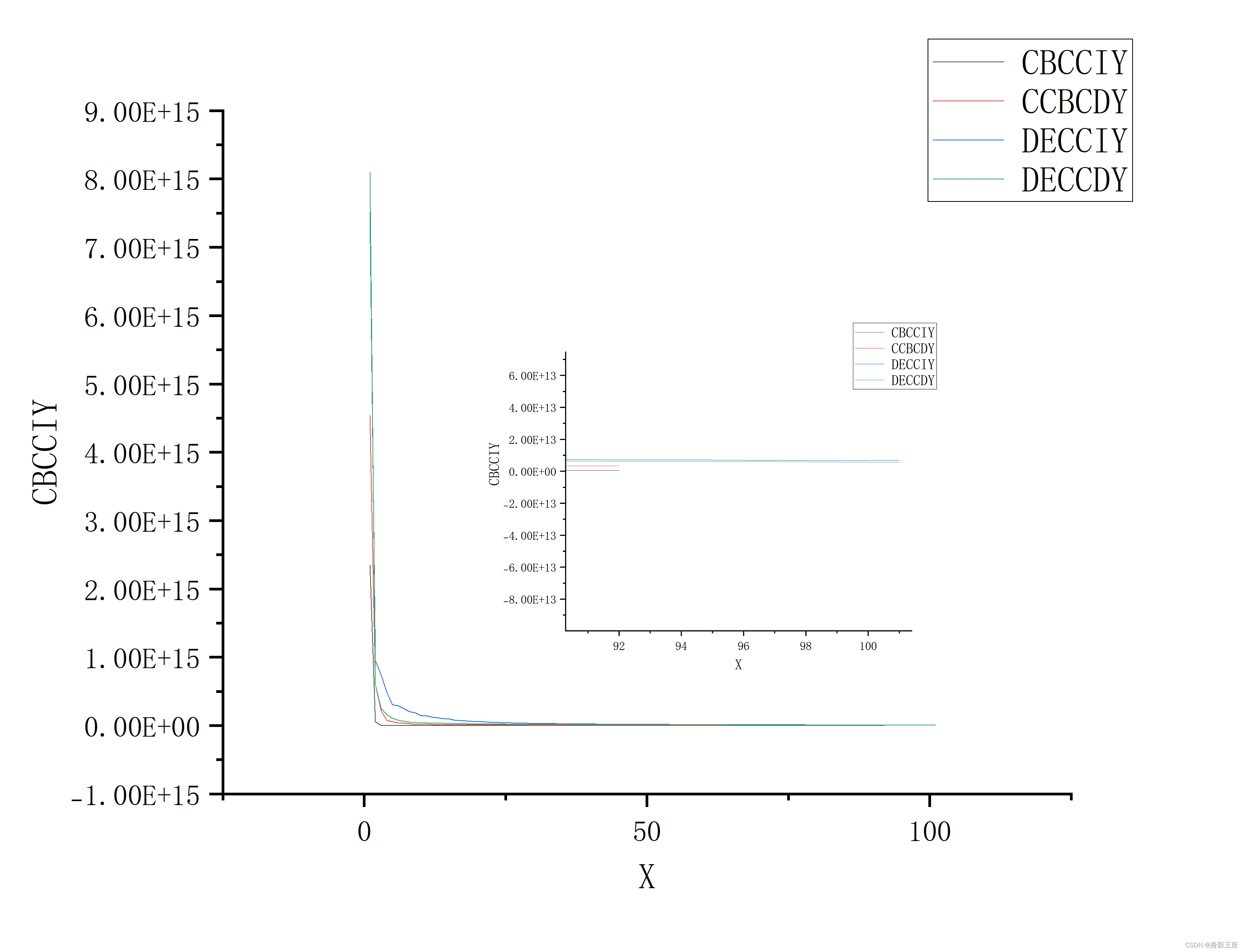
可以看到CCBC优化效果好于DECC。
f4的fit1值对比:
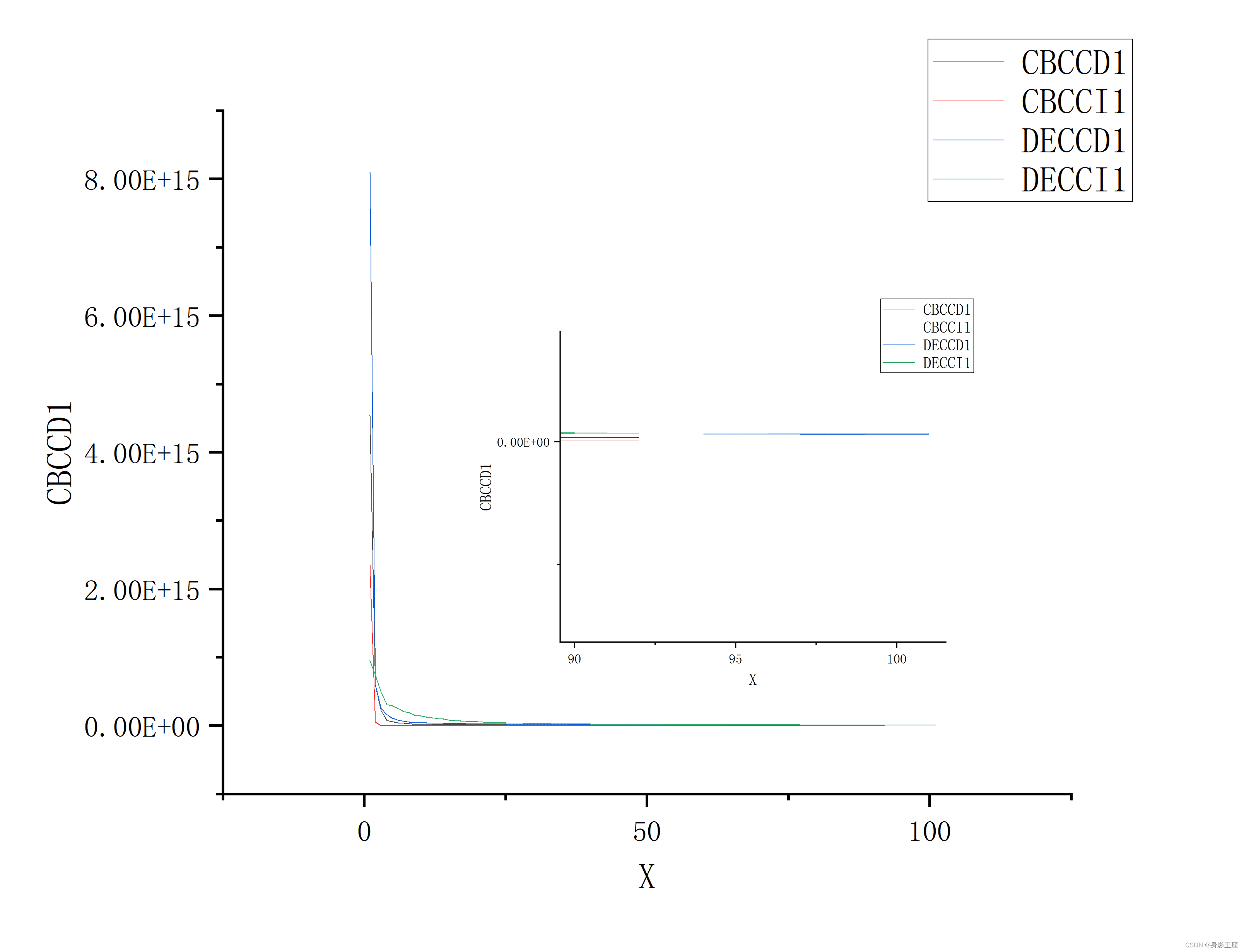
也和上述结论差不多。
f4的fit2值对比:
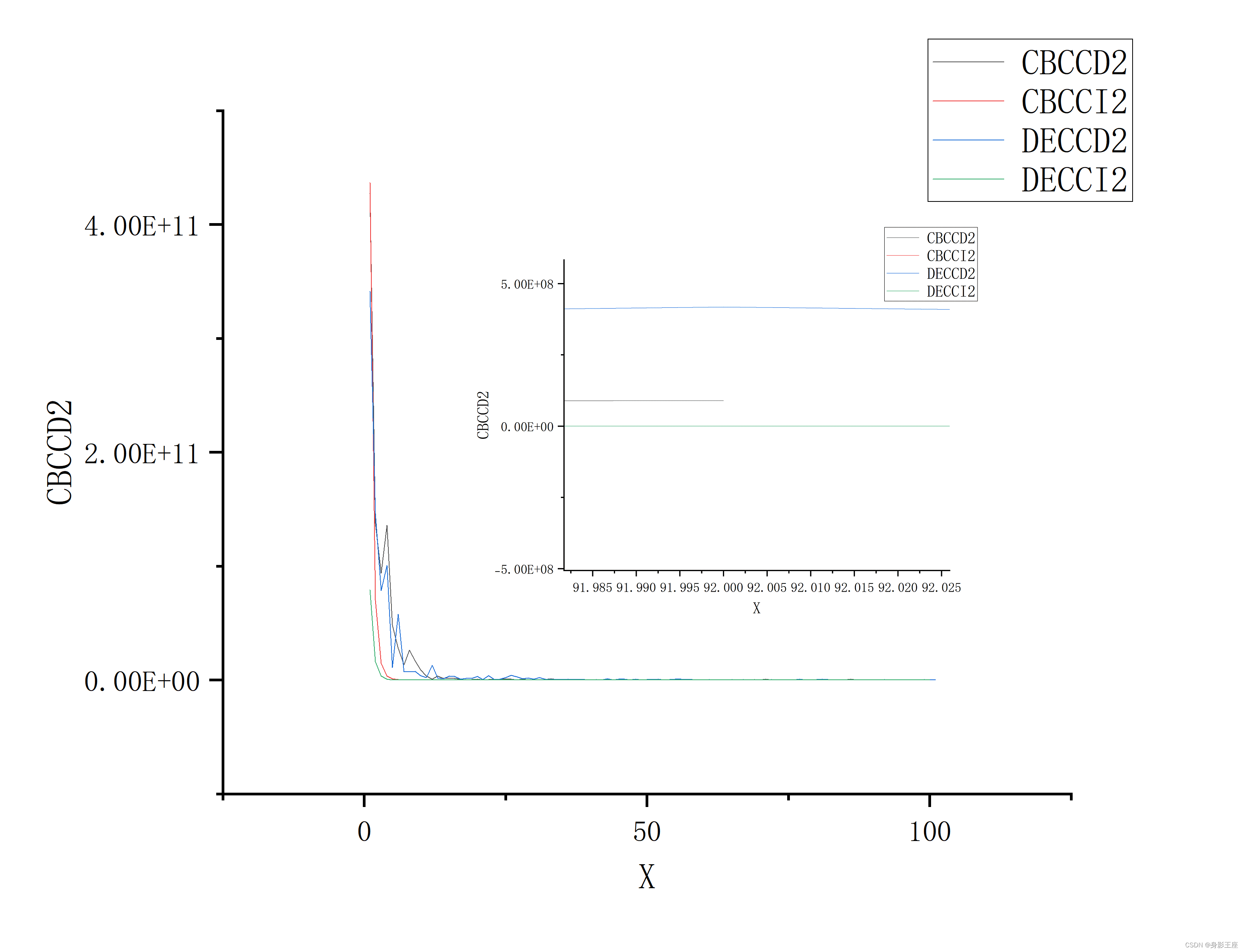
Delta分解会有上下波动,说明 Delta分解不能将变量完全分为可分解部分和不可分解部分;而Delta分解得到的结果是没有理想分解好的。
如有错误还请批评指教!
这篇关于Smart Use of Computational Resources Based on Contribution for Cooperative Coevolutionary Algorithms的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







