c++数据结构实验 图与景区 (借鉴须谨慎)

本文主要是介绍c++数据结构实验 图与景区 (借鉴须谨慎)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

丑话说在前头，由于不可控原因，本实验与老师建议的形式略有差异(少了两个文件），如果担心因此降低实验课分数的，建议只是借鉴一下。
好久没写博客了，放寒假回去摸了好久。近几天才回过神来，开始认真做实验。

实验

源码

Main.cpp

#include<iostream>
#include"Graph.h"
using namespace std;int main(void)
{int choose;Graph *graph=new Graph();while (true){//输出界面cout << "====景区信息管理系统====" << endl;cout << "1.创建景区景点图" << endl;cout << "2.查询景点信息" << endl;cout << "3.旅游景点导航" << endl;cout << "4.搜索最短路径" << endl;cout << "5.铺设电路规划" << endl;cout << "0.退出" << endl;cout << "请输入操作编号(0-5):";cin >> choose;switch (choose){case 1: {graph->CreateGraph();break;}case 2: {graph->GetSpotInfo();break;}case 3:graph->DFSTravers();break;case 4:graph->FindShortPath();break;case 5:graph->FindMinTree();break;case 0:return 0;default:cout << "请输入正确编号!" << endl;}}return 0;
}

Graph.h

#pragma once
#ifndef GRAPH_H
#define GRAPH_Hstruct Vex
{int num;  //景区编号char name[20];  //景区名字char desc[1024];  //景点介绍
};struct Edge
{int vex1;   //边的第一个顶点int vex2;   //边的第二个顶点int weight;  //权值
};typedef struct PathList  
{int vexs[20];   //保存一条路径PathList* next;  //下一条路径
}*Path;class Graph
{
private:int Map[20][20];  //邻接矩阵Vex Vexs[20];   //顶点信息数组int VexNum;   //当前图的顶点个数
public:Graph();~Graph();void Init(void);  //初始化图bool InsertVex(Vex sVex);  //插入顶点信息bool InsertEdge(Edge sEdge); //插入边信息Vex GetVex(int v);   //显示景点信息int FindEdge(int v, Edge aEdge[]);  //查询相邻景点int CreateGraph(void);  //读取文件，创建景点图int GetVexNum();      //获取景点数量void GetSpotInfo(void);    //获取所有顶点信息void DFS(int v, bool Visited[], int& Index, Path& path);  //深度优先void DFSTravers();                 int FindShortPath();           //最短路径int FindMinTree();         //电路规划 最小生成树
};#endif 

Graph.cpp

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<fstream>
#include"Graph.h"
using namespace std;
#define INF 65535Graph::Graph()
{}Graph::~Graph()
{}void Graph::Init(void)
{for (int i = 0; i < 20; i++) {for (int j = 0; j < 20; j++) {if (i == j) {Map[i][j] = 0;}else {Map[i][j] = 0xffff;}}}VexNum = 0;
}bool Graph::InsertVex(Vex sVex)
{if (VexNum >= 20){return 0;}Vexs[VexNum] = sVex;VexNum++;return 1;
}bool Graph::InsertEdge(Edge sEdge)
{int num1 = sEdge.vex1;int num2 = sEdge.vex2;if (num1 != num2){Map[num1][num2] = sEdge.weight;Map[num2][num1] = sEdge.weight;return 1;}return 0;
}Vex Graph::GetVex(int v)
{return Vexs[v];
}int Graph::FindEdge(int v, Edge aEdges[])
{int k = 0;for (int i = 0; i < VexNum; i++){if (Map[i][v] > 0 && Map[i][v] < 0xffff){aEdges[k].vex1 = v;aEdges[k].vex2 = i;aEdges[k].weight = Map[i][v];k++;}}return k;
}//读取文件，创建景区景点图
int  Graph::CreateGraph(void)
{cout << "=====创建景区景点图=====" << endl;ifstream is;is.open("D:\\Desktop\\Vex.txt");   //绝对路径，注意 "\\"if (!is){cout << "Vex.txt文件打开失败!" << endl;return 0;}int n;is >> n;cout << "顶点数目:" << n << endl;;VexNum = n;Init();   //初始化图cout << "----- 顶点 -----" << endl;for (int i = 0; i < n; i++){Vex vex;is >> vex.num >> vex.name >> vex.desc;cout << vex.num << "-" << vex.name << endl;if (InsertVex(vex) == 0){cout << "读取顶点文件信息失败！" << endl;is.close();return 0;}}is.close();is.open("D:\\Desktop\\Edge.txt");Edge edges[190];int k = 0;cout << "----- 边 -----" << endl;while (is >> edges[k].vex1 >> edges[k].vex2 >> edges[k].weight){cout << "<v" << edges[k].vex1 << ",v" << edges[k].vex2 << ">" << edges[k].weight << endl;if (InsertEdge(edges[k]) == 0) {cout << "读取边文件信息失败！" << endl;is.close();return 0;}k++;}for (int i = 0; i < k; i++){int num1 = edges[i].vex1;int num2 = edges[i].vex2;int weight = edges[i].weight;Map[num1][num2] = weight;Map[num2][num1] = weight;}is.close();cout << "成功创建景区景点图" << endl;return 0;
}int Graph::GetVexNum()
{return VexNum;
}void Graph::GetSpotInfo(void)
{cout << "===== 查询景点信息 =====" << endl;for (int i = 0; i < VexNum; i++){cout << Vexs[i].num << "-" << Vexs[i].name << endl;}int choose;cout << "请输入想要查询的景点信息:";cin >> choose;cout << Vexs[choose].name << endl;cout << Vexs[choose].desc << endl;Edge edges[20];cout << "----- 周边景区 -----" << endl;int edgeNum=FindEdge(Vexs[choose].num,edges);for (int k = 0; k < edgeNum; k++){cout << "<v" << edges[k].vex1 << ",v" << edges[k].vex2 << ">" << edges[k].weight << endl;}}//v 起始点编号  Visited 标记景点是否已访问  Index 遍历深度
void Graph::DFS(int v, bool Visited[], int& Index, Path& path)
{Visited[v] = true;   //起始点已访问path->vexs[Index++] = v;int num = 0;   //访问过的结点数for (int i = 0; i < VexNum; i++){if (Visited[i]) {   //已访问，则加一num++;}}if (num == VexNum)  //全访问过{/*错误示范  如此操作会导致只能存储最后一条路径，前面得到的路径都被覆盖，path.next后为NULLpath->next = new PathList;path = path->next;path->next = NULL;*/path->next = new PathList;for (int i = 0; i < VexNum; i++)  //获得一条路线之后，会再次递归(以原 path 为参数){path->next->vexs[i] = path->vexs[i];   //将path中得到的一条路径信息复刻到新的path中}path = path->next;path->next = NULL;}else {for (int i = 0; i < VexNum; i++){if (Map[i][v] != 0&&Map[i][v]!=0xffff && !Visited[i])   //邻接点(条件要写全) 未访问{DFS(i, Visited, Index, path);   //递归调用DFSVisited[i] = false;        //改为未访问Index--;   //索引值减一}}}
}void Graph::DFSTravers()
{cout << "===== 景区景点导航 =====" << endl;for (int i = 0; i < VexNum; i++){cout << Vexs[i].num << "-" << Vexs[i].name << endl;}int choose;cout << "请输入起始点编号:";cin >> choose;Path path=new PathList;Path head = path;int Index = 0;bool Visited[20] = { false };DFS(choose, Visited, Index, path);cout << "导航路线为:" << endl;int i = 1;path = head;while (path->next != NULL){Vex vex = GetVex(path->vexs[0]);cout << "路线" << i++ << ":" << vex.name;for (int j = 1; j < VexNum; j++){vex = GetVex(path->vexs[j]);cout << "->" << vex.name;}cout << endl;path = path->next;}cout << endl;delete path;path = NULL;head = NULL;
}int Graph::FindShortPath()
{cout << "===== 搜索最短路径 =====" << endl;for (int i = 0; i < VexNum; i++){cout << Vexs[i].num << "-" << Vexs[i].name << endl;}int nVexStart, nVexEnd;Edge aPath[20];cout << "请输入起点的编号:";cin >> nVexStart;cout << "请输入终点的编号:";cin >> nVexEnd;//初始化最短路径//标记数组 ，前置顶点int flag[20] = { 0 };   //默认为未置入集合int	pre[20] = {-1}; int dist[20], k;   //distance 距离for (int i=0;i<VexNum;i++){if (Map[nVexStart][i] > 0 || i == nVexStart){dist[i] = Map[nVexStart][i];   //两点距离pre[i] = nVexStart;  //当两个边直接相连时，pre初始化为起点}else {dist[i] = INF;}}/*for (int i = 0; i < VexNum; i++){if (dist[i] != INF) {cout << "dist[" << i << "]:" << dist[i] << endl;}}cout << endl;*/flag[nVexStart] = 1;int min;//每次找出一个顶点的最短路径for (int i = 1; i < VexNum; i++){min = INF;for (int j = 0; j < VexNum; j++){if (flag[j] == 0 && dist[j] < min){min = dist[j];k = j;        //最短路径的点}}flag[k] = 1;if (k == nVexEnd)  //k为终点{break;}//以k为中间点，计算nVexStart到所有顶点的最短路径for (int j = 0; j < VexNum; j++){int tmp;if (Map[k][j] == 0) {tmp = INF;}else {tmp = min + Map[k][j];}if (flag[j] == 0 && tmp < dist[j]){dist[j] = tmp;pre[j] = k;}}/*检错时用for (int i = 0; i < VexNum; i++){if (dist[i] != INF) {cout << "dist[" << i << "]:" << dist[i] << endl;}}cout << endl;*/}/*检错时用for (int i = 0; i < VexNum; i++){if (dist[i] != INF) {cout << "pre[" << i << "]:" << pre[i] << endl;}}cout << endl;*/cout << "最短路线为:";int distance = 0;distance = dist[nVexEnd];//下面的有点绕 捉住 Num 好理解一点int Num = 0;  int i = nVexEnd;while (i != nVexStart){aPath[Num].vex2 = i;   //后结点 vex2:4 aPath[Num].vex1 = pre[i];  // 前结点 vex1:3  aPath[Num].weight = Map[i][pre[i]];i = pre[i];Num++;}//cout<<Num<<endl;//开始编号：1  结束编号: 4//最短路径：1->2->3->4//Num=3for (i = Num - 1; i >= 0; i--){cout << Vexs[aPath[i].vex1].name << "->";}i++;cout <<Vexs[aPath[i].vex2].name<<endl;cout << "最短距离为"<<distance<<endl;return 0;
}/*对于同一个图，得到多个最小生成树的方式有两种：
(1) 改变顶点的查找顺序
(2) 当有多条权值最小的边时，使用栈将每条边都保存下来
*///构建最小生成树  prim算法
int Graph::FindMinTree()
{cout << "===== 铺设电路规划 =====" << endl;Edge aPath[20];int TV[20] = {1000};int num = 0;TV[0] = 0;      //默认景点0-A区为起点int flag[20] = { 0 };int closest = 10000;int signal_1;int signal_2;int distance = 0;flag[0] = 1;signal_1 = 0;int i, j, k;//将剩余景点(VexNum-1)置入TV[]中for (i = 1; i < VexNum; i++){for (j = 0; j <= num; j++){for (k = 0; k < VexNum; k++){if (flag[k]==0&&Map[k][TV[j]] <= closest){closest = Map[k][TV[j]];signal_1 = j;signal_2 = k;}}}flag[signal_2] = 1;         //注意，此处的 signal_2 不能与 k 弄混//cout << "flag[" << signal_2 << "]:" << flag[signal_2]<<endl;aPath[num].vex1 = signal_1;aPath[num].vex2 = signal_2;aPath[num].weight = closest;distance += closest;TV[++num] = signal_2;/*检错时用的for (i = 0; i < num; i++){cout << Vexs[aPath[i].vex1].name << " - " << Vexs[aPath[i].vex2].name << "  " << aPath[i].weight << endl;}cout << endl;*/closest = 10000;      //不可少！}cout << "在以下两个景区之间铺设电路:" << endl;for (i = 0; i < num; i++){cout << Vexs[aPath[i].vex1].name << " - " << Vexs[aPath[i].vex2].name << "  " << aPath[i].weight << endl;}cout << "铺设电路的总长度为:" << distance<<endl;return 0;}

成果

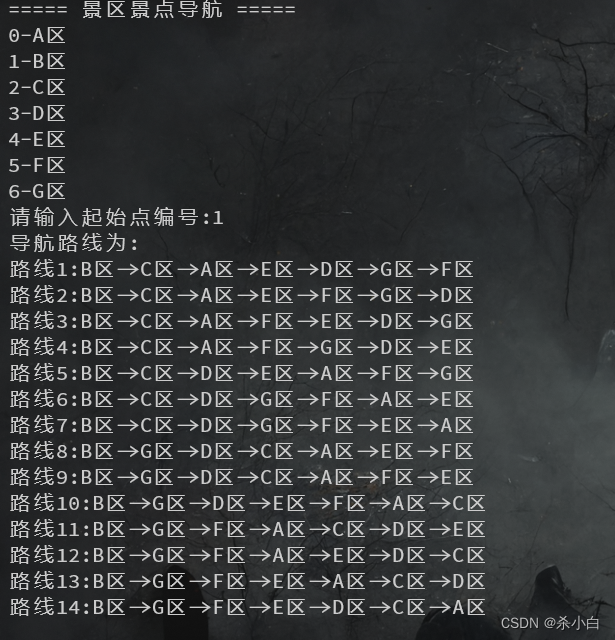
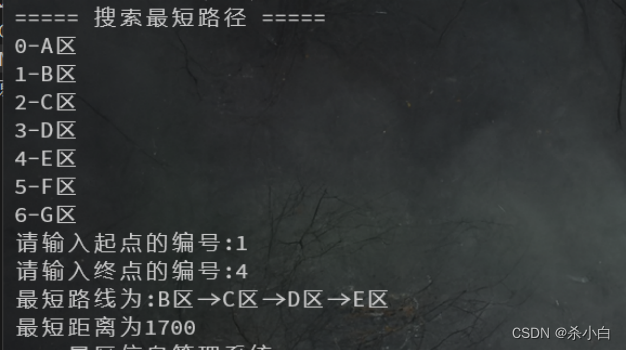
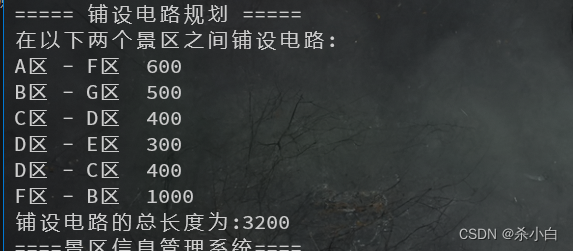
结尾

最后聊一下本次实验为啥与老师建议的有所不同。其实是过完年回来，回到学校摆了差不多一个月。而本次实验开学第一周就开始了。第一和第二周我没听课，就随便找网上的敷衍一下。第三周，之前找的那个没写到，我就又找别的代替了，也没运行过(记性差，忘记快捷键了，那时懒得找)。
到后面实在玩腻了，开始动手时，发现前后找的两篇文章的代码不适配(当时就裂开了)。后面没办法，又不想删掉重写，就硬着头皮，主要以第一篇文章的基础，参考第二篇文章的思想，废了好大功夫才续写成功。

这篇关于c++数据结构实验 图与景区 (借鉴须谨慎)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---