LeetCode 0310.最小高度树：拓扑排序秒了

本文主要是介绍LeetCode 0310.最小高度树：拓扑排序秒了，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【LetMeFly】310.最小高度树：拓扑排序秒了

力扣题目链接：https://leetcode.cn/problems/minimum-height-trees/

树是一个无向图，其中任何两个顶点只通过一条路径连接。 换句话说，一个任何没有简单环路的连通图都是一棵树。

给你一棵包含 n 个节点的树，标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。

可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h 。在所有可能的树中，具有最小高度的树（即，min(h)）被称为 最小高度树 。

请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。

树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。

 

示例 1：

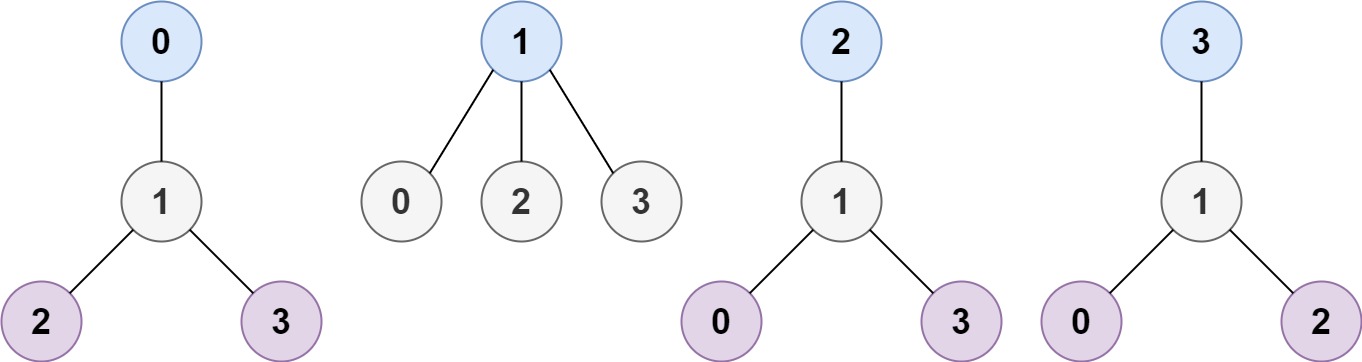
输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。

示例 2：

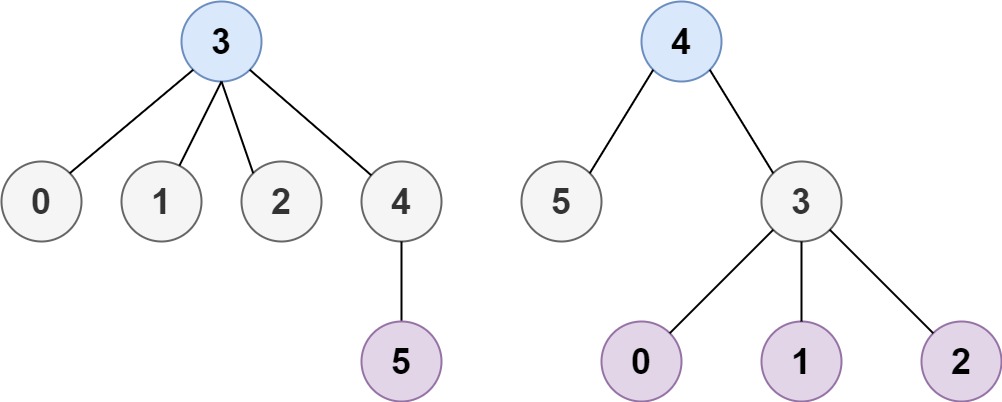
输入：n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出：[3,4]

 

提示：

• 1 <= n <= 2 * 104
• edges.length == n - 1
• 0 <= ai, bi < n
• ai != bi
• 所有 (ai, bi) 互不相同
• 给定的输入 保证 是一棵树，并且 不会有重复的边

方法一：拓扑排序

根据图论我们知道，（非空）树的中心有一个或两个。

原因小提示：

树中最长路的中心有一个或两个。

那么，我们来个拓扑排序不就好了？

从叶节点开始“扔”，每次扔掉所有的叶节点节点。这样就会出现新的叶节点，再扔掉。…。一层一层，直到某层扔完时剩下一个或两个节点即为答案。

拓扑排序怎么实现：

使用一个数组degree，degree[i]表示与节点i相邻的边有几条，图论中称其为度。

初始时将所有度为1的节点入队。

每次将这一层的所有节点出队，对于出队的节点thisNode，它的所有相邻的节点的度减一。若度变成了1，则入队（新的叶节点get）。

• 时间复杂度$O(n)$
• 空间复杂度$O(n)$

AC代码

C++

class Solution {
public:vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {if (n == 1) {  // 这里不要忘了！要不然degree不为1return {0};}vector<int> degree(n);vector<vector<int>> graph(n);for (vector<int>& v : edges) {degree[v[0]]++;degree[v[1]]++;graph[v[0]].push_back(v[1]);graph[v[1]].push_back(v[0]);}queue<int> q;for (int i = 0; i < n; i++) {if (degree[i] == 1) {q.push(i);}}int remainNode = n;while (remainNode > 2) {for (int _ = q.size(); _ > 0; _--) {remainNode--;int thisNode = q.front();q.pop();for (int nextNode : graph[thisNode]) {degree[nextNode]--;if (degree[nextNode] == 1) {q.push(nextNode);}}}}vector<int> ans = {q.front()};q.pop();if (q.size()) {ans.push_back(q.front());}return ans;}
};

Python

from typing import Listclass Solution:def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:if n == 1:return [0]degree = [0] * ngraph = [[] for _ in range(n)]for x, y in edges:degree[x] += 1degree[y] += 1graph[x].append(y)graph[y].append(x)q = [i for i, d in enumerate(degree) if d == 1]remainNode = nwhile remainNode > 2:tempQ = []for thisNode in q:remainNode -= 1for nextNode in graph[thisNode]:degree[nextNode] -= 1if degree[nextNode] == 1:tempQ.append(nextNode)q = tempQreturn q

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/136790299

这篇关于LeetCode 0310.最小高度树：拓扑排序秒了的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---