代码随想录算法训练营day59|第十章 单调栈part02

本文主要是介绍代码随想录算法训练营day59|第十章 单调栈part02，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

503.下一个更大元素II 

42. 接雨水  

503.下一个更大元素II 

vector<int> nextGreaterElements(vector<int>& nums) {stack<int> st;vector<int> res(nums.size(),-1);st.push(0);for(int i=1;i<nums.size()*2-1;i++){while(st.size()&&nums[i%nums.size()]>nums[st.top()]){res[st.top()]=nums[i%nums.size()];st.pop();}st.push(i%nums.size());}return res;}

这道题使用双指针的思路其实是遍历两遍height数组，分别找到它的右边最高的柱子和左边最高的柱子，然后取这两个的最小值，这个值就是填满水之后应该达到的高度，如果这个高度是正值那就加上，反之说明不合法则不予理会，以此来求当前下标处增加的水量。

遍历求右边最高柱子的时候要从右往左遍历，如果当前的柱子高度小于历史最高柱子的高度，那就把历史最高柱子高度赋值给它，反之如果大于，那就证明当前柱子的右边没有比它更高的柱子了，于是这个下标处也不会盛水，所以为了依旧套用递推公式，这个地方应该赋值为当前柱子的高度(在使用递推公式推导的时候，需要求最小值，这个最小值有可能是当前柱子的高度，那么计算出来值就会是0，而如果是最左边柱子的高度，那么这个值就会是负数，而因为不合法，所以不被加入)。于是推导公式就简化为取当前柱子高度和历史柱子最高高度的最大值。求左边最高柱子数组差不多一个道理，只是需要倒序遍历。注意，可以事先设置这个最大高度为0，然后遍历就可以从两端开始，或者也可以直接把两端的值设置为两端柱子的高度，这样可以少遍历一个值，其实大差不差。

int trap(vector<int>& height) {if (height.size() <= 2) return 0;vector<int> maxLeft(height.size(), 0);vector<int> maxRight(height.size(), 0);int size = maxRight.size();// 记录每个柱子左边柱子最大高度maxLeft[0] = height[0];for (int i = 1; i < size; i++) {maxLeft[i] = max(height[i], maxLeft[i - 1]);}// 记录每个柱子右边柱子最大高度maxRight[size - 1] = height[size - 1];for (int i = size - 2; i >= 0; i--) {maxRight[i] = max(height[i], maxRight[i + 1]);}// 求和int sum = 0;for (int i = 0; i < size; i++) {int count = min(maxLeft[i], maxRight[i]) - height[i];if (count > 0) sum += count;}return sum;}

这道题使用单调栈做法也比较复杂，因为单调栈每次会弹出一些元素，所以不能像双指针做法那样按列来求，而是要一行一行的求，也就是除了求增加水量的高度之外，还要求增加水量的宽度(上一题直接求高度代表水量是因为宽度默认为1了)。

每次如果遍历到大于栈顶元素的值，那就先记录一下当前的栈顶元素，然后再弹出这个栈顶元素，然后再判断一下这个栈里面是否还剩有元素，如果剩有元素，证明可能构成一个凹槽用来盛水，那就要计算盛水的水量，先计算水的高度，水的高度取遍历的柱子的高度和栈顶高度的最小值再减去之前储存的那个栈顶元素，水的宽度当然就是遍历的元素的下标和现在栈顶元素的下标的下标差再减一(因为求的是中间的部分，用来盛水的那种宽度)，相乘求得水量；而如果没有元素剩余，那就证明不能盛水。无论能否盛水，都需要将当前元素压入栈，以便后来的判断。如果遍历到小于等于栈顶元素的值，那就直接压入栈。

其实便利到等于栈顶元素的值有两种处理方法，第一种方法是直接压入栈中，然后按上面的做法来处理；另一种做法是舍弃掉这个元素，其实就算不舍弃压入栈中，最后公式计算得到的增加水量也是零，所以没什么太大差别。

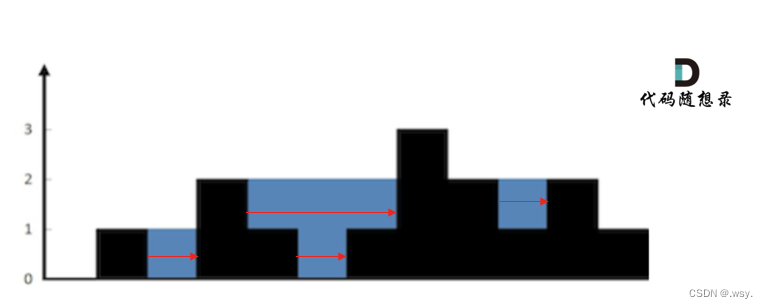
int trap(vector<int>& height) {stack<int> st;st.push(0);int sum = 0;for (int i = 1; i < height.size(); i++) {while (!st.empty() && height[i] > height[st.top()]) {int mid = st.top();st.pop();if (!st.empty()) {int h = min(height[st.top()], height[i]) - height[mid];int w = i - st.top() - 1;sum += h * w;}}st.push(i);}return sum;}

这篇关于代码随想录算法训练营day59|第十章 单调栈part02的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！