本文主要是介绍【考研数学】660/880/1000/1800 使用手册,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
开门见山,直接介绍几个热门的习题册
660:660表面上叫基础通关660,但实际上很多题的难度并不适合基础阶段,建议在强化阶段搭配着 严选题做660,对提升做小题的速度和能力非常有帮助。
880:题量适中,难度适中,题目比较常规,有些新的点,没有很多偏题怪题。如果大家做880,建议强化阶段使用。
1000题:现在的 1000 题是把每个知识点按 A、B、C 进行分类,把同一类型整合在一起,难度按组逐渐提升,较比之前的笼统排版来说,适应性很强,题型部分也比较全面。
1800:分为基础篇和拔高篇,难度按梯次分配适中。其中基础篇的题目尤其好,非常适合基础阶段一般的同学,而且每个章节包含了入门和基础,囊括了选择、填空和解答等多题型,题型的覆盖范围非常广,能帮助大家在初期打下扎实的基础,不用担心强化阶段出现基础不牢,地动山摇的情况。
如果选择1000,1800类的习题册,从题量来说,一本就可以满足,甚至1800不用全部做完,选择其中一部分,做精做透得一个好成绩不是问题。
如果选660的话,做完后能获得一个扎实的基础,但是题量可能有些不足,覆盖不全面,推荐加上880做一个组合,两者算一个不错的搭配。
强化阶段1000左右的题量就足够了,但一定要在做题之后总结出各知识点常见题型及其解法,熟练掌握。
最后冲刺阶段加上真题+模拟题的练习。
总体上说,按照自己的喜好,课程选择适合自己的习题册,不要过分所谓的“好”。

我算是从零开始,因为长时间没有学习高数,几乎所有的知识点都遗忘了。
一开始还走了不少弯路,幸好后来找到了正确的备考方法,最终数学考了令我满意的 119 分,一次就成功上岸了。
希望我的经验能帮助你避免我曾经踩过的坑,顺利上岸。
全文超过 1 万字,包括如何有效规划备考时间,选择老师和资料。建议收藏,因为在后续备考过程中它一定会帮到你。
一、资料与视频
我在备考期间使用的学习资料包括:
汤家凤的基础课视频+1800题、660题、以及近20年真题和李林的4+6模拟卷。
软件:「知能行考研数学」:知能行数二一共有18个专题,我将其中8个专题刷到了等级3,即真题水平。
1、基础视频+1800题
在基础阶段,我选择了汤家凤老师的视频课,他的授课风格非常沉稳。当然,缺点是有时会显得过细,让人有点犯困 😅
然而,如果你是零基础,我建议你务必认真听一下老汤的基础课。我最喜欢的是老汤在讲课时会在纸上写下所有的知识点,对于刚入门的初学者来说非常友好。
因为我观看的是汤家凤老师的基础课视频,所以我边看视频边做1800题。

但是,我开始做1800题的时候很崩溃,实在无法坚持下去,习题册和视频之间有些脱节,有些知识点好像没有在视频中讲解过,有些讲解了,但我却无法做题。
而且我发现在1800题中,有许多题目都考察相同的知识点,但在做题前我并不知道哪些题目是属于相同知识点的,这导致效率很低,我觉得这一点非常不友好。因此,我停止做了一段时间的1800题,转而做李永乐的660题。
2、基础过关660题
做660题的时候情况更加严峻,我没有想到尽管名字中带有“基础练习”,我却做得如此吃力。
我完全没有思路,只能死磕答案,一个上午浪费在一道题上。这样的刷题过程真的非常痛苦...
这对我的信心打击很大,一度让我想要放弃考研。

事实上,660题并不是基础题,它考察的是对“基础知识”的综合运用。它总能以你意想不到的方式出题,对基础知识的考察非常细致,几乎无所不包,并且是综合性考察。
自从21年大纲改革以来,客观题的比重大幅上升,660题确实有必要做一做,但是死磕660题并不是明智的选择。
二、高效备考的利器
在被660题击垮后,我意识到继续只看视频会很糟糕,于是开始在网上寻找备考经验。 当我在知乎搜索考研数学内容时,意外发现了「知能行考研数学」。一开始我以为它只是一个在线题库,但使用了一段时间后才意识到它的强大之处。

这是传送门:
知能行考研数学知能行考研数学通过大数据分析历年真题的考点难点,为每位考生选择快速提高的突破口。知能行基于机器学习追踪考生知识点的掌握情况,测练合一从而达到高效备考![]() https://bestzixue.com/?app_referrer_id=7F2~atczc-mathBooks-0310-editor_leigao
https://bestzixue.com/?app_referrer_id=7F2~atczc-mathBooks-0310-editor_leigao

我发现知能行会根据我的做题情况,逐步选择适合我的题目,直到我能够熟练掌握,不断完善我的知识结构。
当我遇到不会的题时,知能行会逐步分析我的薄弱知识点,通过逐层剖析错误原因,一步步找出基础薄弱的问题,并推荐相应的题目进行强化巩固。

因此,在使用znx刷题过程中,我逐渐构建了一个循序渐进的知识结构,然后通过持续的强化和综合测试,形成了正向反馈的闭环。
这种学习方式让我对学习产生了新的想法,即只通过刷题来学习考试中的知识点。
我放弃了大部分时间观看视频。当时为了赶上刷题进度,我尝试了这种方法,最终成绩还不错,证明这种方法是可行的。
前提是要通过自己做题来理解题目中的知识点,如果遇到特别难理解的题目,再去有针对性地观看视频,可以节省很多时间。
知能行全面覆盖了考研大纲中的所有知识点。在使用过程中,后台算法会根据我的个人刷题情况生成我专属的练习册,给我制定一条专属的学习路线。

因此,我决定改变备考策略,全面采用知能行来复习考研数学。我一边刷题,一边学习znx的「复习要点」,通过题目补充基础知识。这大大提高了复习效率。

给你整理好的知识框图

知能行每个专题都有等级,等级3满分达到真题水平。
在使用知能行的过程中,经常会有一种闯关的体验,让我感觉上瘾!看着进度条不断上涨,确实能感受到自己的能力在逐步提高,这真的很有动力!

我觉得知能行最棒的一点是每天的综合测试。它不仅能找到当前的薄弱点进行巩固,还能让我每天保持做数学题的手感。这相当于每天进行一次小型的数学模拟考试。
纸质练习册的反馈效果很不好,只能通过正确率简单判断掌握情况,却无法具体评估知识点掌握情况。
这时通过知能行就可以实时了解到每个知识点的掌握情况,滚动复习。重要的是,它根据你的薄弱点出新题,不断巩固加深,这对于后期时间紧张时不会因为其他科目而遗忘,是非常关键的。
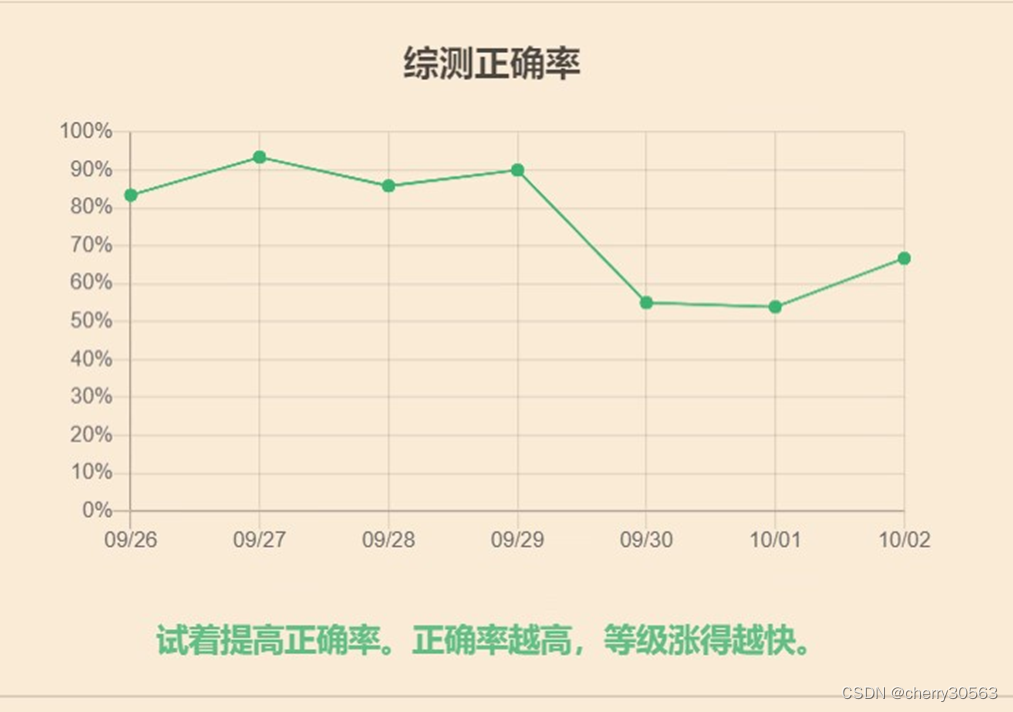
实时查看你的每日进度
我非常喜欢这个功能,它可以直观地显示出我每天做了多少题,正确率如何。我们可以看到正确率的变化趋势,清晰地了解自己是否有进步。
你的专属能力图
有了这个能力图,你就可以直观地了解自己哪方面存在薄弱项。比如,如果你的基础功力不行,在图中一眼就能看出来,然后你可以有针对性地加强基础功力。最终,你将成为一个全面发展、无所不能的“等边三角形战士”。

在我的记忆中,刷数学题一直是一件痛苦的事情,就像660题给我带来的阴影一样。但知能行彻底改变了我对考研数学的看法,它强大的正向反馈和每次训练后的进步成就感,常常让我刷题刷得停不下来!
三:时间安排
指导方针
注重打好基础,坚持变中求稳。
循序渐进,避免急躁。
脚踏实地,勤思勤算。
知能行根据不同的习题册制定刷题计划,时间具体到小时,非常适合搭配习题集使用。
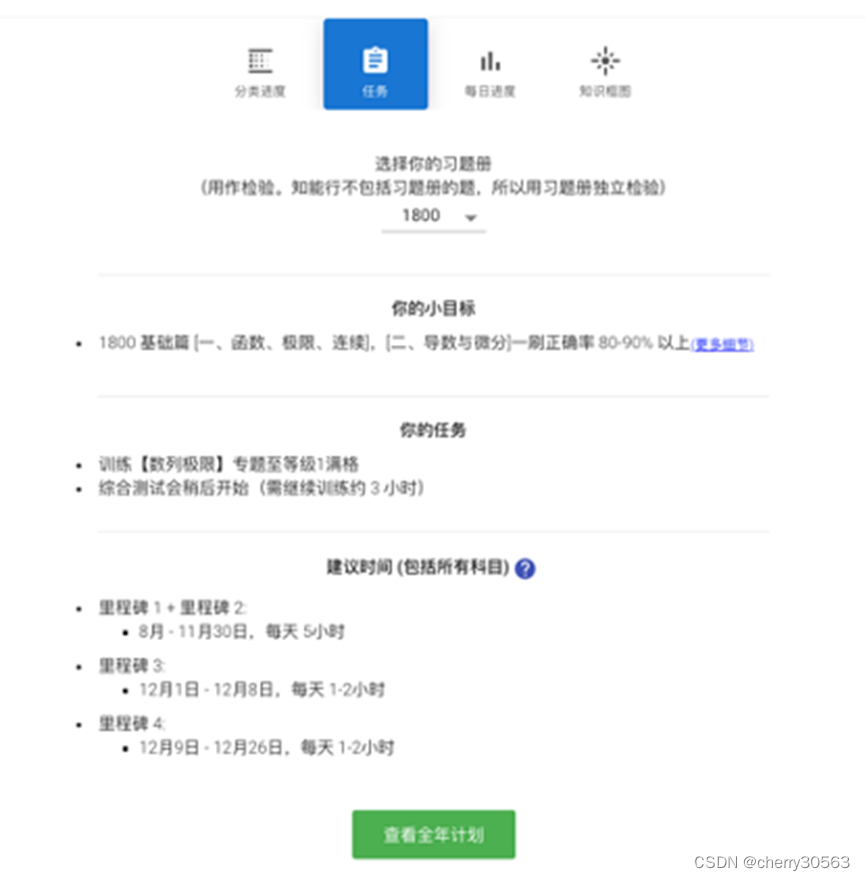
完成知能行的一个专题后,可以选择市面上的习题册(例如:1800题)来检验效果,通常一刷都可以达到80-90%的正确率。
基础阶段(3月-6月)
复习目标:复习基础知识点,培养计算能力
准备材料:市面上常见的基础复习辅导书都可以,可以开始使用知能行,争取将知能行的等级提升到2级
特别建议:基础较差的同学,遇到不懂的问题可以先观看视频课程,但一定要自己做题。
强化阶段(7月-9月)
复习目标:通过大量的做题和总结归纳,加深对知识点的融会贯通,提高解题能力。
准备材料:选择一本题型覆盖全面且解析质量较高的习题集。如果你的知能行各个章节达到了三级,那么你就可以进行每天提供的综合训练了,强化结束,让知能行达到四级就非常不错了。
友情提醒:1. 多做题,多动手,不要只看不练。2. 注意总结归纳
冲刺阶段(10月-12月)
复习目标:通过真题和模拟训练,强化重点,突破难点,弥补不足,争取取得高分。
准备材料:近十年的真题和市面上口碑较好的模拟卷。在这个阶段可以使用知能行的错题回顾功能。回顾自己的错题和薄弱知识点。然后努力将知能行的水平提升到五级,这样你就无敌了。
模拟卷推荐原则:题目具有创新性,而创新方向又接近真题的出题风格。
线代部分的复习
完成高数基础后一般会开始线代复习,通常暑假2个月足够。
线代总共包括六个部分,分别是行列式、矩阵、向量、线性方程组、矩阵的特征值和特征向量、二次型。
其中前三个是基础,后三个是应用。如果想熟练运用,就必须把前三个章节的知识点牢固掌握。考研中,由于线代所占知识点非常少,通常只出1-2题,填空1题,大题则综合运用这六章内容。
线代计算量不如高数大,但概念性很强。我刚开始是用李永乐的讲义学习,但感觉很吃力,即使掌握了基本概念和知识点,但稍微复杂的题目就懵了。就是那种看了答案,然后再回过头做,还是懵。
在学习线性方程组这一章时,实在是搞不懂题目,我在b站上搜索视频花费了太多时间,而且里面的内容也不一定适合我。
后来刷了知能行,感觉就豁然开朗了,面对题目有了思路,而且能够做对。
我觉得可能是因为李永乐讲义前几章用到了后面的内容,而我后面又不熟悉,所以就搞混了,感到很吃力。我记得第一章行列式就用到了向量,我当时连向量和秩是什么都不记得了。
讲义上有些例题不错,但大多数和真题相比较起来,知能行则包含了所有的真题。后来我刷完知能行,回头再做讲义上的题,正确率相当高。
四、我的一些经验教训:
1. 避免盲目追进度
决不能盲目追求进度,重点在于及时复习,及时回顾知识点并做一些相关题目练习。
我们必须认识到数学学习需要长时间的连续性实践。当做题时遇到忘记的地方就查书,以做题为主,结束做题后及时复习前面的内容。这里不需要刷很多题,晚上抽出时间复习前面的笔记或教材,但一定要坚持下去。
2. 对经验贴的态度
少看经验贴,就像看爽文一样,每个人都想成为爽文主角,但别人的经验未必百分百适合你。
多看别人失败的地方。就像有句话说的那样,其实地上本没有路,走的人多了也便有了路,考研也是一样的道理。多留意前人踩过的坑,自己就能避免掉。
学习的本质在于不断迭代和优化。不断迭代就是不断重复,不断优化就是优化我们学习的流程。我们想要学得更轻松,就得学会不断优化自己的学习方法,然后在实践中不断改进。
3. 不要依赖答案
学习数学最忌讳的就是不动手。遇到错题或者不会做的题目看答案无可厚非,但要明白,看懂了答案,不代表能自己做出来。看答案的过程中,我们是跟着答案的思路走,大多数情况下无法联系到题目整体,也就无法理解出题人的考察重点是什么。
在遇到难题时,很多人会想直接看答案。根据情况来看答案,一是如果有思路但做不到最后一步,就花20分钟攻克这个题目,看完答案后再重新做一遍;还有就是完全无思路,那就花1-3分钟仔细看题目所给的条件,写下自己的想法或者对公式的变形,然后再看答案,看懂后再重新尝试。
五、最后的话
考研过程中充满不确定性,焦虑是家常便饭。实际上,每个人都一样,即便是大佬们也是从一开始就备受紧张,焦虑的原因各有不同:
a) 别人进度比自己快
b) 数学太难,感觉学不完、学不会,想要放弃
c) 非考研人对自己的影响,让自己左右为难,不知是继续工作还是考研
d) 学习太累,脑子都转不动了,但觉得学习计划还没完成,还得继续学
还有许多其他情况,在考研之路上,千万别担心他人已经走得多远,也不用在意他人的不看好。专心、专心、再专心!
当我们想要放弃,觉得太累了,可以放下书本,出去散散步,或者和朋友家人聊聊天,甚至可以小憩片刻,或者给自己来顿美餐。
面对困难,我们要有迎难而上的勇气,要有成竹在胸的定力,勇敢地选择适合自己的道路,理性地对待困难。
加油,考研er!那些你为了赶路而低头不语的日子,将成为照亮你未来的星星。
这篇关于【考研数学】660/880/1000/1800 使用手册的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






