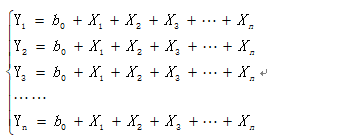本文主要是介绍多变量处理的LASSO方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.lasso方法
其中,因变量是Y,自变量是X。(数据中的变量众多,但如何选择X,就使用了lasso)
lasso能够对变量进行筛选和对模型的复杂程度进行降低。这里的变量筛选是指不把所有的变量都放入模型中进行拟合,而是有选择的把变量放入模型从而得到更好的性能参数。
lasso回归的特色就是在建立广义线型模型的时候,这里广义线型模型包含一维连续因变量、多维连续因变量、非负次数因变量、二元离散因变量、多元离散因变,除此之外,无论因变量是连续的还是离散的,lasso都能处理,总的来说,lasso对于数据的要求是极其低的,所以应用程度较广;除此之外,lasso还能够对变量进行筛选和对模型的复杂程度进行降低。这里的变量筛选是指不把所有的变量都放入模型中进行拟合,而是有选择的把变量放入模型从而得到更好的性能参数。 复杂度调整是指通过一系列参数控制模型的复杂度,从而避免过度拟合(Overfitting)。 对于线性模型来说,复杂度与模型的变量数有直接关系,变量数越多,模型复杂度就越高。 更多的变量在拟合时往往可以给出一个看似更好的模型,但是同时也面临过度拟合的危险
2.LASSO算法的优点
LASSO算法在模型系数绝对值之和小于某常数的条件下,谋求残差平方和最小,在变量选取方面的效果优于逐步回归、主成分回归、岭回归、偏最小二乘等,能较好的克服传统方法在模型选取上的不足。
这篇关于多变量处理的LASSO方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!