爬虫入门学习（三）请求headers处理

本文主要是介绍爬虫入门学习（三）请求headers处理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

有时候请求一个网页的时候，无论是GET请求还是POST请求都访问不了，并出现403错误。这是因为这些网页为了防止恶意采集信息，使用了反爬机制。

正文 

1、都什么原因会出现403错误呢？

403错误是指访问被服务器拒绝的错误。这可能是因为用户请求的资源被服务器禁止访问，或者用户没有足够的权限来访问资源。

有几个可能的原因导致403错误：

1. 权限不足：用户没有足够的权限来访问资源。这可能是因为用户没有提供正确的身份验证凭证，或者用户所属的用户组没有访问该资源的权限。

2. IP地址被拒绝：服务器可以配置为拒绝某些IP地址或IP地址范围的访问。

3. 文件或目录权限不正确：服务器上的文件或目录的权限设置不正确，导致用户无法访问。

2、如何发送GET请求？

import requests	# 导入requests模块
response = requests.get('https://www.csdn.net/?spm=1030.2210.3001.4476')

 3、如何发送POST请求？

import requests
response = requests.post("https://www.csdn.net/?spm=1030.2210.3001.4476")
print(response.content)

403了哈哈ha😀ha 

GET请求和POST请求的区别：

get请求是安全的。get请求是绝对安全的。因为get请求只是为了从服务器上获取数据。不会对服务器造成威胁。

post请求是危险的。因为post请求是向服务器提交数据，如果这些数据通过后门的方式进入到服务器当中，服务器是很危险的。另外post是为了提交数据，所以一般情况下拦截请求的时候，大部分会选择拦截（监听）post请求。

使用请求头部headers处理

1、打开浏览器

2、按下“Ctrl+Shift+E” 出现下面界面：

 3、点击蓝色的部分，找到头部信息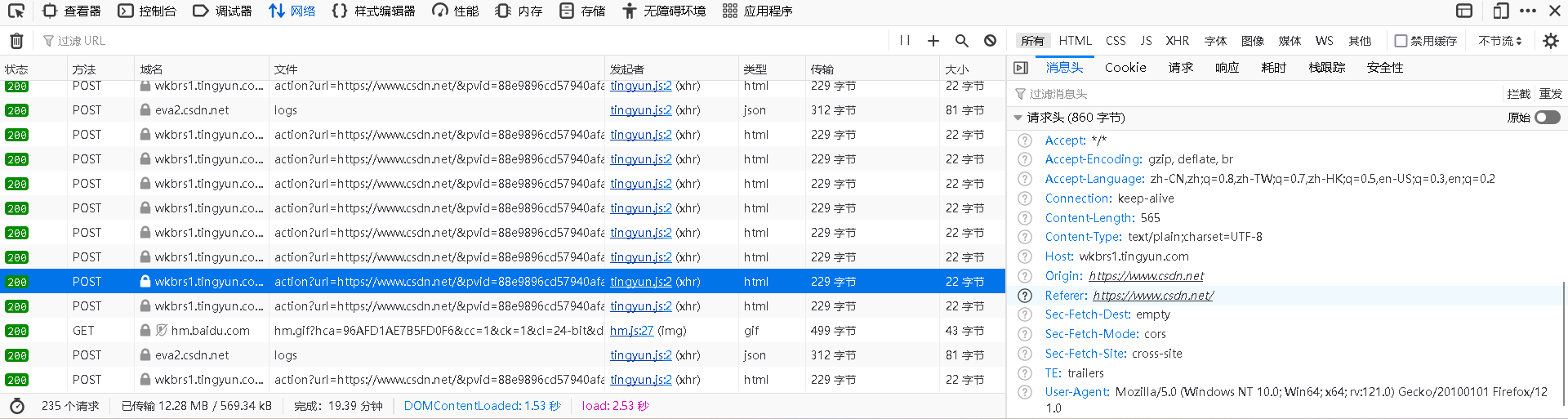

要的就是右下角的“'User-Agent':'Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:121.0) Gecko/20100101 Firefox/121.0'”

import requests# 请求的URL
url = 'https://www.csdn.net/?spm=1030.2210.3001.4476'
header = {'User-Agent':'Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:121.0) Gecko/20100101 Firefox/121.0'}
# 请求的数据
data = {'name': '后端'
}
# 发送POST请求
response = requests.post(url, data=data,headers=header)
# 打印响应内容
print(response.text)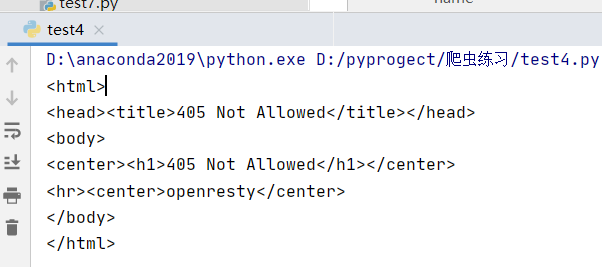

 

这回变成405了哈哈，所以我们得用GET了：

import requests# 请求的URL
url = 'https://www.csdn.net/?spm=1030.2210.3001.4476'
header = {'User-Agent':'Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:121.0) Gecko/20100101 Firefox/121.0'}
# 请求的数据
data = {'name': 'pp'
}
# 发送POST请求
response = requests.get(url, data=data,headers=header)
# 打印响应内容
print(response.text)

 

这篇关于爬虫入门学习（三）请求headers处理的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---