LSM与B+树的辨析

本文主要是介绍LSM与B+树的辨析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

LSM与B+树的辨析

LSM树与 B+树常常作为存储体系中的一种数据结构，所以他们之间也存在着相似性与不同之处， LSM树是在 B+树的基础上提出的，而 B+树是 B树(也称B-树)的扩展，所以我们按照递进的顺序来辨析其中的关系。

1. B树（B-树）

B树是一种平衡的多路查找树，它在文件系统中很有用，可以实现类似二叉排序树的查找。B树每个结点上是多关键码的有序表，在到达某个结点时，先在有序表中查找，若找到，则查找成功；否则，到按照对应的指针信息指向的子树中去查找，当到达叶子结点时，则说明树中没有对应的关键码。

一个m阶的B树具有如下几个特征：

1. 根结点至少有两个子女。

2. 每个中间节点都包含k-1个元素和k个孩子，其中 $m/2\le k\le m$

3. 每一个叶子节点都包含k-1个元素，其中 $m/2\le k\le m$

4. 所有的叶子结点都位于同一层。

5. 每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分。

以一个3阶B树为例：

$2\le k\le 3$
中间节点包含1-2个元素和2-3个孩子
叶子节点包含1-2个元素

2. B+树

B+树是应文件系统所需而产生的一种B树的变形树。传统关系型数据库使用B+树或一些变体作为存储结构，能高效进行查找。

一个m阶的B+树具有如下几个特征：

1. 根结点或者是叶子，或者至少有两棵子树，至多有m棵子树。
2. 除根节点外，所有非终端结点至少有 $[\frac{m}{2}]$ 棵子树，至多有m棵子树。
3. 所有叶结点在同一层次。
4. 若一个结点有n棵子树，则必含有n个关键字。
5. 所有叶子结点中包含了全部记录的关键字信息以及这些关键字记录的指针，而 且也结点按关键字大小从小到大顺序链接。
6. 所有非叶子结点可以看出是索引的部分，结点中只含有其子树的最大（或最小 ）关键字。

对比一下二者，我们可以看到二者的差异在于（B+树独有的）：

• 有n 棵子树的结点中含有n 个关键码
• 所有的叶子结点中包含了全部关键码的信息，及指向含有这些关键码记录的指针，且叶子结点本身依关键码的大小自小而大的顺序链接
• 所有的非叶子结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键码

以一个3阶B+树为例：

中间节点不保存数据，只是索引，数据都在叶节点。

3. LSM树

使用B+树或一些变体作为存储结构的传统关系型数据库虽然能高效进行查找。但保存在磁盘中时它也有一个明显的缺陷，那就是逻辑上相离很近但物理却可能相隔很远（中间节点是索引），这就可能造成大量的磁盘随机读写。

为了克服B+树的弱点，HBase引入了LSM树(Log-Structured Merge-Trees)的概念。

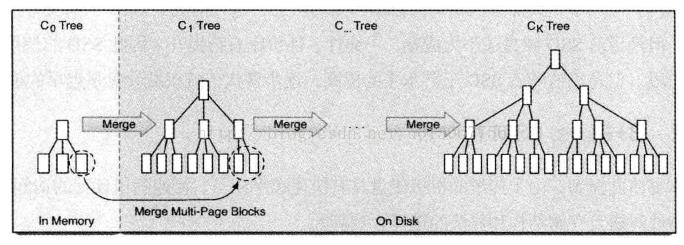
• LSM树是一种存储策略，可以采用任何已有的数据结构，如B+树。
• LSM树插入记录时，先写日志，然后在内存中插入，内存中的树称为C0树。
• 内存中的数据达到一定阈值，或经过一段时间间隔，C0树合并到磁盘C1中。
• C1中的数据可以进一步合并到C2中。
  

这篇关于LSM与B+树的辨析的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---