AVL树笔记（一）:zig-zag,insert,find,predecessor,successor

AVL树就是一棵平衡的二叉查找树。
其维护平衡的方式是：维护一个平衡因子h，即子树高度，如果左子树高度和右子树高度相差2，那么就旋转把它弄平衡。

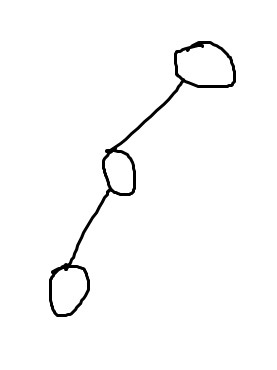
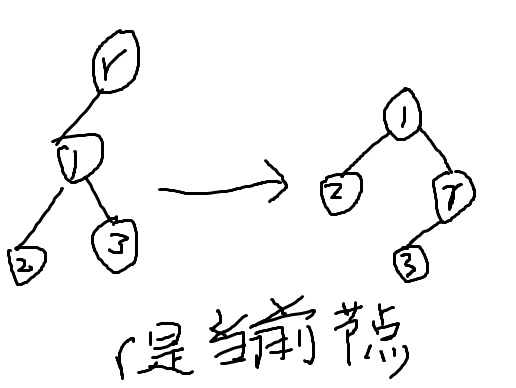
这个二叉树明显不平衡，可以发现全部左偏，于是右旋。
右旋就是当前节点的左儿子 的 右儿子是当前节点。
如果当前节点有右儿子，怎么办？
那么把这个右儿子拆下来然后装在当前节点的左儿子上。
如图：

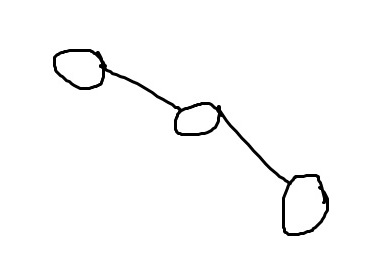
这个二叉树明显不平衡，可以发现全部右偏，于是左旋。
左旋就是当前节点的右儿子 的 左儿子是当前节点。
如果当前节点有左儿子，怎么办？
那么把这个左儿子拆下来然后装在当前节点的右儿子上。
这个不给图了。

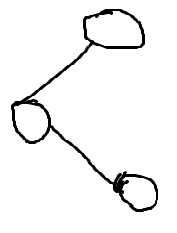
这个二叉树明显不平衡，下面右偏上面左偏，于是先左旋再右旋。

这个二叉树明显不平衡，下面左偏上面右偏，于是先右旋再左旋。
说白了就是全部反着来，是不是很好懂？
旋转完了，然后insert。
insert就是先插入进去，然后如果不平衡就旋转一下，就平衡了。
顺便更新h。
insert完了，然后find,predecessor,successor。
find,predecessor,successor就和二叉查找树一样。
明天讲讲delete。
附代码：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct node{int h,v,lc,rc;
}tree[40010];
int cnt,ans,n,val,pred,succ,rt;
int abs(int x)
{return x<0?-x:x;
}
int zig(int r)
{int t=tree[r].lc;tree[r].lc=tree[t].rc;tree[t].rc=r;tree[r].h=max(tree[tree[r].lc].h,tree[tree[r].rc].h)+1;tree[t].h=max(tree[tree[t].lc].h,tree[tree[t].rc].h)+1;return t;
}
int zag(int r)
{int t=tree[r].rc;tree[r].rc=tree[t].lc;tree[t].lc=r;tree[r].h=max(tree[tree[r].lc].h,tree[tree[r].rc].h)+1;tree[t].h=max(tree[tree[t].lc].h,tree[tree[t].rc].h)+1;return t;
}
int zigzag(int r)
{tree[r].rc=zig(tree[r].rc);return zag(r);
}
int zagzig(int r)
{tree[r].lc=zag(tree[r].lc);return zig(r);
}
int insert(int r,int x)
{if(r==0){tree[++cnt].v=x;tree[cnt].h=1;return cnt;}if(x<tree[r].v){tree[r].lc=insert(tree[r].lc,x);if(tree[tree[r].lc].h==tree[tree[r].rc].h+2){if(x<tree[tree[r].lc].v)r=zig(r);else if(x>tree[tree[r].lc].v)r=zagzig(r);}}else if(x>tree[r].v){tree[r].rc=insert(tree[r].rc,x);if(tree[tree[r].rc].h==tree[tree[r].lc].h+2){if(x>tree[tree[r].rc].v)r=zag(r);else if(x<tree[tree[r].rc].v)r=zigzag(r);}}tree[r].h=max(tree[tree[r].lc].h,tree[tree[r].rc].h)+1;return r;
}
bool find(int r,int x)
{if(r==0)return 0;if(tree[r].v==x)return 1;if(tree[r].v<x)return find(tree[r].rc,x);if(tree[r].v>x)return find(tree[r].lc,x);
}
void predecessor(int r,int x)
{if(r==0)return;if(tree[r].v<x){pred=tree[r].v;predecessor(tree[r].rc,x);}else predecessor(tree[r].lc,x);
}
void successor(int r,int x)
{if(r==0)return;if(tree[r].v>x){succ=tree[r].v;successor(tree[r].lc,x);}else successor(tree[r].rc,x);
}
int main()
{scanf("%d%d",&n,&ans);rt=insert(rt,-99999999);rt=insert(rt,99999999);rt=insert(rt,ans);for(int i=1;i<n;++i){scanf("%d",&val);if(find(rt,val))continue;pred=succ=0;predecessor(rt,val);successor(rt,val);ans+=min(abs(pred-val),abs(succ-val));rt=insert(rt,val);}printf("%d\n",ans);
}

这个题是BZOJ1588（HNOI2002）就是求前驱后继的裸题。