【智能算法】蝙蝠算法（BA)原理及实现

本文主要是介绍【智能算法】蝙蝠算法（BA)原理及实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

1.背景

2010年，Yang受到蝙蝠回声定位的特性启发，提出了蝙蝠算法(Bat Algorithm, BA)。

2.算法原理

2.1算法思想

蝙蝠算法模拟了蝙蝠利用回声定位系统寻找小型昆虫进行捕食的行为，主要分为速度位置更新和随机飞行。

2.2算法过程

速度位置更新：
$${\mathbf{v}}_i^t={\mathbf{v}}_i^{t-1}+({\mathbf{x}}_i^t-{\mathbf{x}}_{\ast })f_i$$
其中，$x_{\ast }$为最优个体位置，$f_i$为超声频率：
$$f_i=f_{\min }+(f_{\max }-f_{\min })\beta$$
位置更新：
$${\mathbf{x}}_i^t={\mathbf{x}}_i^{t-1}+{\mathbf{v}}_i^t$$
随机飞行：
随机生成一个数，蝙蝠根据是否大于脉冲频率进行随机飞行：
$${\mathbf{x}}_{\mathbf{new}}={\mathbf{x}}_{\mathbf{old}}+ϵA^t$$
伪代码：

3.代码实现

% 蝙蝠算法
function [Best_pos, Best_fitness, Iter_curve, History_pos, History_best]=BA(pop, maxIter, lb, ub, dim,fobj)
%input
%pop 种群数量
%dim 问题维数
%ub 变量上边界
%lb 变量下边界
%fobj 适应度函数
%maxIter 最大迭代次数
%output
%Best_pos 最优位置
%Best_fitness 最优适应度值
%Iter_curve 每代最优适应度值
%History_pos 每代种群位置
%History_best 每代最优个体位置
%% 控制参数
A=0.5;      % Loudness
r=0.5;      % Pulse rate
Qmin=0;         % Frequency minimum
Qmax=2;         % Frequency maximum
Q=zeros(pop,1);   % Frequency
v=zeros(pop,dim);   % Velocities
%% 初始化种群
for i=1:popSol(i,:)=lb+(ub-lb).*rand(1,dim);Fitness(i)=fobj(Sol(i,:));
end
% Find the initial best solution
[Best_fitness,I]=min(Fitness);
Best_pos=Sol(I,:);
%% 迭代
for t=1:maxIterfor i=1:pop% 速度&位置更新Q(i)=Qmin+(Qmin-Qmax)*rand;v(i,:)=v(i,:)+(Sol(i,:)-Best_pos)*Q(i);S(i,:)=Sol(i,:)+v(i,:);% 边界处理Sol(i,:)=simplebounds(Sol(i,:),lb,ub);% 随机飞行if rand>rS(i,:)=Best_pos+0.001*randn(1,dim);endFnew=fobj(S(i,:));if (Fnew<=Fitness(i)) & (rand<A)Sol(i,:)=S(i,:);Fitness(i)=Fnew;endif Fnew<=Best_fitnessBest_pos=S(i,:);Best_fitness=Fnew;endendIter_curve(t) = Best_fitness;History_best{t} = Best_pos;History_pos{t} = Sol;
end
end
function s=simplebounds(s,Lb,Ub)ns_tmp=s;I=ns_tmp<Lb;ns_tmp(I)=Lb(I);J=ns_tmp>Ub;ns_tmp(J)=Ub(J);s=ns_tmp;
end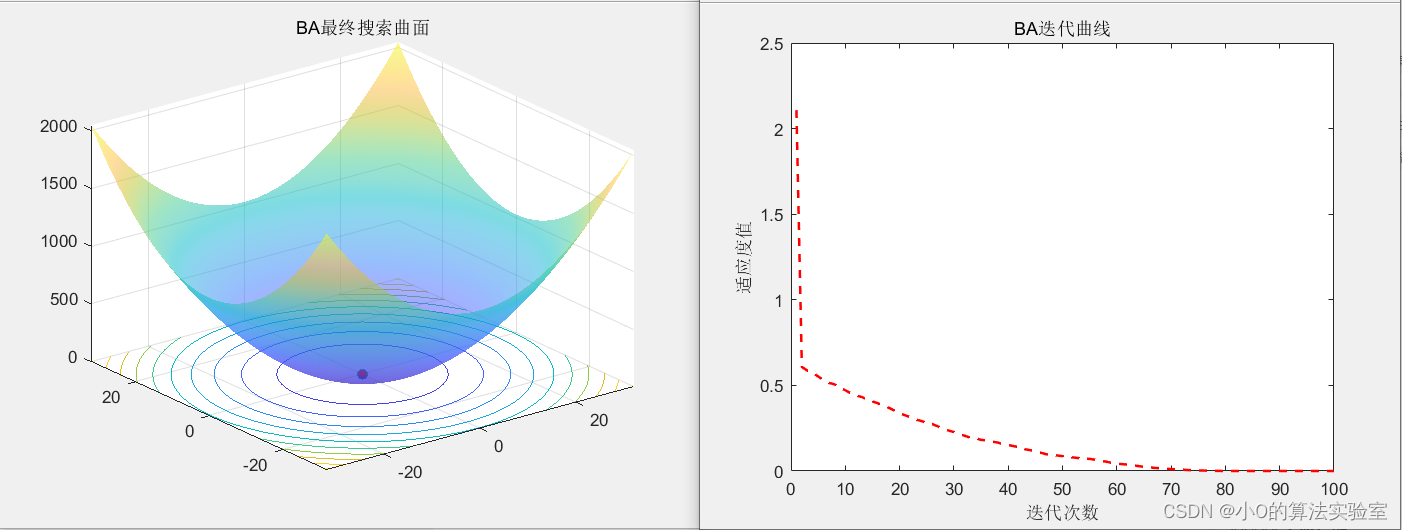

4.参考文献

[1] Yang X S. A new metaheuristic bat-inspired algorithm[M]//Nature inspired cooperative strategies for optimization (NICSO 2010). Berlin, Heidelberg: Springer Berlin Heidelberg, 2010: 65-74.

这篇关于【智能算法】蝙蝠算法（BA)原理及实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---